Í∑∏ÎûòÌîÑ(Graph)ÏôÄ Í∑∏ÎûòÌîÑ ÏïåÍ≥Ýζ¨Ï¶ò(Îã®Ïñ¥ÏǨÎã§Î¶¨ Ψ∏ÏÝú Ìï¥Í≤∞)
- 1. Í∑∏ÎûòÌîÑÏôÄ Í∑∏ÎûòÌîÑ ÏïåÍ≥Ýζ¨Ï¶ò (Graph & Graph Algorithm) Wider planet Tech Talk 2015.10.22 Ï°∞ÏùÄÏö∞
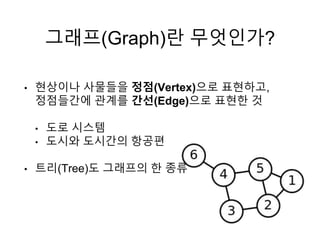
- 2. Í∑∏ÎûòÌîÑ(Graph)ÎûÄ Î¨¥ÏóáÏù∏Í∞Ä? ‚Ä¢ ÌòÑÏÉÅÏù¥ÎÇò ÏǨΨºÎì§ÏùÑ ÏÝïÏÝê(Vertex)ÏúºÎ°ú ÌëúÌòÑÌïòÍ≥Ý, ÏÝïÏÝêÎì§Í∞ÑÏóê Í¥ÄÍ≥ÑΕº Í∞ÑÏÑÝ(Edge)ÏúºÎ°ú ÌëúÌòÑÌïú Í≤É ‚Ä¢ ÎèÑΰú ÏãúÏä§ÌÖú ‚Ä¢ ÎèÑÏãúÏôÄ ÎèÑÏãúÍ∞ÑÏùò Ìï≠Í≥µÌé∏ ‚Ä¢ Ìä∏ζ¨(Tree)ÎèÑ Í∑∏ÎûòÌîÑÏùò Ìïú Ï¢ÖΕò
- 3. Í∑∏ÎûòÌîÑ Ïö©Ïñ¥(1) ‚Ä¢ ÏÝïÏÝê(Vertex) : ÏÝïÏÝê, ͺ≠ÏßÄÏÝê, ÎÖ∏ÎìúÎùºÍ≥ÝÎèÑ Î∂ÄΕ¥Î©∞, Í∑∏ÎûòÌîÑ ÏïåÍ≥Ýζ¨Ï¶òÏùò ÌïµÏ㨠‚Ä¢ Í∞ÑÏÑÝ(Edge) : ÏÝïÏÝêÎì§ Í∞ÑÏùò Í¥ÄÍ≥ÑΕº ÎÇòÌÉÄÎÉÑ. Í∞ÑÏÑÝÏù¥ Î∞©Ìñ•ÏùÑ Í∞ÄÏßÄΩ¥ ÏúÝÌñ• Í∑∏ÎûòÌîÑ(Directed Graph) ‚Ä¢ Í∞ÄϧëÏπò(Weight) : Ìïú ÏÝïÏÝêÏóêÏÑú Îã§Î•∏ ÏÝïÏÝêÏúºÎ°ú Í∞ÄÎäîÎç∞ Î∞úÏÉùÌïòÎäî ÎπÑÏö© ‚Ä¢ Í≤Ωΰú(Path) : Í∞ÑÏÑÝÏúºÎ°ú Ïó∞Í≤∞Îêú ÏÝïÏÝêÎì§ÏùÑ ÏàúÏÑúÎåÄΰú ÎÇòÏó¥Ìïú Í≤É ‚Ä¢ ÏàúÌôò(Cycle) : ÏúÝÌñ• Í∑∏ÎûòÌîÑÏóêÏÑú ÏàúÌôòÏùÄ ÏãúÏûë ÏÝïÏÝêÍ≥º ÎßàÏßÄÎßâ ÏÝïÏÝêÏù¥ Í∞ôÏùÄ Í≤Ωΰú. ÏàúÌôòÏù¥ ÏóÜÎäî Í∑∏ÎûòÌîÑÎäî Acyclic graph. ÏúÝÌñ•Í∑∏ÎûòÌîÑÍ∞Ä ÏàúÌôòÏùÑ Í∞ñÏßÄ ÏïäÏúºÎ©¥ Directed acyclic graph
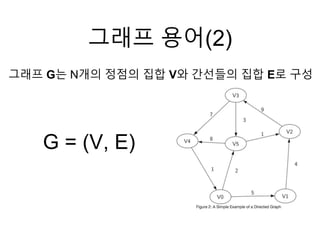
- 4. Í∑∏ÎûòÌîÑ Ïö©Ïñ¥(2) G = (V, E) Í∑∏ÎûòÌîÑ GÎäî NÍ∞úÏùò ÏÝïÏÝêÏùò ÏßëÌï© VÏôÄ Í∞ÑÏÑÝÎì§Ïùò ÏßëÌï© Eΰú ͵¨Ïѱ
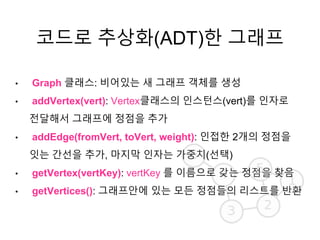
- 5. ÏΩîÎìúΰú Ï∂îÏÉÅÌôî(ADT)Ìïú Í∑∏ÎûòÌîÑ ‚Ä¢ Graph ÌÅ¥ÎûòÏä§: ÎπÑÏñ¥ÏûàÎäî ÏÉà Í∑∏ÎûòÌîÑ Í∞ùÏ≤¥Î•º ÏÉùÏѱ ‚Ä¢ addVertex(vert): VertexÌÅ¥ÎûòÏä§Ïùò Ïù∏Ïä§ÌÑ¥Ïä§(vert)Εº Ïù∏Ïûêΰú ÏÝÑÎã¨Ìï¥ÏÑú Í∑∏ÎûòÌîÑÏóê ÏÝïÏÝêÏùÑ Ï∂îÍ∞Ä ‚Ä¢ addEdge(fromVert, toVert, weight): Ïù∏ÏÝëÌïú 2Í∞úÏùò ÏÝïÏÝêÏùÑ ÏûáÎäî Í∞ÑÏÑÝÏùÑ Ï∂îÍ∞Ä, ÎßàÏßÄÎßâ Ïù∏ÏûêÎäî Í∞ÄϧëÏπò(ÏÑÝÌÉù) ‚Ä¢ getVertex(vertKey): vertKey Εº Ïù¥Î¶ÑÏúºÎ°ú Í∞ñÎäî ÏÝïÏÝêÏùÑ Ï∞æÏùå ‚Ä¢ getVertices(): Í∑∏ÎûòÌîÑÏïàÏóê ÏûàÎäî Ι®ÎìÝ ÏÝïÏÝêÎì§Ïùò ζ¨Ïä§Ìä∏Εº Î∞òÌôò
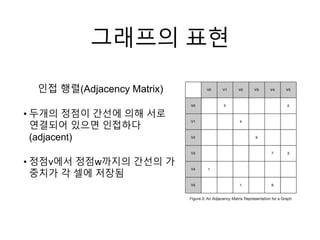
- 6. Í∑∏ÎûòÌîÑÏùò ÌëúÌòÑ Ïù∏ÏÝë ÌñâÎݨ(Adjacency Matrix) ‚Ä¢ ÎëêÍ∞úÏùò ÏÝïÏÝêÏù¥ Í∞ÑÏÑÝÏóê ÏùòÌï¥ ÏÑúΰú Ïó∞Í≤∞ÎêòÏñ¥ ÏûàÏúºÎ©¥ Ïù∏ÏÝëÌïòÎ㧠(adjacent) ‚Ä¢ ÏÝïÏÝêvÏóêÏÑú ÏÝïÏÝêwÍπåÏßÄÏùò Í∞ÑÏÑÝÏùò Í∞Ä Ï§ëÏπòÍ∞Ä Í∞Å ÏÖÄÏóê ÏÝÄÏû•Îê®
- 7. Í∑∏ÎûòÌîÑÏùò ÌëúÌòÑ Ïù∏ÏÝë ζ¨Ïä§Ìä∏(Adjacency List) ‚Ä¢ Í∑∏ÎûòÌîÑÏùò Ι®ÎìÝ ÏÝïÏÝêÏùÑ Í∏∞Ï§Ä Î¶¨Ïä§Ìä∏ ΰú ÏúÝÏßÄÌïòÍ≥Ý, Í∞Å ÏÝïÏÝêÎì§ÎßàÎ㧠Ïù∏ÏÝë Ìïú ÏÝïÏÝêÎì§ÏùÑ Î¶¨Ïä§Ìä∏ΰú Ïó∞Í≤∞ ‚Ä¢ Ïù∏ÏÝëÌñâÎݨÍ≥º Îã¨Î¶¨ Ï°¥Ïû¨ÌïòÏßÄ ÏïäÎäî Í∞Ñ ÏÑÝÏùÄ ÌëúÌòÑÏÉÅÏóê ÎÇòÌÉÄÎÇòÏßÄ ÏïäÏùå
- 8. Ïù∏ÏÝë ÌñâÎݨ(Adjacency Matrix) Ïû•ÏÝê ‚Ä¢ Í∞ÑÎã®Ìï¥ÏÑú Ïù¥Ìï¥ÌïòÍ∏∞ Ïâ¨Ïö∞Ω∞, Í∞ÑÏÑÝÏùò Ï°¥Ïû¨Ïó¨Î∂ÄΕº ϶âÍ∞Å Ïïå Ïàò ÏûàÏùå ‚Ä¢ Î∞ÄÎèÑÍ∞Ä ÏïÑÏ£º ÎÜíÏùÄ Í∑∏ÎûòÌîÑΕº ÌëúÌòÑÌïòÍ∏∞Ïóê ÏÝÅÌï© Îã®ÏÝê ‚Ä¢ ÌñâÎݨÏùÑ Ï§ÄÎπÑÌïòÎäî Í≥ºÏÝïÏóêÏÑú ÏÝïÏÝêÏùò Í∞úÏàò(n)Ïùò ÏÝúÍ≥±ÎßåÌźÏùò Í≥µ Í∞ÑÍ≥º ÏãúÍ∞ÑÏù¥ ÌïÑÏöîÌï® ‚Ä¢ Î∞ÄÎèÑÍ∞Ä ÎÇÆÏùÄ Í∑∏ÎûòÌîÑÎäî Îπà Í≥µÍ∞ÑÏù¥ ÎßéÏù¥ ÏÉùÍ∏∞Í∏∞ ÎïåΨ∏Ïóê ÏÝÅÌï© ÌïòÏßÄ ÏïäÏùå
- 9. Ïù∏ÏÝë ζ¨Ïä§Ìä∏(Adjacency List) Ïû•ÏÝê ‚Ä¢ Í≥µÍ∞ÑÏù¥ Í∞ÑÏÑÝÏùò Ï¥ù Í∞úÏàòÏóê ÎπÑΰÄÌïòÎäî ÏñëÎßåÌźÎßå ÌïÑÏöîÌïòÎØÄΰú ÎÇ≠ÎπÑÍ∞Ä ÏóÜÏùå ‚Ä¢ Î∞ÄÎèÑÍ∞Ä ÎÇÆÏùÄ Í∑∏ÎûòÌîÑΕº ÌëúÌòÑÌïòÎäîÎç∞ ÏÝÅÌï© ‚Ä¢ ÌäπÏÝï ÏÝïÏÝêÏùÑ Í∏∞ϧÄÏúºÎ°ú Ïó∞Í≤∞ÎêòÏñ¥ ÏûàÎäî Ι®ÎìÝ Í∞ÑÏÑÝÏùÑ ÏâΩÍ≤å Ï∞æÏùÑ Ïàò ÏûàÏùå Îã®ÏÝê ‚Ä¢ Ι®ÎìÝ ÏÝïÏÝêÏóê Í∞ÑÏÑÝÏù¥ Ï°¥Ïû¨ÌïòÎäî Í≤ΩÏö∞ ζ¨Ïä§Ìä∏Εº ÎßåÎìúÎäîÎç∞ ÎßéÏùÄ ÎπÑÏö©Ïù¥ Î∞úÏÉù ‚Ä¢ ÏÝïÏÝêÎì§Í∞ÑÏóê Í∞ÑÏÑÝÏùò ÏúÝΨ¥Î•º ÌôïÏù∏ÌïòÍ∏∞ ÏúÑÌï¥ Î¶¨Ïä§Ìä∏Εº Ï∞®Î°Äΰú ÌõìÏñ¥ÏïºÌï®
- 10. <?php class Vertex { public function __construct($key) { $this->id = $key; $this->connect_to = array(); } public function addNeighbor($neighbor, $weight = 0) { $this->connect_to[$neighbor->getId()] = array('neighbor' => $neighbor, 'weight' => $weight); } public function getConnections() { return array_keys($this->connect_to); } public function getId() { return $this->id; } public function getWeight($neighbor) { return $this->connect_to[$neighbor->getId()]['weight']; } } PHP ÌÅ¥ÎûòÏä§Î°ú ÏÝïÏÝêÏùò Ïù∏ÏÝë ζ¨Ïä§Ìä∏ ͵¨ÌòÑ 4 5 3 6
- 11. Îã®Ïñ¥ ÏǨÎã§Î¶¨ Ψ∏ÏÝú (The Word Ladder Problem) ‚Ä¢ ‚ÄòÏù¥ÏÉÅÌïú ÎÇòÎùºÏùò Ïóòζ¨Ï䧂ÄôÏùò ÏûëÍ∞Ä ‚ÄòΣ®Ïù¥Ïä§Ï∫êÎü¥‚Äô Î∞ú명 ‚Ä¢ ÏãúÏûë Îã®Ïñ¥ÏóêÏÑú ÎèÑÏ∞© Îã®Ïñ¥ÍπåÏßÄ ÌïúÍ∏ÄÏûêÏî© Î∞îÍøî Í∞ÄΩ¥ÏÑú ÎèÑÎ㨠‚Ä¢ Í∞Å Îã®Í≥ÑÎßàÎ㧠Ι®Îëê ÏùòÎØ∏Í∞Ä ÏûàÎäî Îã®Ïñ¥Í∞Ä ÎêòÏñ¥Ïïº Ìï®
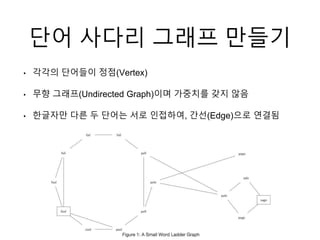
- 12. Îã®Ïñ¥ ÏǨÎã§Î¶¨ Í∑∏ÎûòÌîÑ ÎßåÎì§Í∏∞ ‚Ä¢ Í∞ÅÍ∞ÅÏùò Îã®Ïñ¥Îì§Ïù¥ ÏÝïÏÝê(Vertex) ‚Ä¢ Ψ¥Ìñ• Í∑∏ÎûòÌîÑ(Undirected Graph)Ïù¥Î©∞ Í∞ÄϧëÏπòΕº Í∞ñÏßÄ ÏïäÏùå ‚Ä¢ ÌïúÍ∏ÄÏûêÎßå Îã§Î•∏ Îëê Îã®Ïñ¥Îäî ÏÑúΰú Ïù∏ÏÝëÌïòÏó¨, Í∞ÑÏÑÝ(Edge)ÏúºÎ°ú Ïó∞Í≤∞Îê®
- 13. Îã®Ïñ¥ ÏǨÎã§Î¶¨ Í∑∏ÎûòÌîÑ Íµ¨ÌòÑ 1. Ι®ÎìÝ ÏÝïÏÝêÎì§ÎßàÎ㧠Îã§Î•∏ ÏÝïÏÝêÍ≥º ÎπÑ교 • Îã®ÏÝê: ÎπÑ͵êÌïòÎäî ÌöüÏàòÎäî Îã®Ïñ¥ Í∞úÏàòÏóê ÏÝúÍ≥± 2. Îã®Ïñ¥Ïùò ÌïúÍ∏ÄÏûêÎßå Í∞Äζ∞ ÎùºÎ≤®ÏùÑ Îã® Îã®Ïñ¥ Î≤ÑϺìÏùÑ ÎßåÎì§Ïñ¥ Îã®Ïñ¥Îì§ ÏùÑ Î∂ÑΕò
- 14. 단어 사다리 그래프 구현<?php require_once('Graph.php'); function buildGraph($word_file) { $container = array(); $graph = new Graph(); $f = fopen($word_file, "r"); if ($f) { while (($word = fgets($f)) !== false) { $container = setBucketContainer(trim($word)); } fclose($f); } else { throw new Exception('파일을 읽을 수 없습니다.'); } $bucket_keys = array_keys($container); foreach ($bucket_keys as $bucket) { foreach ($container[$bucket] as $word1) { foreach ($container[$bucket] as $word2) { if ($word1 != $word2) { $graph->addEdge($word1, $word2); } } } } return $graph; }
- 15. 단어 사다리 그래프 구현(2) function setBucketContainer($word) { $container = array(); $word_length = strlen($word); for ($i = 0; $i < $word_length; $i++) { $bucket = substr($word, 0, $i) . '_' . substr($word, $i + 1, ($word_length - 1) - $i); if (array_key_exists($bucket, $container)) { array_push($container[$bucket], $word); } else { $container[$bucket] = array($word); } } return $container; }
- 16. ÎÑàÎπÑ Ïö∞ÏÑÝ ÌÉêÏÉâ (Breath First Search) ‚Ä¢ ÌÉêÏÉâÍ≥ºÏÝïÏùÑ Ìä∏ζ¨Î°ú ÌëúÌòÑÌïòΩ¥ Ïù¥Ìï¥ÌïòÍ∏∞ Ïâ¨ÏõÄ ‚Ä¢ Σ®Ìä∏(root)ÎÖ∏ÎìúΕº ÏãúÏûëÏúºÎ°ú Í∞ôÏùÄ Í±∞ζ¨Ïóê ÏûàÎäî ÏûêÏãù ÎÖ∏ÎìúÎì§ÏùÑ ÌÉêÏÉ⠂Ģ Î∂ÄΙ® ÎÖ∏ÎìúÎäî ÏûêÏãù ÎÖ∏ÎìúÎì§ÏùÄ ÏÝÑÏûÑÏûê(Predecessor)ΰú Îì±Î°ùÌïòÍ≥Ý, ÌòÑÏû¨ÍπåÏßÄÏùò ÎàÑÏÝŠͱ∞ζ¨Î•º ÏÝÄÏû•
- 17. ÎÑàÎπÑÏö∞ÏÑÝÌÉêÏÉâ(BFS) ͵¨ÌòÑfunction bfs($start_vertex) { $start_vertex->setDistance(0); $start_vertex->setPredcessor(false); $queue = array(); array_push($queue, $start_vertex); while (count($queue) > 0) { $current_vertext = array_shift($queue); $neighbor = $current_vertext->getConnections(); foreach ($neighbor as $nbr_vertext) { if ($nbr_vertext['neighbor']->getColor() == 'white') { $nbr_vertext['neighbor']->setColor('gray'); $nbr_vertext['neighbor']->setDistance($current_vertext->getDistance() + 1); $nbr_vertext['neighbor']->setPredecessor($current_vertext); array_push($queue, $nbr_vertext['neighbor']); } } $current_vertext->setColor('black'); } } bfs($word_radder->getVertex('fool'));
- 18. Github $ git clone https://github.com/jonnung/word_ladder_graph
- 19. Í∞êÏǨ«Í©ÎãàÎã§.
Editor's Notes
- #3: Ïñ¥Îñ§ ÌòÑÏÉÅÏù¥ÎÇò ÏǨΨºÎì§Í∞ÑÏóê Í¥ÄÍ≥ÑΕº ÌëúÌòÑÌïÝÎïå ÏÝïÏÝêÍ≥º ÏÝïÏÝêÎì§ ÏǨÏù¥Î•º ÏûáÎäî Í∞ÑÏÑÝÏúºÎ°ú ÌëúÌòÑÌïòÎäî ÏûêΣå͵¨Ï°∞Εº 'Í∑∏ÎûòÌîÑ'ÎùºÍ≥Ý Ìï©ÎãàÎã§. Ïã§ÏÉùÌôúÏóêÏÑú Í∑∏ÎûòÌîÑΰú ÌëúÌòÑÌïÝ Ïàò ÏûàÎäî ÏÉÅÌô©ÏùÄ 'ÎèÑΰú ÏãúÏä§ÌÖú', 'Ìï≠Í≥µÌé∏', 'Ïù∏ÌÑ∞ÎÑ∑ Ïó∞Í≤∞'Îì±Ïù¥ ÏûàÍ≤ÝÏäµÎãàÎã§. ÌòÑÏû¨ Î≥¥ÏãúÎäî Ïä¨ÎùºÏù¥ÎìúÏóê ÏûàÎäî ÏûëÏùÄ Í∑∏ÎûòÌîÑ Í∑∏ζºÍ≥º ÏúÑ Ïã§ÏÉùÌôú ÏòàΕº Ìï®Íªò ÏÉùÍ∞ÅÌï¥Î≥¥Î©¥ Î∞îΰú Ïù¥Ìï¥Í∞Ä Í∞ÄÏ㧠Í≤ÉÏûÖÎãàÎã§. ÏßÄÎÇú ÏÑπÏÖòÏóê 'Ï°∞ÏÝïÌù¨'ÎãòÏù¥ Î∞úÌëú Ìï¥Ï£ºÏãÝ Ìä∏ζ¨ÎèÑ Í∑∏ÎûòÌîÑÏùò Ìïú Ï¢ÖΕò ÏûÖÎãàÎã§. Ï∞®Ïù¥ÏÝêÏù¥ ÏûàÎã§Î©¥ Ìä∏ζ¨Îäî ÏûêΣåÎì§Í∞ÑÏóê Í≥ÑÏ∏µ Í¥ÄÍ≥ÑΕº ÌëúÌòÑÌïòÍ∏∞ ÏúÑÌïú Í≤ÉÏù¥Í≥Ý, Í∑∏ÎûòÌîÑÎäî ÏõêÏÜåÎì§Í∞ÑÏóê Í¥ÄÍ≥ÑΕº ÌëúÌòÑÌïòÍ∏∞ ÏúÑÌïú ÏûêΣå ͵¨Ï°∞ÏûÖÎãàÎã§.¬Ý Î∞îΰú Îí§Ïóê Ïö©Ïñ¥ ÏѧΙÖÏóêÏÑú ÎÇòÏò§ÏßÄÎßå Í∑∏ÎûòÌîÑÎßåÏù¥ ÏàúÌôò Ïù¥ÎùºÎäî ͵¨Ï°∞Εº Í∞ñÍ≥Ý ÏûàÏùÑ Ïàò ÏûàÏäµÎãàÎã§.
- #7: Ϫ¥Ìì®ÌÑ∞ÏóêÏÑú Í∑∏ÎûòÌîÑΕº ÌëúÌòÑÌïòÎäî Î∞©Î≤ïÏùÑ ÏïåÏïÑÎ≥¥Í≤ÝÏäµÎãàÎã§. Í∑∏ÎûòÌîÑ ÌëúÌòÑÎ≤ïÏóêÎäî ÌŨÍ≤å ÌñâÎݨÏùÑ Ïù¥Ïö©ÌïòÎäî Î∞©Î≤ïÍ≥º ζ¨Ïä§Ìä∏Εº Ïù¥Ïö©ÌïòÎäî Î∞©Î≤ïÏù¥ ÏûàÏäµÎãàÎã§. Í∑∏ϧëÏóêÏÑú Í∞ÄÏû• Ïâ¨Ïö¥ Î∞©Î≤ïϧëÏóê ÌïòÎÇòÏù∏ Ïù∏ÏÝëÌñâÎݨÏùÑ Ïù¥Ïö©ÌïòÎäî Î∞©Î≤ïÏûÖÎãàÎã§. Í∑∏ÎûòÌîÑÏùò Ι®ÎìÝ ÏÝïÏÝêÎì§ÏùÄ ÌñâÎݨÏùò ÌñâÍ≥º Ïó¥Î°ú ÌëúÌòÑÎêòÎäîÎç∞Ïöî, ÏÝïÏÝê v0 ÏóêÏÑú ÏÝïÏÝêv1ÍπåÏßÄÏùò Í∞ÑÏÑÝÏùÄ Ìñâv0Í≥º Ïó¥v1Ïù¥ ͵êÏ∞®ÎêòÎäî ÏÖÄÏóê Í∞ÄϧëÏπò 5Í∞Ä ÏÝÄÏû•ÎêòÎäî Í≤ÉÏûÖÎãàÎã§.
- #8: Ïù∏ÏÝëζ¨Ïä§Ìä∏Îäî Í∞Å ÏÝïÏÝêÏóê Ïù∏ÏÝëÌïú ÏÝïÏÝêÎì§ÏùÑ Î¶¨Ïä§Ìä∏ΰú ÌëúÌòÑÌïòÎäî Î∞©Î≤ï ÏûÖÎãàÎã§. Í∑∏ÎûòÌîÑÏùò Ι®ÎìÝ ÏÝïÏÝêÏùÑ Í∏∞Ï§Ä Î¶¨Ïä§Ìä∏ΰú ÏúÝÏßÄÌïòÍ≥Ý, Í∞Å ÏÝïÏÝêÎì§ÎßàÎ㧠Ïù∏ÏÝëÌïú ÏÝïÏÝêÎì§ÏùÑ Î¶¨Ïä§Ìä∏ΰú Ïó∞Í≤∞Ìï©ÎãàÎã§. Ïù∏ÏÝëÌñâÎݨÍ≥º Îã¨Î¶¨ Ï°¥Ïû¨ÌïòÏßÄ ÏïäÎäî Í∞ÑÏÑÝÏùÄ ÎãπÏó∞Ìûà ζ¨Ïä§Ìä∏ΰú ÌëúÌòÑÎêòÏßÄ ÏïäÏäµÎãàÎã§.
- #9: Ïù∏ÏÝë ÌñâÎݨÏùò Ïû•ÏÝêÏùÄ Í∞ÑÎã®Ìï¥ÏÑú Ïù¥Ìï¥ÌïòÍ∏∞ Ïâ¨Ïö∞Ω∞, ÎÖ∏ÎìúÏôÄ ÎÖ∏ÎìúÍ∞ÑÏóê Ι®ÎìÝ Ïó∞Í≤∞ÏùÑ ÌïúÎààÏóê ÏâΩÍ≤å ÏïåÏïÑÎ≥º Ïàò ÏûàÏäµÎãàÎã§. ÌïòÏßÄÎßå ÌñâÎݨÏùÑ Ï§ÄÎπÑÌïòÍ∏∞ ÏúÑÌï¥ ÏÝïÏÝêÏùò Í∞úÏàòÏùò ÏÝúÍ≥±Ïóê Ìï¥ÎãπÌïòÎäî ÌñâÎݨÏù¥ ÌïÑÏöîÌïòΩ∞, Í∑∏ÎßåÌźÏùò ÏãúÍ∞ÑÎèÑ ÌïÑÏöîÌï©ÎãàÎã§. Í∑∏ζ¨Í≥Ý Í∞ÑÏÑÝÏùò Í∞úÏàòÍ∞Ä ÏÝÅÏùÄ, ϶â Î∞ÄÎèÑÍ∞Ä ÎÇÆÏùÄ Í∑∏ÎûòÌîÑΕº Ïù∏ÏÝëÌñâÎݨΰú ÌëúÌòÑÌïòΩ¥ ÎπàÍ≥µÍ∞ÑÏù¥ ÎßéÏù¥ ÏÉùÍ∏∞Í≤å Îê©ÎãàÎã§. ÏòàΕºÎì§Ïñ¥ 100ÎßåÍ∞úÏùò ÏÝïÏÝêÏùÑ ÏÝïÏÝêÏùÑ Í∞ÄÏßÑ Í∑∏ÎûòÌîÑÍ∞Ä 200ÎßåÍ∞úÏùò Í∞ÑÏÑÝÏùÑ Í∞ñÎäîÎã§Î©¥ ÌñâÎݨÏùò Ï¥ù ÏÖÄÏùÄ 1Ï°∞Í∞úÍ∞Ä ÎêòÏßÄÎßå Í≥ÝÏûë 200ÎßåÍ∞úÏùò ÏÖÄÏóêÎßå Í∞ÄϧëÏπò Í∞íÏù¥ ϱÑÏõåÏßÄÍ∏∞ ÎïåΨ∏Ïóê Í≥µÍ∞Ñ ÎÇ≠ÎπÑÍ∞Ä Ïã¨Ìï©ÎãàÎã§. Îî∞ÎùºÏÑú Ïù∏ÏÝëÌñâÎݨÏùÄ Î∞ÄÎèÑÍ∞Ä ÏïÑÏ£º ÎÜíÏùÄ Í∑∏ÎûòÌîÑΕº ÌëúÌòÑÌïòÍ∏∞Ïóê ÏÝÅÌï©Ìï©ÎãàÎã§.
- #10: Ïù∏ÏÝëÌñâÎݨÍ≥º Î∞òÎåÄΰú Ï°¥Ïû¨ÌïòÎäî Í∞ÑÏÑÝÎßå ζ¨Ïä§Ìä∏ΰú ÌëúÌòÑÎêòÍ∏∞ ÎïåΨ∏Ïóê Í≥µÍ∞ÑÎÇ≠ÎπÑÍ∞Ä ÏóÜÏäµÎãàÎã§. Îî∞ÎùºÏÑú Î∞ÄÎèÑÍ∞Ä ÎÇÆÏùÄ Í∑∏ÎûòÌîÑΕº ÌëúÌòÑÌïòÎäîÎç∞ ÏÝÅÌï©ÌïòÎã§Í≥Ý ÌïÝ Ïàò ÏûàÏäµÎãàÎã§.¬Ý Í∑∏ζ¨Í≥Ý Ïù∏ÏÝëÌñâÎݨÏù¥ ÏÝÑÏ≤¥ÏÝÅÏù∏ Í¥ÄÍ≥ÑΕº ÏÇ¥Ìé¥Î≥¥Í∏∞ Ïö©Ïù¥ ÌïòÎã§Î©¥ Ïù∏ÏÝëζ¨Ïä§Ìä∏Îäî ÌäπÏÝï ÏÝïÏÝêÏùÑ ÎåÄÏÉÅÏúºÎ°ú Ïó∞Í≤∞Îêú Ι®ÎìÝ Í∞ÑÏÑÝÏùÑ ÏâΩÍ≤å Ï∞æÏïÑÎ≥º Ïàò ÏûàÎã§Îäî Ï∏°Î©¥Ïù¥ ÏûàÏäµÎãàÎã§. ÌïòÏßÄÎßå Î∞ÄÎèÑÍ∞Ä ÎÜíÏùÄ Í∑∏ÎûòÌîÑÏùò Í≤ΩÏö∞ Ïù¥Îü∞ Î∂ÄÎ∂ÑÎèÑ Îã®ÏÝêÏúºÎ°ú ÏûëÏö©ÌïòÎäîÎç∞Ïöî. ÏÝïÏÝêÎì§Í∞ÑÏóê Í∞ÑÏÑÝÏùò ÏúÝΨ¥Î•º ÌôïÏù∏ÌïòÍ∏∞ ÏúÑÌï¥ Î¶¨Ïä§Ìä∏Εº Ï≠â ÌõìÏñ¥Ïïº ÌïúÎã§Îäî Îã®ÏÝêÏù¥ ÏûàÏäµÎãàÎã§.
- #13: Í∑∏ÎûòÌîÑΰú Îã®Ïñ¥Í∞ÑÏùò Í¥ÄÍ≥ÑΕº ÌëúÌòÑ Ìï¥Î≥¥Í≤ÝÏäµÎãàÎã§. Îã®Ïñ¥ ÏǨÎã§Î¶¨ Í∑∏ÎûòÌîÑÎäî Í∞ÅÍ∞ÅÏùò Îã®Ïñ¥Îäî ÏÝïÏÝêÏù¥ Îê©ÎãàÎã§. Í∑∏ζ¨Í≥Ý ÏÝïÏÝêÎì§ ÏǨÏù¥Ïóê Í∞ÑÏÑÝÏùÄ Î∞©Ìñ•ÏùÑ Í∞ñÏßÄ ÏïäÎäî Ψ¥Ìñ• Í∑∏ÎûòÌîÑ ÏûÖÎãàÎã§. Í∑∏ζ¨Í≥Ý Í∞ÄϧëÏπòÎèÑ Í∞ñÏßÄ ÏïäÏäµÎãàÎã§. Îã®Ïñ¥Í∞ÑÏóê Í∞ÑÏÑÝÏùÄ ÏÑúΰú ÌïúÍ∏ÄÏûêÏî© Îã§Î•¥Î©¥ Ïù∏ÏÝëÌïòÎã§Í≥Ý ÌïÝ Ïàò ÏûàÏäµÎãàÎã§.
- #14: Ïù¥ Ψ∏ÏÝúΕº Ìï¥Í≤∞ÌïòÍ∏∞ ÏúÑÌï¥ Í∞ÄÏû• ήºÏÝÄ ÎñÝÏò¨Î¶¥ Ïàò ÏûàÎäî Î∞©Î≤ïÏùÄ Í∞Å ÏÝïÏÝêÎßàÎ㧠Îã§Î•∏ ÏÝïÏÝêÍ≥º Ι®Îëê ÎπÑ͵êÌïòÎäî Í≤É ÏûÖÎãàÎã§. ÌïòÏßÄÎßå Îã®Ïñ¥Ïùò Í∞úÏàòÍ∞Ä ÏóÑÏ≤≠ ÎßéÎã§Î©¥ Ïù¥ Î∞©Î≤ïÎèÑ ÎßéÏùÄ Î∂ÄÌïòΕº Ï£ºÍ≤å Îê©ÎãàÎã§. Îòê ÌïúÍ∞ÄÏßÄ Î∞©Î≤ïÏùÄ Îã®Ïñ¥Ïùò ÌïúÍ∏ÄÏûêÎßå Ïñ∏ÎçîÎ∞îΰú Í∞Äζ∞ ÎùºÎ≤®ÏùÑ Í∞ÄÏßÑ ÌÅ∞ Îã®Ïñ¥ Î≤ÑϺìÏùÑ ÎßåÎì§Ïñ¥ Îã®Ïñ¥Îì§ÏùÑ Î∂ÑΕòÌïú ÌõÑ Ï∞®Î°ÄÏ∞®Î°Ä ÎπÑ͵êÌïòÎäî Í≤ÉÏûÖÎãàÎã§. Ïù¥Í≤ÉÏùÑ ÏΩîÎìúΰú ͵¨ÌòÑÌï¥ Î≥¥ÎèÑΰù ÌïòÍ≤ÝÏäµÎãàÎã§.
- #15: ÌïúϧÑÏóê ÌïúÍ∞úÏùò Îã®Ïñ¥Í∞Ä ÏûàÎäî ÌååÏùºÏùÑ ÌïúϧÑÏî© ÏùΩÏñ¥Îì§ÏûÖÎãàÎã§. Îã®Ïñ¥ ÏǨÎã§Î¶¨Ïùò ÏǨÏÝÑ Ï°∞ͱ¥ÎåÄΰú Ι®ÎìÝ Îã®Ïñ¥Ïùò Í∏ÄÏûêÏàòÎäî Í∞ôÏäµÎãàÎã§.¬Ý Îã®Ïñ¥Ïùò Ï≤´Í∏ÄÏûêÎ∂ÄÌÑ∞ ÏàúÏÑúÎåÄΰú Î∏îÎùºÏù∏Îìú, ϶â Ïñ∏ÎçîÎ∞îΰú ÏπòÌôòÌïú Ψ∏ÏûêΕº Ìǧ(key)ΰú ÏǨÏö©Ìï©ÎãàÎã§. Í∑∏ ÌǧΕº Ϫ®ÌÖåÏù¥ÎÑà Î∞∞Ïó¥ Î≥ÄÏàòÏùò Ìǧΰú Îã®Ïñ¥Î•º Ï∂îÍ∞Ä Ìï©ÎãàÎã§. Ι®ÎìÝ Îã®Ïñ¥Í∞Ä Î≤ÑϺìÏúºÎ°ú Î∂Ñζ¨Îêú Ϫ®ÌÖåÏù¥ÎÑàÏóê ÏÝÄÏû•Ïù¥ ÎêòΩ¥, Ïù¥ÏÝú Ìï¥Îãπ Î≤ÑϺìÎì§ÏùÑ ÌïòÎÇòÏî© Îí§ÏÝ∏Í∞ÄΩ∞ Í∑∏ÎûòÌîÑ Í∞ùÏ≤¥Ïùò Í∞ÑÏÑÝÏúºÎ°ú Ï∂îÍ∞ÄÌï©ÎãàÎã§.
- #17: Ïù¥ÏÝú ÎßåÎì§Ïñ¥ÏßÑ Í∑∏ÎûòÌîÑΕº Î≥∏Í≤©ÏÝÅÏúºÎ°ú ÌÉêÏÉâÌïòÎäî Í∑∏ÎûòÌîÑ ÏïåÍ≥Ýζ¨Ï¶òÏùÑ ÏïåÏïÑÎ≥¥ÎèÑΰù ÌïòÍ≤ÝÏäµÎãàÎã§. ÎÑàÎπÑÏö∞ÏÑÝÌÉêÏÉâÏùÄ Í∑∏ÎûòÌîÑΕº ÌÉêÏÉâÌïòÍ∏∞ ÏúÑÌïú Í∞ÄÏû• Ïâ¨Ïö¥ ÏïåÍ≥Ýζ¨Ï¶ò ϧëÏóê ÌïòÎÇò ÏûÖÎãàÎã§.¬Ý ÌäπÏÝï ÏÝïÏÝê SΰúÎ∂ÄÌÑ∞ Ïó∞Í≤∞Îêú Ι®ÎìÝ ÏÝïÏÝêÎì§ÏùÑ Ï∞æÍ∏∞ ÏúÑÌï¥ Í∞ÑÏÑÝÎì§ÏùÑ ÌÉêÏÉâÌï©ÎãàÎã§.¬Ý Ïó¨Í∏∞ÏÑú Ï£ºÎ™©ÌïÝ ÏÝêÏùÄ SΰúÎ∂ÄÌÑ∞ ͱ∞ζ¨Í∞Ä K+1 Ïù∏ ÏÝïÏÝêÎì§ÏùÑ Ï∞æÍ∏∞ ÏÝÑÏóê Ι®ÎìÝ KÏù∏ Ι®ÎìÝ ÏÝïÏÝêÎì§ÏùÑ ÌÉêÏÉâÌïúÎã§Îäî Í≤É ÏûÖÎãàÎã§. ÏßÅÍ¥ÄÏÝÅÏù∏ Ïù¥Ìï¥Î•º ÎèïÍ∏∞ ÏúÑÌï¥ Ìä∏ζ¨Î°ú ÌëúÌòÑÌï¥Î≥¥ÎäîÍ≤å Í∞ÄÏû• Ï¢ãÏäµÎãàÎã§.¬Ý Ïù¥Ìï¥Î•º ÎèïÍ∏∞ ÏúÑÌï¥ ÏÝïÏÝêÎì§Ïùò ÏÉâÏÉÅÏùÄ Ìù∞ÏÉâÍ≥º ÌöåÏÉâ, Í∑∏ζ¨Í≥Ý Í≤ÄÏÝïÏÉâÏùÑ ÏǨÏö©Ìï¥ÏÑú¬ÝÎÑàÎπÑÏö∞ÏÑÝÌÉêÏÉâÏù¥ ÏßÑÌñâÎêòÎäî ÎèôÏïàÏùò Î≥ÄÌôîΕº ÌôïÏù∏ÌïÝ Ïàò ÏûàÏäµÎãàÎã§. ϵúÏ¥àÏóê Ι®ÎìÝ ÏÝïÏÝêÎì§ÏùÄ Ìù∞ÏÉâÏúºÎ°ú Ï¥àÍ∏∞Ìôî Îê©ÎãàÎã§. Í∑∏ζ¨Í≥Ý Î∞©Î¨∏ÌïòÍ≤å ÎêòÎäî ÏÝïÏÝêÏùÄ ÌöåÏÉâÏù¥ ÎêòÍ≥Ý, ÎçîÏù¥ÏÉÅ Ïù∏ÏÝëÌïú Ìù∞ÏÉâ ÏÝïÏÝêÏù¥ ÏóÜÏùÑÎïåÎäî Í≤ÄÏÝïÏÉâÏúºÎ°ú ÌëúÌòÑÌï©ÎãàÎã§.






![<?php
class Vertex
{
public function __construct($key)
{
$this->id = $key;
$this->connect_to = array();
}
public function addNeighbor($neighbor, $weight = 0)
{
$this->connect_to[$neighbor->getId()] = array('neighbor' => $neighbor, 'weight' =>
$weight);
}
public function getConnections()
{
return array_keys($this->connect_to);
}
public function getId()
{
return $this->id;
}
public function getWeight($neighbor)
{
return $this->connect_to[$neighbor->getId()]['weight'];
}
}
PHP ÌÅ¥ÎûòÏä§Î°ú ÏÝïÏÝêÏùò Ïù∏ÏÝë ζ¨Ïä§Ìä∏ ͵¨ÌòÑ
4 5
3
6](https://image.slidesharecdn.com/wptechtalkgraphwindows-151022045241-lva1-app6891/85/Graph-10-320.jpg)


![단어 사다리 그래프 구현<?php
require_once('Graph.php');
function buildGraph($word_file)
{
$container = array();
$graph = new Graph();
$f = fopen($word_file, "r");
if ($f) {
while (($word = fgets($f)) !== false) {
$container = setBucketContainer(trim($word));
}
fclose($f);
} else {
throw new Exception('파일을 읽을 수 없습니다.');
}
$bucket_keys = array_keys($container);
foreach ($bucket_keys as $bucket) {
foreach ($container[$bucket] as $word1) {
foreach ($container[$bucket] as $word2) {
if ($word1 != $word2) {
$graph->addEdge($word1, $word2);
}
}
}
}
return $graph;
}](https://image.slidesharecdn.com/wptechtalkgraphwindows-151022045241-lva1-app6891/85/Graph-14-320.jpg)
![단어 사다리 그래프 구현(2)
function setBucketContainer($word)
{
$container = array();
$word_length = strlen($word);
for ($i = 0; $i < $word_length; $i++) {
$bucket = substr($word, 0, $i) . '_' . substr($word, $i + 1, ($word_length - 1) - $i);
if (array_key_exists($bucket, $container)) {
array_push($container[$bucket], $word);
} else {
$container[$bucket] = array($word);
}
}
return $container;
}](https://image.slidesharecdn.com/wptechtalkgraphwindows-151022045241-lva1-app6891/85/Graph-15-320.jpg)

![ÎÑàÎπÑÏö∞ÏÑÝÌÉêÏÉâ(BFS) ͵¨ÌòÑfunction bfs($start_vertex)
{
$start_vertex->setDistance(0);
$start_vertex->setPredcessor(false);
$queue = array();
array_push($queue, $start_vertex);
while (count($queue) > 0) {
$current_vertext = array_shift($queue);
$neighbor = $current_vertext->getConnections();
foreach ($neighbor as $nbr_vertext) {
if ($nbr_vertext['neighbor']->getColor() == 'white') {
$nbr_vertext['neighbor']->setColor('gray');
$nbr_vertext['neighbor']->setDistance($current_vertext->getDistance() +
1);
$nbr_vertext['neighbor']->setPredecessor($current_vertext);
array_push($queue, $nbr_vertext['neighbor']);
}
}
$current_vertext->setColor('black');
}
}
bfs($word_radder->getVertex('fool'));](https://image.slidesharecdn.com/wptechtalkgraphwindows-151022045241-lva1-app6891/85/Graph-17-320.jpg)

