Graph Exploration Algorithm- Term Paper Presentation
- 1. Parallelizing Depth-First Search for Robotic Graph Exploration PRESENTED BY, VARUN NARANG B.TECH, MATHEMATICS AND COMPUTING IIT GUWAHATI
- 2. Background ’éŚ The collective behavior of robot swarms fits them for comprehensive search of an environment, which is useful for terrain mapping, crop pollination, and related applications. ’éŚ We study efficient mapping of an obstacle-ridden environment by a collection of robots.
- 3. Abstract ’éŚ We model the environment as an undirected, connected graph and require robots to explore the graph to visit all nodes and traverse all edges. ’éŚ Here we present a graph exploration algorithm that parallelizes depth-first search, so that each robot completes a roughly equal part of exploration.
- 4. Motivation ’éŚ We consider the task of exploring a field of crops that will subsequently be pollinated. ’éŚ Conducting exploration first is useful because once the robot swarm has mapped the field entirely, it can determine best paths to crops. ’éŚ The Harvard RoboBees project aims to build a colony of small, autonomously flying robotic bees that can accomplish pollination
- 5. Assumptions ’éŚ The environment is an undirected, connected graph whose nodes represent locations in the environment. ’éŚ Edges represent the ability to move directly from one location to another. ’éŚ An edge does not exist between adjacent locations if an obstacle separates them, and does exist otherwise. ’éŚ A colony of homogeneous robots resides at a hive, located at some node.
- 6. ’éŚ An unlimited number of robots may occupy a node simultaneously. ’éŚ At each time step, each robot starts at a node and traverses an edge as instructed by the hive. ’éŚ We have implicitly assumed robots have perfect odometry-they know their exact change in position at every step. This implies robots always know their coordinates relative to the hive. ’éŚ Exploration should terminate when the hive knows all nodes and all edges. To this end, at each step all robots transmit their locations back to the hive and notify the hive of any crops detected.
- 7. Formal Model ’éŚ The environment is an undirected graph G=(V;E). ’éŚ An edge {v1, v2} ╬Ą E if no obstacle separates v1 and v2. ’éŚ We require that G is connected so that all nodes are reachable from vh. ’éŚ Based on the edges robots traverse and the nodes where robots end up, the hive gradually builds a map of G, denoted Gm = (Vm, Em). Every node visited for the first time is added to Vm; every edge traversed for the first time is added to Em.
- 8. Some Key Terms ’éŚ Nodes are labeled if each node contains information that uniquely identifies it, and unlabeled otherwise. ’éŚ A graph has labeled nodes if a robot can recognize a node it has visited previously. ’éŚ Undirected edges: The robot can move in either direction on the edge then it is an undirected edge.
- 9. DFS algorithm ’éŚ Depth-first search, or DFS, is a way to traverse the graph. ’éŚ Initially it allows visiting vertices of the graph only, but there are hundreds of algorithms for graphs, which are based on DFS. ’éŚ The principle of the algorithm is quite simple: to go forward (in depth) while there is such possibility, otherwise to backtrack.
- 11. Complexity analysis ’éŚ Assume that graph is connected. ’éŚ Depth-first search visits every vertex in the graph and checks every edge its edge. Therefore, DFS complexity is O(V + E). ’éŚ If an adjacency matrix is used for a graph representation, then all edges, adjacent to a vertex can't be found efficiently, that results in O(V2) complexity. ’éŚ DFS algorithm traverses undirected graphs with labeled nodes, making 2*|E| edge traversals. Two along every edge.
- 12. ’éŚ Since any graph traversal requires at least |E| edge traversals, and DFS requires 2|E| edge traversals, the overhead of DFS is 2. ’éŚ For general graphs, even if the robot is given an unlabeled map, an overhead of 2 is optimal; thus DFS is a generally optimal algorithm with respect to the authors' metric.
- 13. How to Reduce Overhead? ’éŚ Multiple robots should be able to divide the work of exploration and reduce runtime more dramatically. ’éŚ Thus, our approach is to parallelize DFS.
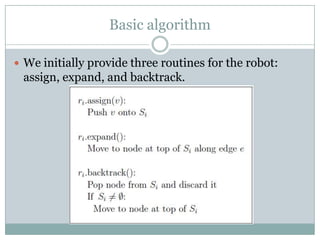
- 14. Basic algorithm ’éŚ We initially provide three routines for the robot: assign, expand, and backtrack.
- 15. DFS Algorithm ’éŚ Initially all vertices are white (unvisited). ’éŚ DFS starts in arbitrary vertex and runs as follows: ’éĪ Mark vertex u as gray (visited). ’éĪ For each edge (u, v), where u is white, run depth-first search for u recursively. ’éĪ Mark vertex u as black and backtrack to the parent.
- 16. Each iteration of the while loop represents one time step. ’āś At each time step, each robot traverses at most one edge. ’āś A robot at a finished node cannot expand, so it backtracks. ’āś A robot at a started but unfinished node should expand an edge. ’āś A robot at an un started node should expand an edge if one exists; otherwise it should backtrack because the node is already finished (the robot has reached a dead end).
- 17. ’éŚ The hive waits until the end of the iteration to direct expanding robots where to go. ’éŚ It groups robots based on their current node, then, for each node with a robot, the unexplored edges are divided evenly among all the robots there. ’éŚ Robots expand their assigned edges, and the hive adds these newly explored edges to Em.
- 18. Correctness Claim 1. PDFS terminates when G is completely explored. ’éŚ Proof. Suppose G is completely explored. All nodes have been finished, so the robots backtrack until their stacks are empty. This is the termination condition of PDFS. ’éŚ Now suppose PDFS terminates at time T. ’éŚ All nodes have been finished by time T.
- 19. Efficiency Analysis ’éŚ The runtime is the number of times the outer while loop of PDFS iterates. We investigate the worst case run time of the algorithm. ’éŚ For every k Ōēź 1, ╬Ą< 1, we can construct a graph such that PDFS has runtime at least 2|E|(1- ╬Ą ).
- 20. Proof (Efficiency) ’éŚ Consider the graph in Figure 3.1, consisting of a ŌĆ£stem" of length r and a ŌĆ£trap" with B edges, where B is high. ’éŚ The hive is the leftmost node of degree 3. The idea is to use up all robots except one to explore the stem, and leave the remaining robot to explore the trap.
- 21. ’éŚ We have two cases: ’éŚ Case 1: k=3m ’éĪ At the i th iteration , 3m-i robots make it i-nodes down the stem, where there is unfinished work. ’éĪ In the first iteration, PDFS assigns 3(m-1) robots to each of the branches above and below the hive. These robots arrive at finished nodes, backtrack to the hive and do nothing. ’éĪ At iteration m, a single robot makes it m nodes down the stem and enters the trap. ’éĪ All other robots fall into two categories: those with empty stacks, which are doing nothing, and those whose stacks contain only finished nodes, which are backtracking to the hive. ’éĪ This graph contains three edges per unit length of the stem, so |E| = 3r +B. ’éĪ The runtime is the time taken by the robot that enters the trap: 2r to travel across the stem and back, and 2B to explore the trap by single-robot DFS. We want 2r + 2B Ōēż 2|E|(1-╬Ą) for our claim to hold.
- 22. We simply construct a graph with r = m and appropriate B. Case 2.k is not a power of 3. We choose r = Ōöī log3 (k), ŌöÉmaking the stem long enough to ensure only one robot enters the trap. We choose B according to the equations above are satisfied.
- 23. Worst-Case Runtime ’éŚ The worst-case runtime of PDFS is 2|E|
- 24. Remarks ’éŚ PDFS performs no better than single-robot DFS in the worst case. ’éŚ PDFS cannot take advantage of multiple robots when, in a perverse graph, many robots finish their work, and some robot becomes the bottleneck. ’éŚ We cannot allocate nished robots to unfinished work because our requirement that there be no wasteful edge traversals prevents them from leaving the hive after finishing DFS.
- 25. Acknowledgements ’éŚ Parallelizing Depth-First Search for Robotic Graph Exploration by Chelsea Zhang, Harvard College, Cambridge, Massachusetts--April 1, 2010 ’éŚ Distributed Graph Exploration- Gerard Tel-- April 1997 ’éŚ Wikipedia ’üŖ