Halftone structure optimization using convex programming
- 1. METRIC BASED HALFTONE PATTERN OPTIMIZATION USING CONVEX PROGRAMMING PETER MOROVI─ī, J├üN MOROVI─ī, VICTOR DIEGO, JAVIER MAESTRO, XAVI FARI├æA, PERE GASPARIN HP INC., BARCELONA, CATALONIA, SPAIN
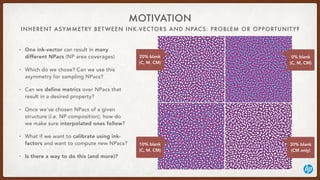
- 2. INHERENT ASYMMETRY BETWEEN INK-VECTORS AND NPACS: PROBLEM OR OPPORTUNITY? MOTIVATION ŌĆó One ink-vector can result in many different NPacs (NP area coverages) ŌĆó Which do we chose? Can we use this asymmetry for sampling NPacs? ŌĆó Can we define metrics over NPacs that result in a desired property? ŌĆó Once weŌĆÖve chosen NPacs of a given structure (i.e. NP composition), how do we make sure interpolated ones follow? ŌĆó What if we want to calibrate using ink- factors and want to compute new NPacs? ŌĆó Is there a way to do this (and more)? 0% blank (C, M, CM) 30% blank (CM only) 20% blankŌĆ© (C, M, CM) 10% blankŌĆ© (C, M, CM)
- 3. DECIDING HALFTONE STATISTICS BEFORE HALFTONING HANS PIPELINE CHOICES Contone InputŌĆ© (RGB) NPacs HalftoneŌĆ© (NPs) Tetrahedral interpolation PARAWACS Contone InputŌĆ© (RGB) Ink-vectors HalftoneŌĆ© (NPs) Tetrahedral interpolation Error Diffusion or Matrix HALFTONE CONTENTS HALFTONE CONTENTS & SPATIAL DISTRIBUTION SPATIAL DISTRIBUTION
- 4. CONSTRAINED MAPPING OF INK-VECTORS TO NPACS CONVEX OPTIMIZATION Y:0.143, YY:0.143, KY:0.143, kY:0.143, kK:0.143, K:0.143, k:0.143 Input NPac kK:0.43, kY:0.57 Output NPacŌĆÖMetric Constraints Convex Optimization Ink-vector change Min || H(NPac) + f(NPac) || Sum(NPac) == 1, 0 <= NPac <= 1 All NPs from Global_NP Set InkVec(NPacŌĆÖ) == InkVec(NPac)*factors ŌĆó HANS pipeline controls pixel types (NPs) ŌåÉ HP Pixel Control ŌĆó Given an ink-vector (or an NPac), LP allows us to penalize/reward NP types (QP can take it further) ŌĆó Every NPac can be optimized, given such metric, resulting in consistent NPacs
- 5. SIMPLE EXAMPLE CONVEX OPTIMIZATION INK-VECTOR: 50% CYAN INK 50% MAGENTA INK NPS: [BLANK, C, M, CM] OBJECTIVE FUNCTION F1 = [100, 0, 0, 0] OBJECTIVE FUNCTION F2 = [0, 100, 100, 0] NPac: 50% C 50% M NPac: 50% CM 50% Blank
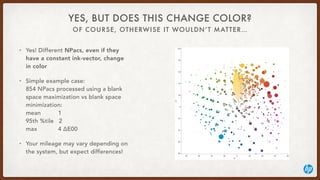
- 6. OF COURSE, OTHERWISE IT WOULDNŌĆÖT MATTERŌĆ” YES, BUT DOES THIS CHANGE COLOR? -80 -60 -40 -20 0 20 40 60 80 a* -80 -60 -40 -20 0 20 40 60 80 100 b* Default vs W-MAX ŌĆó Yes! Different NPacs, even if they have a constant ink-vector, change in color ŌĆó Simple example case:ŌĆ© 854 NPacs processed using a blank space maximization vs blank space minimization:ŌĆ© mean ┬Ā 1ŌĆ© 95th %tile ┬Ā 2 ŌĆ© max ┬Ā 4 ╬öE00 ŌĆó Your mileage may vary depending on the system, but expect differences!
- 7. MINIMIZE NP CONTRAST FOR ALL NPACS OF A LUT ŌĆō┬ĀIMPACT ON GRAIN EXAMPLE: IQ OPTIMIZATION LUT USING 200 NPS VIA OPTIMISATIONŌĆ© FAVOURING OVERPRINTING AND PENALISING BLANK SPACE LUT USING 31 NPS VIA AN NP REDUCTIONŌĆ© AND SIDE-BY-SIDE OPTIMIZATION HIGH SPEED HIGH QUALITY
- 8. REPURPOSE IMPORTED INK-VECTOR LUT TO IMPROVE IQ EXAMPLE: LUT IMPORTING Native (TDFED, ink-channels) HANS (PARAWACS, NPacs) ~.5 cm SMOOTHNESS COMPARISON (APPROXIMATELY AT 100% ZOOM) GRAIN COMPARISONŌĆ© (CROP APPROX.ŌĆ© 0.5 CM WIDTH)
- 9. SAME INK-VECTOR, DIFFERENT NPACS, DIFFERENT GRAIN EXAMPLE: GRAIN SAMPLES MINIMIZING OVERPRINTING (SINGLE-INK NPS OR LOW DROP STATES MOST COMMON) GIVEN AN INK-VECTOR, COMPUTE DIFFERENT ALTERNATIVE NPACS THAT VARY IN GRAIN (MORE OR LESS OVERPRINTING, MORE OR LESS BLANK SPACE, ETC.). MAXIMIZING OVERPRINTING (MULTI-INK NPS OR HIGHER DROP STATES MOST COMMON)
- 10. FROM MEASURED INK-VECTOR RATIOS TO IQ-MAINTAINING CHANGED NPACS EXAMPLE: CALIBRATION -80 -60 -40 -20 0 20 40 60 a* -60 -40 -20 0 20 40 60 80 100b* Color difference (vs reference printer) before calibration -80 -60 -40 -20 0 20 40 60 a* -60 -40 -20 0 20 40 60 80 100 b* Color difference (vs reference printer) after calibration CALIBRATED MED: 0.7 95%: 1.4 MAX: 1.9 UNCALIBRATED MED: 1.2 95%: 2.7 MAX: 3.5
- 11. CONCLUSIONS ŌĆó Convex optimization provides a powerful and flexible framework for algorithmically dealing with the relationship of ink-vectors and NPacs ŌĆó It allows us to introduce NPac structure that directly affects print attributes ŌĆó We successfully applied this approach to: ink-vector sampling, LUT node optimization, local grain sampling, ink-factor based color calibration HP Pixel Control HP Pixel Control HP Pixel Control Photos ┬® Lee Jeffries
- 12. THANK YOU!




![SIMPLE EXAMPLE
CONVEX OPTIMIZATION
INK-VECTOR:
50% CYAN INK
50% MAGENTA INK
NPS:
[BLANK, C, M, CM]
OBJECTIVE FUNCTION
F1 = [100, 0, 0, 0]
OBJECTIVE FUNCTION
F2 = [0, 100, 100, 0]
NPac:
50% C
50% M
NPac:
50% CM
50% Blank](https://image.slidesharecdn.com/cic26npacoptimizationkey-181126092029/85/Halftone-structure-optimization-using-convex-programming-5-320.jpg)