H√†m sŠĽĎ - 3. ńźŠĽď thŠĽč h√†m sŠĽĎ
- 1. 3 ńźŠĽí THŠĽä H√ÄM SŠĽź - NH√ďM 1 3.1 L√Ě THUYŠļĺT 3.1.1 C√°c b∆įŠĽõc khŠļ£o s√°t sŠĽĪ biŠļŅn thi√™n v√† vŠļĹ ńĎŠĽď thŠĽč h√†m sŠĽĎ B∆įŠĽõc 1 T√¨m tŠļ≠p x√°c ńĎŠĽčnh cŠĽßa h√†m sŠĽĎ B∆įŠĽõc 2: X√©t sŠĽĪ biŠļŅn th√™n cŠĽßa h√†m sŠĽĎ - T√¨m giŠĽõi hŠļ°n tŠļ°i v√ī cŠĽĪc v√† giŠĽõi hŠļ°n v√ī cŠĽĪc (nŠļŅu c√≥) cŠĽßa h√†m sŠĽĎ, c√°c ńĎ∆įŠĽĚng tiŠĽám cŠļ≠n cŠĽßa ńĎŠĽď thŠĽč (nŠļŅu c√≥) - LŠļ≠p bŠļ£ng biŠļŅn th√™n cŠĽßa h√†m sŠĽĎ: T√¨m ńĎŠļ°o h√†m, x√©t dŠļ•u ńĎŠļ°o h√†m, x√©t chiŠĽĀu biŠļŅn thi√™n, t√¨m cŠĽĪc trŠĽč cŠĽßa h√†m sŠĽĎ (nŠļŅu c√≥) B∆įŠĽõc 3: VŠļĹ ńĎŠĽď thŠĽč h√†m sŠĽĎ - VŠļĹ c√°c ńĎ∆įŠĽĚng tiŠĽám cŠļ≠n cŠĽßa ńĎŠĽď thŠĽč (nŠļŅu c√≥) - X√°c ńĎŠĽčnh mŠĽôt sŠĽĎ ńĎiŠĽÉm ńĎŠļ∑c biŠĽát cŠĽßa ńĎŠĽď thŠĽč - NhŠļ≠n x√©t: TrŠĽ•c, t√Ęm ńĎŠĽĎi xŠĽ©ng cŠĽßa ńĎŠĽď thŠĽč. 3.1.2 MŠĽôt sŠĽĎ dŠļ°ng ńĎŠĽď thŠĽč th∆įŠĽĚng gŠļ∑p * H√†m sŠĽĎ y = ax3 + bx2 + cx + d x y 0 x y 0 y = 1 8 (x3 ‚ąí 3x2 ‚ąí 9x ‚ąí 5) y = ‚ąíx3 + 3x2 ‚ąí 4x + 2 Ch√ļ √Ĺ: ńźŠĽď thŠĽč cŠĽßa h√†m sŠĽĎ bŠļ≠c ba f(x) = ax3 + bx2 + cx + d lu√īn c√≥ mŠĽôt ńĎiŠĽÉm uŠĽĎn v√† ńĎiŠĽÉm ńĎ√≥ l√† t√Ęm ńĎŠĽĎi xŠĽ©ng cŠĽßa ńĎŠĽď thŠĽč h√†m sŠĽĎ d√£ cho * H√†m tr√Ļng ph∆į∆°ng y = ax4 + bx2 + c(a = 0) x y 0 -1 -2 x y 0-1 1 y = x4 ‚ąí 2x2 ‚ąí 1 y = ‚ąíx4 ‚ąí 2x2 + 3 15 lovestem .edu.vn
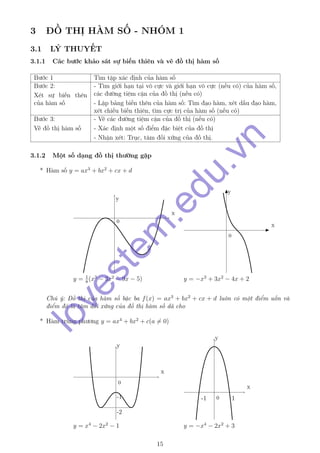
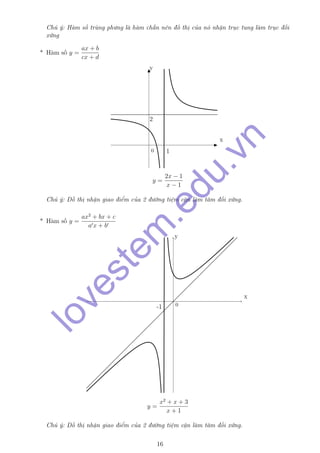
- 2. Ch√ļ √Ĺ: H√†m sŠĽĎ tr√Ļng ph∆įng l√† h√†m chŠļĶn n√™n ńĎŠĽď thŠĽč cŠĽßa n√≥ nhŠļ≠n trŠĽ•c tung l√†m trŠĽ•c ńĎŠĽĎi xŠĽ©ng * H√†m sŠĽĎ y = ax + b cx + d x y 0 1 2 y = 2x ‚ąí 1 x ‚ąí 1 Ch√ļ √Ĺ: ńźŠĽď thŠĽč nhŠļ≠n giao ńĎiŠĽÉm cŠĽßa 2 ńĎ∆įŠĽĚng tiŠĽám cŠļ≠n l√†m t√Ęm ńĎŠĽĎi xŠĽ©ng. * H√†m sŠĽĎ y = ax2 + bx + c a x + b x y 0-1 y = x2 + x + 3 x + 1 Ch√ļ √Ĺ: ńźŠĽď thŠĽč nhŠļ≠n giao ńĎiŠĽÉm cŠĽßa 2 ńĎ∆įŠĽĚng tiŠĽám cŠļ≠n l√†m t√Ęm ńĎŠĽĎi xŠĽ©ng. 16 lovestem .edu.vn
- 3. 3.1.3 V√≠ dŠĽ• minh hŠĽća C√Ęu 1. H√¨nh b√™n l√† ńĎŠĽď thŠĽč h√†m sŠĽĎ n√†o trong c√°c h√†m sŠĽĎ sau x y O-1 2 A. y = x2 (x + 1)(x ‚ąí 2). B. y = ‚ąíx3 + x2 + 2x. C. y = x3 ‚ąí x2 ‚ąí 2x. D. y = x4 ‚ąí x2 . LŠĽĚi giŠļ£i. ChŠĽćn ńĎ√°p √°n C ńźŠĽď thŠĽč ńĎ√£ cho l√† ńĎŠĽď thŠĽč h√†m sŠĽĎ bŠļ≠c ba y = ax3 + bx2 + cx + d. Cho x ‚Üí ‚ąí‚ąě th√¨ y ‚Üí ‚ąí‚ąě n√™n a > 0. C√Ęu 2. Cho ńĎŠĽď thŠĽč h√†m sŠĽĎ y = f(x) nh∆į h√¨nh vŠļĹ b√™n. T√¨m m ńĎŠĽÉ ph∆į∆°ng tr√¨nh f(x) = m c√≥ 2 nghiŠĽám ph√Ęn biŠĽát x y -1 O A. y = x2 (x + 1)(x ‚ąí 2). B. y = ‚ąíx3 + x2 + 2x. C. y = x3 ‚ąí x2 ‚ąí 2x. D. y = x4 ‚ąí x2 . LŠĽĚi giŠļ£i. ChŠĽćn ńĎ√°p √°n C SŠĽĎ nghiŠĽám cŠĽßa ph∆į∆°ng tr√¨nh f(x) = m l√† sŠĽĎ giao ńĎiŠĽÉm cŠĽßa ńĎ∆įŠĽĚng thŠļ≥ng y = m vŠĽõi ńĎŠĽď thŠĽč h√†m sŠĽĎ f(x). Suy ra m ‚ąą {‚ąí1} ‚ą™ (0; +‚ąě) 3.2 B√ÄI TŠļ¨P 3.2.1 C√āU HŠĽéI ŠĽě MŠĽ®C ńźŠĽė NHŠļ¨N BIŠļĺT C√Ęu 3. ńź∆įŠĽĚng cong cŠĽßa h√¨nh vŠļĹ b√™n l√† ńĎŠĽď thŠĽč cŠĽßa h√†m sŠĽĎ n√†o trong c√°c h√†m sŠĽĎ sau: 17 lovestem .edu.vn
- 4. ‚ąí2 ‚ąí1 1 2 x y ‚ąí2 ‚ąí1 1 2 O A. y = ‚ąíx3 . B. y = x3 . C. y = x4 . D. y = ‚ąíx2 . C√Ęu 4. ńź∆įŠĽĚng cong nh∆į h√¨nh vŠļĹ b√™n l√† ńĎŠĽď thŠĽč cŠĽßa h√†m sŠĽĎ n√†o d∆įŠĽõi ńĎ√Ęy ‚ąí1 1 2 3 4 x y ‚ąí3 ‚ąí2 ‚ąí1 1 2 3 O A. y = x(x ‚ąí 3)2 . B. y = x4 ‚ąí 9x2 . C. y = x(x ‚ąí 3) x ‚ąí 1 . D. y = ‚ąíx(x ‚ąí 3)2 . C√Ęu 5. ńźŠĽď thŠĽč ŠĽü h√¨nh b√™n l√† cŠĽßa ńĎŠĽď thŠĽč h√†m sŠĽĎ n√†o sau ńĎ√Ęy x y -1 1 2 O 18 lovestem .edu.vn
- 5. A. 2x + 1 x ‚ąí 1 . B. ‚ąí2x + 1 x ‚ąí 1 . C. 2x + 1 x . D. 2x ‚ąí 2 x . C√Ęu 6. ńźŠĽď thŠĽč nh∆į h√¨nh vŠļĹ b√™n l√† ńĎŠĽď thŠĽč cŠĽßa h√†m sŠĽĎ x y -1 O A. y = x4 + 2x2 . B. y = x4 ‚ąí 2x2 . C. y = x3 ‚ąí 2x2 . D. y = x3 ‚ąí 2x. 3.2.2 C√āU HŠĽéI ŠĽě MŠĽ®C ńźŠĽė TH√ĒNG HIŠĽāU C√Ęu 7. H√¨nh vŠļĹ b√™n l√† ńĎŠĽď thŠĽč cŠĽßa h√†m sŠĽĎ y = ax3 +bx+c. TŠĽēng a+b+c bŠļĪng gi√° trŠĽč n√†o sau ńĎ√Ęy x y -2 2 -1 1 A. 0. B. ‚ąí2. C. 1. D. ‚ąí1. C√Ęu 8. ńź∆įŠĽĚng cong trong h√¨nh d∆įŠĽõi ńĎ√Ęy ‚ąí1 1 ‚ąí2 1 x y 0 l√† ńĎŠĽď thŠĽč h√†m sŠĽĎ n√†o trong c√°c h√†m sau: A. y = x4 ‚ąí 2x2 + 1. B. y = ‚ąíx4 ‚ąí 2x2 + 1 . C. y = ‚ąíx4 + 2x2 + 1. D. y = x4 + 2x2 + 1. 19 lovestem .edu.vn
- 6. C√Ęu 9. Gi√° trŠĽč a, b, c ńĎŠĽÉ h√†m sŠĽĎ y = ax3 + bx2 + c c√≥ ńĎŠĽď thŠĽč nh∆į h√¨nh vŠļĹ b√™n l√† x y O-1 -2 2 2 A. a = ‚ąí1, b = ‚ąí3, c = 2. B. a = ‚ąí1, b = 3, c = 2. C. a = 1, b = ‚ąí3, c = 2. D. a = 1, b = ‚ąí3, c = 2. C√Ęu 10. Cho ńĎŠĽď thŠĽč h√†m sŠĽĎ y = f(x) nh∆į h√¨nh vŠļĹ b√™n. ńźŠĽď thŠĽč trong ńĎ√°p √°n n√†o sau ńĎ√Ęy l√† ńĎŠĽď thŠĽč cŠĽßa h√†m sŠĽĎ y = f(|x|) x y -1 1 2 O A. x y -1 1 2 O . B. x y -1 1 2 O . 20 lovestem .edu.vn
- 7. C. x y -1 1 2 O . D. x y -1 1 2 O . C√Ęu 11. Cho ńĎŠĽď thŠĽč h√†m sŠĽĎ y = f(x) nh∆į h√¨nh vŠļĹ b√™n. ńźŠĽď thŠĽč trong ńĎ√°p √°n n√†o sau ńĎ√Ęy l√† ńĎŠĽď thŠĽč cŠĽßa h√†m sŠĽĎ y = |f(x)| x y -1 1 2 O A. x y -1 1 2 O . B. x y -1 1 2 O . 21 lovestem .edu.vn
- 8. C. x y -1 1 2 O . D. x y -1 1 2 O . C√Ęu 12. Cho ńĎŠĽď thŠĽč h√†m sŠĽĎ y = (x ‚ąí 2)(x + 1)2 nh∆į h√¨nh b√™n. ńźŠĽď thŠĽč trong ph∆į∆°ng √°n n√†o sau ńĎ√Ęy l√† ńĎŠĽď thŠĽč h√†m sŠĽĎ y = |x ‚ąí 2|(x + 1)2 : x y O 2 -4 A. x y O 2 4 . B. x y O 2 4 . C. x y O 2 4 . D. x y 2 4 . C√Ęu 13. Cho ńĎŠĽď thŠĽč h√†m sŠĽĎ y = f(x) nh∆į h√¨nh b√™n. ńźŠĽď thŠĽč n√†o trong c√°c ph∆į∆°ng √°n d∆įŠĽõi ńĎ√Ęy l√† ńĎŠĽď thŠĽč h√†m sŠĽĎ y = ‚ąíf(x) 22 lovestem .edu.vn
- 9. x y O 2 -2 2 A. x y O 2 2 . B. x y O 2 2 . C. x y O 2 -2 -2 2 . D. x y O 2 -2 2 . C√Ęu 14. Cho ńĎŠĽď thŠĽč h√†m sŠĽĎ y = f(x) nh∆į h√¨nh b√™n. ńźŠĽď thŠĽč n√†o trong c√°c ph∆į∆°ng √°n d∆įŠĽõi ńĎ√Ęy l√† ńĎŠĽď thŠĽč h√†m sŠĽĎ y = |f(x)| 23 lovestem .edu.vn
- 10. x y O 2 -2 2 A. x y O 2 2 . B. x y O 2 2 . C. x y O 2 -2 -2 2 . D. x y O 2 2 -2 . C√Ęu 15. Cho ńĎŠĽď thŠĽč h√†m sŠĽĎ y = f(x) nh∆į h√¨nh vŠļĹ b√™n. T√¨m m ńĎŠĽÉ ph∆į∆°ng tr√¨nh f(x) = m c√≥ nghiŠĽám x y O -1 A. m ‚ąą (0; +‚ąě). B. m ‚ąą [0; +‚ąě) . C. m ‚ąą {‚ąí1} ‚ą™ (0; +‚ąě). D. m ‚ąą [‚ąí1; +‚ąě). 24 lovestem .edu.vn
- 11. 3.2.3 C√āU HŠĽéI ŠĽě MŠĽ®C ńźŠĽė VŠļ¨N DŠĽ§NG C√Ęu 16. Cho ńĎŠĽď thŠĽč h√†m sŠĽĎ y = f(x) nh∆į h√¨nh vŠļĹ. Gi√° trŠĽč m ńĎŠĽÉ ńĎ∆į∆°ng thŠļ≥ng y = m cŠļĮt ńĎŠĽď thŠĽč h√†m sŠĽĎ y = f(|x|) tŠļ°i 2 ńĎiŠĽÉm ph√Ęn biŠĽát l√† x y O 2 -2 2 A. m = ‚ąí2, m > 2.. B. m = ‚ąí2, m = 2.. C. m > 2.. D. m ‚ȧ ‚ąí2.. C√Ęu 17. Cho ńĎŠĽď thŠĽč h√†m sŠĽĎ y = f(x) nh∆į h√¨nh b√™n. T√¨m m ńĎŠĽÉ ph∆į∆°ng tr√¨nh f(x) = m2 ‚ąí 2m c√≥ 2 nghiŠĽám ph√Ęn biŠĽát x y O 2 -4 A. m ‚ȧ 0. B. m ‚Č• 0. C. m ‚ąą {‚ąí2, 0}. D. m ‚ąą {‚ąí2, 0, 2}. C√Ęu 18. Cho ńĎŠĽď thŠĽč h√†m sŠĽĎ y = f(x) nh∆į h√¨nh b√™n. ńźŠĽď thŠĽč n√†o trong c√°c ph∆į∆°ng √°n d∆įŠĽõi ńĎ√Ęy l√† ńĎŠĽď thŠĽč h√†m sŠĽĎ y = |f(|x|)| x y O 2 -2 2 25 lovestem .edu.vn
- 12. A. x y O 2 2 -2 . B. x y O 2 2 . C. x y O 2 -2 -2 2 . D. x y O 2 2 . C√Ęu 19. Cho ńĎŠĽď thŠĽč h√†m sŠĽĎ y = f(x) nh∆į h√¨nh vŠļĹ b√™n. ńźŠĽď thŠĽč trong ńĎ√°p √°n n√†o sau ńĎ√Ęy l√† ńĎŠĽď thŠĽč cŠĽßa h√†m sŠĽĎ y = |f(|x|)| x y -1 1 2 O 26 lovestem .edu.vn
- 13. A. x y -1 1 2 O . B. x y -1 1 2 O . C. x y -1 1 2 O . D. x y -1 1 2 O . LŠĽĚi giŠļ£i. ChŠĽćn ńĎ√°p √°n C X√©t ńĎŠĽď thŠĽč h√†m sŠĽĎ y = |f(x)| rŠĽďi x√©t ńĎŠĽď thŠĽč h√†m sŠĽĎ y = |f(|x|)| ńźŠĽď thŠĽč h√†m sŠĽĎ y = |f(x)| x y -1 1 2 O Suy ra ńĎŠĽď thŠĽč h√†m sŠĽĎ y = |f(|x|)| x y -1 1 2 O C√Ęu 20. Cho ńĎŠĽď thŠĽč f(x) nh∆į h√¨nh vŠļĹ b√™n. Gi√° trŠĽč cŠĽßa m ńĎŠĽÉ ńĎ∆įŠĽĚng thŠļ≥ng y = m cŠļĮt ńĎŠĽď thŠĽč h√†m sŠĽĎ y = |f(x)| tŠļ°i 6 ńĎiŠĽÉm ph√Ęn biŠĽát l√†: 27 lovestem .edu.vn
- 14. x y O -1 A. 0 < m < 1. B. m = 1 . C. m = 0. D. m ‚ȧ 0. C√Ęu 21. Gi√° trŠĽč cŠĽßa a, b ńĎŠĽÉ h√†m sŠĽĎ y = ax + b x ‚ąí 1 c√≥ ńĎŠĽď thŠĽč nh∆į h√¨nh vŠļĹ l√†: x y -2 -2 1 1O A. a = ‚ąí1, b = 2. B. a = 1, b = ‚ąí2. C. a = ‚ąí1, b = ‚ąí2. D. a = 1, b = 2. 3.2.4 C√āU HŠĽéI ŠĽě MŠĽ®C ńźŠĽė N√āNG CAO C√Ęu 22. ńźŠĽÉ ńĎŠĽď thŠĽč h√†m sŠĽĎ y = ax3 + bx2 + cx + d c√≥ dŠļ°ng nh∆į h√¨nh vŠļĹ b√™n th√¨ ńĎiŠĽĀu kiŠĽán cŠĽßa a, b, c l√† x y O 28 lovestem .edu.vn
- 15. A. a > 0 b2 ‚ąí 3ac > 0 . B. a < 0 b2 ‚ąí 3ac > 0 . C. a > 0 b2 ‚ąí 3ac < 0 . D. a < 0 b2 ‚ąí 3ac < 0 . LŠĽĚi giŠļ£i. ChŠĽćn ńĎ√°p √°n B Cho x ‚Üí ‚ąí‚ąě th√¨ y ‚Üí +‚ąě n√™n a < 0 y = 3ax2 + 2bx + c, h√†m sŠĽĎ c√≥ 2 ńĎiŠĽÉm cŠĽĪc trŠĽč n√™n ph∆į∆°ng tr√¨nh y = 0 c√≥ 2 nghiŠĽám ph√Ęn biŠĽát, hay b2 ‚ąí 3ac > 0. C√Ęu 23. Cho ńĎŠĽď thŠĽč h√†m sŠĽĎ y = f(x) nh∆į h√¨nh vŠļĹ b√™n. G√≠a trŠĽč m ńĎŠĽÉ ńĎ∆į∆°ng thŠļ≥ng y = m cŠļĮt ńĎŠĽď thhij h√†m sŠĽĎ y = |f(|x|)| tŠļ°i 4 ńĎiŠĽÉm ph√Ęn biŠĽát l√† x y 2 -2 O A. ‚ąí2 < m < 2.. B. m = 2.. C. m = 0.. D. m = 2, m = 0.. LŠĽĚi giŠļ£i. ChŠĽćn ńĎ√°p √°n C ńźŠĽď thŠĽč cŠĽßa h√†m sŠĽĎ y = |f(|x|)| nh∆į h√¨nh vŠļĹ x y 2 -1 1 ńź∆įŠĽĚng thŠļ≥ng y = m cŠļĮt ńĎŠĽď thŠĽč h√†m sŠĽĎ y = |f(|x|)| tŠļ°i 4 ńĎiŠĽÉm ph√Ęn biŠĽát khi m = 0. C√Ęu 24. Cho ńĎŠĽď thŠĽč h√†m sŠĽĎ y = (x2 ‚ąí 1)(x ‚ąí 3) nh∆į h√¨nh b√™n. ńźŠĽď thŠĽč trong ph∆į∆°ng √°n n√†o sau ńĎ√Ęy l√† ńĎŠĽď thŠĽč h√†m sŠĽĎ y = |x2 ‚ąí 1|(x ‚ąí 3) 29 lovestem .edu.vn
- 16. x y 3-1 1 A. x y 3-1 1 . B. x y 3-1 1 . C. x y 3-1 1 . D. x y 3-1 1 . LŠĽĚi giŠļ£i. ChŠĽćn ńĎ√°p √°n D Ta c√≥ y = |x2 ‚ąí 1|(x ‚ąí 3) = (x2 ‚ąí 1)(x ‚ąí 3) khi x2 ‚ąí 1 ‚ȧ 0 ‚ąí(x2 ‚ąí 1)(x ‚ąí 3) khi x2 ‚ąí 1 < 0 N√™n ńĎŠĽď thŠĽč h√†m sŠĽĎ y = |x2 ‚ąí 1|(x ‚ąí 3) gŠĽďm 2 phŠļßn: 30 lovestem .edu.vn
- 17. PhŠļßn 1: PhŠļßn ńĎŠĽď thŠĽč h√†m sŠĽĎ (x2 ‚ąí 1)(x ‚ąí 3) khi x ‚ąą (‚ąí‚ąě; ‚ąí1] ‚ą™ [1; +‚ąě) PhŠļßn 2: PhŠļßn ńĎŠĽĎi xŠĽ©ng vŠĽõi ńĎŠĽď thŠĽč h√†m sŠĽĎ (x2 ‚ąí 1)(x ‚ąí 3) khi x ‚ąą (‚ąí1; 1) 31 lovestem .edu.vn














![PhŠļßn 1: PhŠļßn ńĎŠĽď thŠĽč h√†m sŠĽĎ (x2
‚ąí 1)(x ‚ąí 3) khi x ‚ąą (‚ąí‚ąě; ‚ąí1] ‚ą™ [1; +‚ąě)
PhŠļßn 2: PhŠļßn ńĎŠĽĎi xŠĽ©ng vŠĽõi ńĎŠĽď thŠĽč h√†m sŠĽĎ (x2
‚ąí 1)(x ‚ąí 3) khi x ‚ąą (‚ąí1; 1)
31
lovestem
.edu.vn](https://image.slidesharecdn.com/hamso-wm-pages-15-31-181101115256/85/Ham-s-3-D-th-ham-s-17-320.jpg)