![solution
1. The Evaluation Problem - Forward
HMM parameter μ=(π,A,B)
forward probability : αj(t) when time = t，observation sequence
(o1,o2,…,ot)，the probability of hidden state j
when t = 1
[ ]](https://image.slidesharecdn.com/hmm-170325023436/85/Hidden-markov-model-8-320.jpg)
![S1
S2 S3
S1-diff(μ, σ2)
S1-volume(μ, σ2)
S2-diff(μ, σ2)
S2-volume(μ, σ2)
S3-diff(μ, σ2)
S3-volume(μ, σ2)
S = 3
O = 2
Gaussian = 3*2 = 6
如果每?一個S所噴出O的結果符合 gaussian normal distribution
diff = close_v(today) - close_v(yesterday)
volume = volume(today)
O =[diff, volume]
S1 : rise
S2：decline
S3：calm](https://image.slidesharecdn.com/hmm-170325023436/85/Hidden-markov-model-24-320.jpg)
![S
O
Discrete
Continuous
Gaussian HMM of stock data
diff = close_v(today) - close_v(yesterday)
volume = volume(today)
O =[diff, volume]
S1 S2 S3
S1 ？ ？ ？
S2 ？ ？ ？
S3 ？ ？ ？
S1 : rise
S2：decline
S3：calm
diff volume
10/1 -0.2 70000
10/2
ㄉ
0.1 69000
10/3 0.1 85000
… … …
diff volume
S1 S1-diff(μ, σ2) S1-volume(μ, σ2)
S2 S2-diff(μ, σ2) S2-volume(μ, σ2)
S3 S3-diff(μ, σ2) S3-volume(μ, σ2)
input : numbers of state & O
out put : A,B
predict next status
A B
O
?用問題3解出A,B，就可以?用問題2
去decode，求出預測結果](https://image.slidesharecdn.com/hmm-170325023436/85/Hidden-markov-model-25-320.jpg)
Hidden markov model
- 2. D6 D4 D8 1 2 3 4 5 6 1 2 3 4 1 2 3 5 6 7 4 8
- 3. 每?一次擲骰從三個骰?子中挑?一個，每?一個挑到的機率為1/3 挑到骰?子後開始擲，擲完結果記下，並且重覆挑骰再擲可得 1 6 3 5 2 1 6 3 5 2 - observation symbols 1 6 3 5 2 可能分別由 D6 D8 D8 D6 D4 擲出 D6 D8 D8 D6 D4 1 6 3 5 2 hidden state visible state
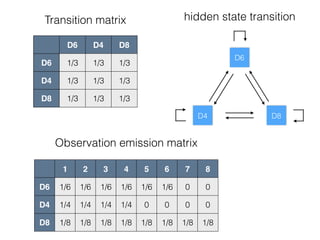
- 4. D6 D4 D8 hidden state transition D6 D4 D8 D6 1/3 1/3 1/3 D4 1/3 1/3 1/3 D8 1/3 1/3 1/3 1 2 3 4 5 6 7 8 D6 1/6 1/6 1/6 1/6 1/6 1/6 0 0 D4 1/4 1/4 1/4 1/4 0 0 0 0 D8 1/8 1/8 1/8 1/8 1/8 1/8 1/8 1/8 Transition matrix Observation emission matrix
- 5. Initial state distribution π = {πi} Number of states in the model X : N Number of observation symbols O : M Transition matrix A = {aij} , where aij represents the transition probability from state i to state j Observation emission matrix B = {bij} , where bij represent the probability of observation j at state i 幾個骰?子 3 觀察到骰出的點數 1-8 D4骰?子到D8骰?子的機率 1/3 D4骰?子出現1的機率 1/4 ?首次選骰?子的機率各 1/3
- 6. Three Fundamental Problems And Solutions For HMM 1. The Evaluation Problem - Forward 已知骰?子有幾種，每種骰?子是什麼，知道擲出來想 知道此結果的機率？ D6 D4 D8 D6 1/3 1/3 1/3 D4 1/3 1/3 1/3 D8 1/3 1/3 1/3 1 2 3 4 5 6 7 8 D6 1/6 1/6 1/6 1/6 1/6 1/6 0 0 D4 1/4 1/4 1/4 1/4 0 0 0 0 D8 1/8 1/8 1/8 1/8 1/8 1/8 1/8 1/8 求 1 6 3 5 2 的機率？
- 7. solution 1. The Evaluation Problem - Forward D6 D4 D6 1/2 1/2 D4 1/2 1/2 1 2 3 4 5 6 D6 1/6 1/6 1/6 1/6 1/6 1/6 D4 1/4 1/4 1/4 1/4 0 0 求 1 2 3的機率？ 1 2 3 D6 1/2*1/6 (1/2*1/6)*1/2*1/6 ＋ (1/2*1/4)*1/2*1/6 (5/288)*1/2*1/6 ＋ (5/192)*1/2*1/6 D4 1/2*1/4 (1/2*1/6)*1/2*1/4 ＋ (1/2*1/4)*1/2*1/4 (5/288)*1/2*1/4 ＋ (5/192)*1/2*1/4 A : 0.009
- 8. solution 1. The Evaluation Problem - Forward HMM parameter μ=(π,A,B) forward probability : αj(t) when time = t，observation sequence (o1,o2,…,ot)，the probability of hidden state j when t = 1 [ ]
- 9. Three Fundamental Problems And Solutions For HMM 2. The Decoding Problem - Viterbi 已知骰?子有幾種，每種骰?子是什麼，根據骰?子擲出 來的結果，想知道擲出來的是哪種骰?子？ D6 D4 D8 D6 1/3 1/3 1/3 D4 1/3 1/3 1/3 D8 1/3 1/3 1/3 1 2 3 4 5 6 7 8 D6 1/6 1/6 1/6 1/6 1/6 1/6 0 0 D4 1/4 1/4 1/4 1/4 0 0 0 0 D8 1/8 1/8 1/8 1/8 1/8 1/8 1/8 1/8 求1 6 3 5 2結果最?大可能的擲骰順序？ maybe D6 D8 D8 D6 D4
- 10. solution 2. The Decoding Problem - Viterbi 求 1 2 3最?大可能的擲骰順序？ 1/2*1/4 > 1/2*1/6 D4 (1/2*1/6)*1/2*1/6 + (1/2*1/4)*1/2*1/6 (1/2*1/6)*1/2*1/4 + (1/2*1/4)*1/2*1/4 > D4 (5/288)*1/2*1/6 + (5/192)*1/2*1/6 > (5/288)*1/2*1/4 + (5/192)*1/2*1/4 D4 A : D4 D4 D4 1 2 3 D6 1/2*1/6 (1/2*1/6)*1/2*1/6 ＋ (1/2*1/4)*1/2*1/6 (5/288)*1/2*1/6 ＋ (5/192)*1/2*1/6 D4 1/2*1/4 (1/2*1/6)*1/2*1/4 ＋ (1/2*1/4)*1/2*1/4 (5/288)*1/2*1/4 ＋ (5/192)*1/2*1/4
- 11. solution 2. The Decoding Problem - Viterbi when t = 1
- 12. Three Fundamental Problems And Solutions For HMM 3. The Learning Problem - Baum-Welch(EM algorithm) 已知骰?子有幾種，不知道骰?子是什麼，觀察多次骰 ?子擲出來的結果，想反推每種骰?子是什麼？ 1 6 3 5 2 2 5 7 1 2 4 5 5 6 1 3 4 5 6 8 1 2 3 4 5 6 7 8 D6 ? ? ? ? ? ? ? ? D4 ? ? ? ? ? ? ? ? D8 ? ? ? ? ? ? ? ? D6 D4 D8 D6 ？ ？ ？ D4 ？ ？ ？ D8 ？ ？ ？
- 13. solution 3. The Learning Problem - Baum-Welch(EM algorithm) 求 1 2 3 4 5 6 7 8 D6 ? ? ? ? ? ? ? ? D4 ? ? ? ? ? ? ? ? D8 ? ? ? ? ? ? ? ? D6 D4 D8 D6 ？ ？ ？ D4 ？ ？ ？ D8 ？ ？ ？ 初始挑骰?子機率 D6,D4,D8 ? Baum-Welch A1 B1 π1 假設 已知 1 6 3 5 2 2 5 7 1 2 4 5 5 6 1 3 4 5 6 8 A2 B2 π2 update An Bn πn 收斂 A B π
- 14. solution 3. The Learning Problem - Baum-Welch(EM algorithm) forward probability backward probability when t = T-1 when t = T
- 15. solution 3. The Learning Problem - Baum-Welch(EM algorithm) γj(t) : when time = t，the probability of hidden state j HMM parameter μ=(π,A,B) and observation sequence O ξij(t) : the probability of when time = t，the probability of hidden state i,when time = t+1，the probability of hidden state j
- 16. solution 3. The Learning Problem - Baum-Welch(EM algorithm) update HMM parameter
- 17. Initial state distribution π = {πi} Number of states in the model: N Number of observation symbols: M Transition matrix A = {aij} , where aij represents the transition probability from state i to state j Observation emission matrix B = {bj(Ot)} , where bj(Ot) represent the probability of observing Ot at state j 幾個骰?子 3 觀察到骰出的點數 1-8 D4骰?子到D8骰?子的機率 1/3 D4骰?子出現1的機率 1/4 ?首次選骰?子的機率各 1/3
- 18. The Evaluation Problem - Forward The Decoding Problem - Viterbi The Learning Problem - Baum-Welch 已知骰?子有幾種，每種骰?子是什麼，想知道擲出來 想知道此結果的機率？ 已知骰?子有幾種，每種骰?子是什麼，根據骰?子擲出 來的結果，想知道擲出來的是哪種骰?子？ 已知骰?子有幾種，不知道骰?子是什麼，觀察多次骰 ?子擲出來的結果，想反推每種骰?子是什麼？
- 20. S O Discrete Discrete S O Discrete Continuous S O Continuous Continuous D6 D8 1 6 Mixture of Multinomials Mixture of Gaussians Factor Analysis HMM HMM LDS
- 21. The Decoding Problem - Viterbi 中?文分詞 (jieba) states set : {B:begin, M:middle, E:end, S:single} 我天天去實驗室 SBESBME 我/天天/去/實驗室 S/BE/S/BME initiaState B 0.15 M 0.005 E 0.005 S 0.84 B M E S B 0 0.3 0.7 0 M 0 0.2 0.8 0 E 0.4 0 0 0.6 S 0.5 0 0 0.5 國 ?民 我 挺 柱 … B -8 -7 -6 -8 -7 … M -10 -9 -8 -10 -7 … E -8 -8 -6 -9 -7 … S -9 -8 -5 -7 -8 … 經驗法則，?用現有收集詞庫統計詞頻即可得知 S O Discrete Discrete 數字太?小經過log處理
- 22. The Learning Problem - Baum-Welch S O Discrete Continuous Gaussian HMM of stock data
- 23. mean μ Gaussian Normal Distribution variance σ2 probability density function :
- 24. S1 S2 S3 S1-diff(μ, σ2) S1-volume(μ, σ2) S2-diff(μ, σ2) S2-volume(μ, σ2) S3-diff(μ, σ2) S3-volume(μ, σ2) S = 3 O = 2 Gaussian = 3*2 = 6 如果每?一個S所噴出O的結果符合 gaussian normal distribution diff = close_v(today) - close_v(yesterday) volume = volume(today) O =[diff, volume] S1 : rise S2：decline S3：calm
- 25. S O Discrete Continuous Gaussian HMM of stock data diff = close_v(today) - close_v(yesterday) volume = volume(today) O =[diff, volume] S1 S2 S3 S1 ？ ？ ？ S2 ？ ？ ？ S3 ？ ？ ？ S1 : rise S2：decline S3：calm diff volume 10/1 -0.2 70000 10/2 ㄉ 0.1 69000 10/3 0.1 85000 … … … diff volume S1 S1-diff(μ, σ2) S1-volume(μ, σ2) S2 S2-diff(μ, σ2) S2-volume(μ, σ2) S3 S3-diff(μ, σ2) S3-volume(μ, σ2) input : numbers of state & O out put : A,B predict next status A B O ?用問題3解出A,B，就可以?用問題2 去decode，求出預測結果
- 26. BUT! 如果每?一個S所噴出O的結果符合 gaussian normal distribution
- 27. Gaussian Mixture Model GMM S -> O ?一個狀態S噴出的O對應?一個Gaussian S -> k -> O ?一個狀態S有k個管道，每個管道 噴出的O對應?一個Gaussian 1 2 3 ck × N( v , μ k , σ2 k ) N( v , μ , σ2 ) 多個Gaussian組成?一個GMM ?一個狀態S噴出的O 常態分佈 符合 不符合 Gaussian HMM GMM HMM
- 28. S1 S2 S3 S1-diff(μ, σ2) S1-volume(μ, σ2) S2-volume(μ, σ2) S3-volume(μ, σ2) S2-diff(μ, σ2) S3-diff(μ, σ2) 每?一個S所噴出O的結果符合GMM
- 29. g ng b nb g 0.6 0.1 0.2 0.1 ng 0.2 ? 0.3 0.2 b ? ? nb ? ? 定義 status gamer的層級 diff wi? S1 S1-diff(μ, σ2) 0.2 S2 S2-diff(μ, σ2) 0.4 S3 S3-diff(μ, σ2) 0.6 DiscreteContinuous 收集 O 觀察特徵 決定模型 S O Discrete Continuous MultinomialHMM S O Discrete Continuous GaussianHMM GMMHMM n_mix (注意 over?tting) boring的層級