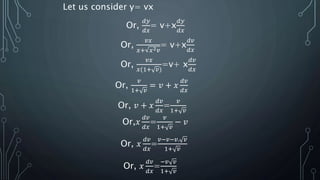Higher order math
- 2. MY PRESENTATION TOPIC IS HOMOGENEOUS NAME: PIAS AHMMED ID:151-15-5198
- 3. SOLVE THE FOLLOWING HOMOGENEOUS DE ððĶ ððĨ = ðĶ ðĨ+ ðĨðĶ Sol: The given DE is ððĶ ððĨ = ðĶ ðĨ+ ðĨðĶ Let, f(x,y)= ðĶ ðĨ+ ðĨðĶ f(tx,ty)=ðĄ0( ðĶ ðĨ+ ðĨðĶ ) =ðĄ0 ð(ðĨ, ðĶ) f(x , y) is a homogenous function of Zero degree. So the given DE is also a homogenous DE.
- 4. Let us consider y= vx Or, ððĶ ððĨ = v+x ððĶ ððĨ Or, ðĢðĨ ðĨ+ ðĨ2 ðĢ = v+x ððĢ ððĨ Or, ðĢðĨ ðĨ(1+ ðĢ) =v+ x ððĢ ððĨ Or, ðĢ 1+ ðĢ = ðĢ + ðĨ ððĢ ððĨ Or, ðĢ + ðĨ ððĢ ððĨ = ðĢ 1+ ðĢ Or,ðĨ ððĢ ððĨ = ðĢ 1+ ðĢ â ðĢ Or, ðĨ ððĢ ððĨ = ðĢâðĢâðĢ. ðĢ 1+ ðĢ Or, ðĨ ððĢ ððĨ = âðĢ ðĢ 1+ ðĢ
- 5. Separating the variables and integrating Or, ( 1+ ðĢ âðĢ. ðĢ )ððĢ= 1 ðĨ ððĨ Or,( 1 âðĢ ðĢ â ðĢ ðĢ ðĢ )ððĢ= 1 ðĨ ððĨ Or, 1 âðĢ ðĢ ððĢ â 1 ðĢ ððĢ= 1 ðĨ ððĨ Or, 1ððĢ â 1 ðĢ ððĢ= 1 ðĨ ððĨ Or, -v-lnv=lnx Or, -v=lnvx Or,- ðĶ ðĨ =lny