Hiperbola - Irisan Kerucut
Download as PPTX, PDF1 like1,475 views
Menjelaskan definisi, jenis, dan rumus yang berhubungan dengan Hiperbola yang termasuk irisan kerucut
More Related Content
What's hot (20)
Viewers also liked (7)
Similar to Hiperbola - Irisan Kerucut (20)
Recently uploaded (20)
Hiperbola - Irisan Kerucut
- 1. Hiperbola Kelompok 3 Rizka Dwie Suci Wulandari Sarah Tsabitha Natasha B Theresia Dwianita S Vega Mylanda XI MIA 5 SMA Negeri 98 Jakarta
- 2. Hiperbola adalah tempat kedudukan titik-titik yang selisih jaraknya terhadap dua titik tertentu adalah tetap.
- 3. 2 2- 2 2 = 1
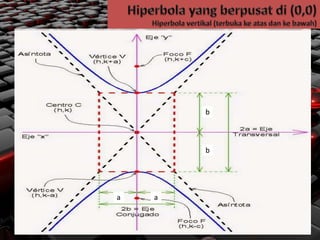
- 4. b b a a
- 5. 2 2- 2 2 = 1 Fokus = f1 (0,-c) dan f2 (0,c) Puncak = V1 (0,-b) dan V2 (0,b) Panjang sumbu sekawan = 2a Panjang Sumbu melintang = 2b Persamaannya = Latus Rectum = L = Eksentris ( e = = = Asimtot = y = 賊 x Fokus = f1 (-c, 0) dan f2 (c, 0) Puncak = V1 (-a, 0) dan V2 (a,0) Panjang sumbu sekawan = 2b Panjang Sumbu melintang = 2a Persamaannya = Latus Rectum = L = Eksentris ( e = = = Asimtot = y = 賊 x 2 2
- 6. Hiperbola Horizontal e = = = 2 Hiperbola Vertikal e= = = 2 Hiperbola Horizontal y = 賊 x Hiperbola Vertikal y = 賊 x
- 7. - = 1 Titik fokus : (h-c,k) dan (h+c,k) Titik puncak (h-a,k) dan (h+a,k) Panjang sumbu melintang = 2a Panjang sumbu sekawan = 2b Panjang Latus rectum = Eksentrisitas e = Asimtot : y-k = 賊 (x-h) Persamaan:
- 8. - = 1 Titik fokus : (h, k-c) dan (h,k+c) Titik puncak : (h, k-a) dan (h,k+a) Panjang sumbu melintang = 2b Panjang sumbu sekawan = 2a Panjang Latus rektum = Eksentrisitas e = Asimtot : y-k = 賊 (x-h) Persamaan:
- 9. 1. Tentukan kedua titik fokus dari hiperbola : Jawab : jika kita melihat persamaan umumnya, maka kita peroleh a=4 dan b=3. dan kita dapatkan c=5. Sehingga koordinat titik fokus dari hiperbola tersebut adalah F1 (-5,0) (5,0)
- 10. 2. Tentukan garis asimtot dari hiperbola : Jawab : => Hiperbola Horizontal jika kita melihat persamaan umumnya, maka kita peroleh a=4 dan b=3. Kedua asimtotnya kita kenal sebagai , ,maka kita peroleh kedua asimtotnya adalah
- 11. 3. Panjang sumbu melintang dan sumbu sekawan dari suatu Hiperbola sama dengan 10 dan 6. Jika Hiperbola berpusat di (0,0) dan sumbu melintang berimpit dengan Sumbu y maka persamaan Hiperbola adalah... Jawab : Panjang sumbu melintang adalah = 2.b, jadi : 10 = 2.b b = 5 Panjang sumbu sekawan adalah = 2.a, jadi : 6 = 2.a a = 3 b2 = 25 b = 5 ; a2 = 9 a = 3 Jadi, jawabannya adalah
- 12. 1. Panjang sumbu melintang dan sumbu sekawan dari suatu hiperbola sama dengan 6 dan 4. jika hiperbola berpusat di (0,0) dan sumbu melintang berimpit dengan sumbu x maka persamaan hiperbola adalah... 2. Panjang latus rectum dari hiperbola dengan persamaan diatas adalah...... 3. Persamaan asimtot hiperbola pada persamaan diatas adalah ...