Homomorphic Encryption
Download as pptx, pdf2 likes4,401 views
Homomorphic encryption allows computations to be carried out on encrypted data without decrypting it first. This summary discusses Craig Gentry's scheme for fully homomorphic encryption based on ideal lattices. The scheme works by encrypting bits as ciphertexts with small noise that grows with computations. A bootstrapping procedure called re-crypt reduces the noise to keep ciphertexts decryptable. While promising for applications like cloud computing, the scheme has high computational costs that scale poorly with security level. Current research aims to make homomorphic encryption more efficient and practical.
1 of 20
Downloaded 285 times







![Craig Gentry scheme (integers)
âą Key: odd integer p > 2N
âą Encryption algorithm: given a bit b -> E(b) = c = b +
2x + kp, where x is in [-n/2,n/2] and k is an integer
chosen from some range
âą Decryption algorithm: b = (c mod p) mod 2, where (c
mod p) is the noise and belongs to [-n,n]
âą Decryption works if b + 2x â [-N,N] â[-p/2,p/2]](https://image.slidesharecdn.com/homomorphic-130320052226-phpapp01/85/Homomorphic-Encryption-9-320.jpg)
![Craig Gentry scheme (integers)
âą Graig Gentry schemeâs homomorphic assumptions
â Addiction: c1 + c2 = b1+ b2 + 2(x1+x2) + (k1+k2)p =
b1 xor b2 + 2x + kp
âą Decryption works if (b1+2x1) + (b2+2x2) is in [-
N,N]
â Multiplication: c1*c2 = b1*b2 + 2(b1x2 + b2x1 +
2x1x2) + kp = b1*b2 + 2x + kp
âą Decryption works if (b1+2x1) * (b2+2x2) is in [-
N,N]](https://image.slidesharecdn.com/homomorphic-130320052226-phpapp01/85/Homomorphic-Encryption-10-320.jpg)










Ad
Recommended
Homomorphic Encryption
Homomorphic EncryptionGöktuÄ Serez
Ìę
Homomorphic encryption allows computations to be performed on encrypted data without decrypting it first. This document discusses homomorphic encryption techniques including partially homomorphic encryptions that support either addition or multiplication operations, and fully homomorphic encryption introduced by Craig Gentry that supports both types of operations. It also covers the use of ideal lattices in lattice-based cryptosystems and the bootstrapping technique used to "refresh" ciphertexts and prevent noise from accumulating during homomorphic computations.Homomorphic encryption
Homomorphic encryptionNamit Sinha
Ìę
Homomorphic encryption allows computations to be carried out on encrypted data without decrypting it first. It preserves relationships between encrypted elements. Traditional encryption requires decrypting data before computations, but homomorphic encryption allows a third party to perform operations on encrypted data. While partially homomorphic encryption allows some operations like addition or multiplication, fully homomorphic encryption would allow any computation. Applications include encrypted database querying, secure voting systems, and protecting proprietary algorithms. Current research aims to develop practical applications by 2015.Homomorphic encryption
Homomorphic encryptionCysinfo Cyber Security Community
Ìę
This document provides an overview of homomorphic encryption. It begins by defining homomorphic encryption as a form of encryption that allows specific types of computations to be performed on ciphertext and generate an encrypted result that matches the operations performed on the plaintext when decrypted. It then discusses different types of homomorphic encryption including partially homomorphic (additive or multiplicative), fully homomorphic encryption, and provides examples like RSA, ElGamal, and Paillier. The document concludes by listing some applications of homomorphic encryption such as e-voting, biometric verification, and discusses Paillier encryption specifically.Introduction to Homomorphic Encryption
Introduction to Homomorphic EncryptionChristoph Matthies
Ìę
The document discusses homomorphic encryption, which allows computations on encrypted data without needing to decrypt it first. It explores various applications, such as secure medical record analysis and spam filtering, and contrasts different homomorphic encryption schemes, highlighting their strengths and weaknesses. Practical examples are provided, including the RSA encryption method's homomorphic property and circuit encryption techniques.Homomorphic Encryption
Homomorphic EncryptionVipin Tejwani
Ìę
The document discusses homomorphic encryption, which allows computations to be performed on encrypted data and obtain an encrypted result without decrypting the inputs. It provides examples of partially homomorphic encryption schemes like RSA that allow only addition or multiplication, and fully homomorphic encryption introduced by Craig Gentry in 2009 that allows any computation. The document also discusses applications of homomorphic encryption like secure cloud computing and processing of sensitive encrypted medical records. It summarizes Craig Gentry's homomorphic encryption scheme and the HELib software library implementation.Homomorphic encryption on Blockchain Principles
Homomorphic encryption on Blockchain PrinciplesJohann Höchtl
Ìę
The document discusses homomorphic encryption and secure multiparty computation. Homomorphic encryption allows computations to be performed on encrypted data and obtain an encrypted result without decrypting the data. This allows data to be processed privately. Secure multiparty computation allows distributed parties to jointly compute a function over their private inputs while revealing nothing but the output. Implementations like SPDZ and Enigma aim to perform computations across blockchain networks to allow private analytics on distributed data. Homomorphic encryption accumulates noise with operations, limiting computations, while secure multiparty computation requires rewriting programs to handle control flows and conditionals.Elliptical curve cryptography
Elliptical curve cryptographyBarani Tharan
Ìę
The document presents an overview of elliptic curve cryptography (ECC), including its introduction, applications, and mathematical foundations. It describes how ECC functions in public-key cryptosystems, comparing it to RSA and DIS methods, and illustrates key generation, encryption, and decryption processes using elliptic curves. Additionally, the document discusses the advantages of ECC in terms of security and efficiency, particularly for devices with limited resources.Cryptography
CryptographyJens Patel
Ìę
This document provides an overview of cryptography. It defines cryptography as the science of secret writing and discusses its use in applications like ATM cards and passwords. It describes the basic components of cryptography including plaintext, ciphertext, ciphers, keys, and algorithms. It differentiates between symmetric and asymmetric key cryptography. It provides examples of traditional and modern ciphers, including DES, AES, and RSA algorithms. In conclusion, it states that cryptography techniques help maintain data security, privacy, and integrity.Fundamentals of cryptography
Fundamentals of cryptographyHossain Md Shakhawat
Ìę
The document provides an overview of cryptography, detailing its definition, historical development, and the processes of encryption and decryption. It explains key concepts including symmetric and asymmetric cryptography, the importance of confidentiality, integrity, authentication, and non-repudiation, as well as various cryptographic algorithms and attacks. The document emphasizes the role of cryptography in secure communication and its applications in modern technology.Lesson 1- Foundation of Cryptology
Lesson 1- Foundation of CryptologyMLG College of Learning, Inc
Ìę
The document provides an overview of cryptography and cryptanalysis. It discusses the history and foundations of cryptology, including definitions of key terms. Symmetric and asymmetric encryption algorithms are described, such as DES, AES, RSA, and their uses of secret or public keys. The importance of key size for encryption strength is also noted. Cryptographic methods like substitution, transposition, XOR, Vernam, and hash ciphers are outlined.Cryptography ppt
Cryptography pptAnubhav Sokhal
Ìę
This document discusses cryptography, which is the science of secure communication. It covers the basics of cryptography including its objectives, components, terminology, types, and advantages. Specifically, it explains how cryptography ensures confidentiality, integrity, and authentication of information. It also discusses symmetric and asymmetric encryption methods. Symmetric encryption uses a shared key for encryption and decryption while asymmetric encryption uses public and private key pairs. The document highlights how cryptography provides secure communication methods and is important for both military and everyday applications.Cryptography - 101
Cryptography - 101n|u - The Open Security Community
Ìę
This document provides an overview of cryptography concepts including symmetric and asymmetric key algorithms, cryptographic hashes, and tools for cryptanalysis. It defines common terminology like plaintext, ciphertext, encryption, and decryption. Symmetric algorithms discussed include the Vernam cipher, A5/1, DES, AES, and RC4. Asymmetric algorithms covered are RSA and Diffie-Hellman key exchange. Cryptographic hashes like MD5 and SHA-1 are also summarized along with resources for cryptanalysis.I mage encryption using rc5
I mage encryption using rc5Suramrit Singh
Ìę
RC5 is a symmetric block cipher algorithm developed by Ronald Rivest. It can encrypt digital images by dividing the image into blocks and encrypting each block using the RC5 algorithm. RC5 is suitable for image encryption because it uses data-dependent rotations, which helps prevent attacks. When encrypting images with RC5, the image is treated as a stream of bits that are encrypted in blocks using the RC5 algorithm and an expanded key. The encrypted image is evaluated based on factors like visual inspection, pixel value deviation, entropy, correlation and avalanche effect to determine the security and effectiveness of the encryption. Evaluation shows RC5 encryption produces images that look random and have high security.Cryptography
Cryptographygueste4c97e
Ìę
Cryptography involves secret writing and encrypting messages so that only authorized parties can read them. It uses algorithms and keys to encrypt plaintext into ciphertext. Cryptanalysis involves breaking ciphers, while cryptography is designing ciphers. Cryptology encompasses both cryptography and cryptanalysis. Common encryption models involve plaintext being encrypted into ciphertext using a key, which is then transmitted and decrypted by the intended receiver using the same key.Cryptography using rsa cryptosystem
Cryptography using rsa cryptosystemSamdish Arora
Ìę
The document covers cryptography and its importance, particularly focusing on the RSA cryptosystem, a public key cryptosystem developed in 1976. It explains the mathematical foundations behind RSA, including Euclid's algorithm, modulo arithmetic, and Euler's theorem, and outlines the process for generating keys and encrypting/decrypting messages. It emphasizes the role of cryptography in securing electronic transactions and communication in modern technology.Unit 3
Unit 3KRAMANJANEYULU1
Ìę
This document provides an overview of number theory and its applications to asymmetric key cryptography. It begins with definitions of prime numbers, relatively prime numbers, and modular arithmetic. It then covers the Euclidean algorithm for finding the greatest common divisor of two numbers, Fermat's and Euler's theorems, and the Chinese Remainder Theorem. The document concludes with an introduction to public key cryptography, including the basic principles, requirements, and the RSA algorithm as a widely used example of an asymmetric encryption scheme.Rsa cryptosystem
Rsa cryptosystemAbhishek Gautam
Ìę
The presentation discusses the RSA cryptosystem, a widely used public key cryptography method that provides secure communication by utilizing pairs of keys: a public key for encryption and a private key for decryption. Key concepts such as plaintext, ciphertext, and modular arithmetic are explained, alongside the process of key generation and the encryption/decryption algorithms. The RSA algorithm's reliance on mathematical principles and its applications in network security are also highlighted, along with potential vulnerabilities and the importance of key size for security.MAC-Message Authentication Codes
MAC-Message Authentication CodesDarshanPatil82
Ìę
The document outlines the requirements and functions of message authentication codes (MACs) and their role in verifying message integrity and authenticity. It details various potential attacks on message integrity, such as disclosure, masquerade, and timing modifications, and introduces digital signatures as a countermeasure. Additionally, it covers the construction and security of MACs, including brute-force attacks and cryptanalysis, while presenting HMAC as a standard for implementing MAC with existing hash functions.Cryptography and network security Nit701
Cryptography and network security Nit701Amit Pathak
Ìę
The document provides an extensive overview of cryptography and network security, covering various types of cryptography, key algorithms, and their applications in securing communication. It discusses both symmetric and asymmetric cryptography, detailing their mechanisms, advantages, and drawbacks. Key concepts such as encryption, decryption, and cryptographic services like confidentiality, integrity, and authentication are also articulated, alongside various algorithms including RSA and DES.Public Key Cryptography and RSA algorithm
Public Key Cryptography and RSA algorithmIndra97065
Ìę
The document presents an overview of public key cryptography and the RSA algorithm, detailing the principles of encryption and decryption, the distinction between symmetric and asymmetric key cryptography, and the mathematical foundations of RSA. It describes the RSA algorithm's steps for key generation, encryption, and decryption, and discusses its practical applications in securing web traffic, emails, and remote connections. Despite RSA's popularity and advantages in security, it faces challenges such as slow key generation and decryption compared to symmetric key systems like DES.Steganography
SteganographyDaksh Verma
Ìę
The document discusses image steganography techniques. It begins by defining steganography as concealed writing and distinguishing it from cryptography. It then describes the basic process of embedding a secret message into a cover image to produce a stego-image. Different embedding algorithms are presented, including Least Significant Bit substitution and LSB with randomization. Histograms are used to analyze the differences between cover and stego-images. The document concludes by discussing attackers and techniques to improve robustness, such as LSB matching and Mielikainen's improved LSB matching method. symmetric key encryption algorithms
symmetric key encryption algorithmsRashmi Burugupalli
Ìę
Symmetric Key Encryption Algorithms can be categorized as stream ciphers or block ciphers. Block ciphers like the Data Encryption Standard (DES) operate on fixed-length blocks of bits, while stream ciphers process messages bit-by-bit. DES is an example of a block cipher that encrypts 64-bit blocks using a 56-bit key. International Data Encryption Algorithm (IDEA) is another block cipher that uses a 128-bit key and 64-bit blocks, employing addition and multiplication instead of XOR like DES. IDEA consists of 8 encryption rounds followed by an output transformation to generate the ciphertext from the plaintext and key.Introduction to Cryptography
Introduction to CryptographyBharat Kumar Katur
Ìę
This document provides an overview of cryptography concepts including encryption, decryption, symmetric and asymmetric cryptosystems. It discusses X.509 certificates, self-signed certificates, and why certificates need to be signed by a Certificate Authority. It also covers RSA and AES cryptosystems, OpenSSL functions for X509, EVP and RSA, and hybrid cryptosystems.How to Share a Secret
How to Share a SecretKelum Senanayake
Ìę
The document discusses Adi Shamir's contributions to cryptography, specifically his secret-sharing scheme which allows a secret to be divided into pieces that can only be reconstructed with a certain number of those pieces. It emphasizes the impracticality of key management scenarios and introduces a threshold scheme where knowledge of a subset of pieces enables the secret's reconstruction while preventing access through fewer pieces. The scheme provides security, flexibility, and efficiency in organizations, ensuring that important secrets are safeguarded effectively.CryptographieSeifallah Jardak
Ìę
Le document traite de la cryptographie et du hachage, expliquant les types de cryptage symétrique et asymétrique ainsi que les algorithmes associés. Il aborde également les propriétés des algorithmes de hachage, leur utilité, la notion de collision et les méthodes de craquage. Enfin, des recommandations sont faites sur la sécurisation des mots de passe.Elgamal digital signature
Elgamal digital signatureMDKAWSARAHMEDSAGAR
Ìę
The ElGamal digital signature scheme was described by Tahir Elgamal in 1985. It uses a key pair consisting of a public key and private key, where the private key is used to generate signatures and the public key is used to verify signatures. Signatures provide message authentication, integrity, and non-repudiation by proving the message was signed by the private key holder. The document then proceeds to describe the technical process of generating keys, signing messages, and verifying signatures using ElGamal signatures with an example.Post Quantum Cryptography: Technical Overview
Post Quantum Cryptography: Technical OverviewRamesh Nagappan
Ìę
The document provides a comprehensive overview of post-quantum cryptography, comparing classical and quantum computing, and highlighting the vulnerabilities traditional encryption faces against quantum algorithms like Shor's and Grover's. It discusses the need for post-quantum cryptography (PQC) and quantum key distribution (QKD) as methods to secure communications against quantum attacks, detailing various quantum-resistant algorithms. Additionally, it reviews ongoing efforts for standardization in the realm of post-quantum cryptography through initiatives by NIST and ETSI.Broadcasting and low exponent rsa attack
Broadcasting and low exponent rsa attackAnkita Kapratwar
Ìę
1) The document describes how to decrypt an RSA ciphertext using a Chinese Remainder Theorem attack when the public exponent is small. It involves using the public moduli and exponents from certificates to determine the plaintext.
2) The attack works by using the Chinese Remainder Theorem to determine the plaintext from the ciphertexts modulo the public moduli. This works because the public exponent is small, in this case 3, allowing extraction of the plaintext cube root.
3) Pseudocode is provided showing the steps: using the Chinese Remainder Theorem formula to combine the ciphertexts modulo the public moduli, taking the cube root to obtain the plaintext, which in this example decrypts to a German message about a fixedClass3
Class3ankitasinghbsc
Ìę
This document provides an overview of cryptography concepts including:
- Homework 1 is due on 1/18 and project 1 is due the next day
- It reviews classical ciphers, modern symmetric ciphers like DES, and basic cryptography terminology
- It describes the Feistel cipher structure used in DES, the DES algorithm details like key scheduling and rounds, and strengths and weaknesses of DES versus alternatives like AES and triple DESComputing on Encrypted Data
Computing on Encrypted DataNew York Technology Council
Ìę
The document discusses the concept of computing on encrypted data, allowing for processing without revealing the data itself. It covers techniques such as homomorphic encryption, which enables the computation of arbitrary functions on encrypted data, and outlines the steps required to achieve this. Challenges related to performance and the practicality of current solutions are also highlighted, with suggestions for potential applications and improvements.More Related Content
What's hot (20)
Fundamentals of cryptography
Fundamentals of cryptographyHossain Md Shakhawat
Ìę
The document provides an overview of cryptography, detailing its definition, historical development, and the processes of encryption and decryption. It explains key concepts including symmetric and asymmetric cryptography, the importance of confidentiality, integrity, authentication, and non-repudiation, as well as various cryptographic algorithms and attacks. The document emphasizes the role of cryptography in secure communication and its applications in modern technology.Lesson 1- Foundation of Cryptology
Lesson 1- Foundation of CryptologyMLG College of Learning, Inc
Ìę
The document provides an overview of cryptography and cryptanalysis. It discusses the history and foundations of cryptology, including definitions of key terms. Symmetric and asymmetric encryption algorithms are described, such as DES, AES, RSA, and their uses of secret or public keys. The importance of key size for encryption strength is also noted. Cryptographic methods like substitution, transposition, XOR, Vernam, and hash ciphers are outlined.Cryptography ppt
Cryptography pptAnubhav Sokhal
Ìę
This document discusses cryptography, which is the science of secure communication. It covers the basics of cryptography including its objectives, components, terminology, types, and advantages. Specifically, it explains how cryptography ensures confidentiality, integrity, and authentication of information. It also discusses symmetric and asymmetric encryption methods. Symmetric encryption uses a shared key for encryption and decryption while asymmetric encryption uses public and private key pairs. The document highlights how cryptography provides secure communication methods and is important for both military and everyday applications.Cryptography - 101
Cryptography - 101n|u - The Open Security Community
Ìę
This document provides an overview of cryptography concepts including symmetric and asymmetric key algorithms, cryptographic hashes, and tools for cryptanalysis. It defines common terminology like plaintext, ciphertext, encryption, and decryption. Symmetric algorithms discussed include the Vernam cipher, A5/1, DES, AES, and RC4. Asymmetric algorithms covered are RSA and Diffie-Hellman key exchange. Cryptographic hashes like MD5 and SHA-1 are also summarized along with resources for cryptanalysis.I mage encryption using rc5
I mage encryption using rc5Suramrit Singh
Ìę
RC5 is a symmetric block cipher algorithm developed by Ronald Rivest. It can encrypt digital images by dividing the image into blocks and encrypting each block using the RC5 algorithm. RC5 is suitable for image encryption because it uses data-dependent rotations, which helps prevent attacks. When encrypting images with RC5, the image is treated as a stream of bits that are encrypted in blocks using the RC5 algorithm and an expanded key. The encrypted image is evaluated based on factors like visual inspection, pixel value deviation, entropy, correlation and avalanche effect to determine the security and effectiveness of the encryption. Evaluation shows RC5 encryption produces images that look random and have high security.Cryptography
Cryptographygueste4c97e
Ìę
Cryptography involves secret writing and encrypting messages so that only authorized parties can read them. It uses algorithms and keys to encrypt plaintext into ciphertext. Cryptanalysis involves breaking ciphers, while cryptography is designing ciphers. Cryptology encompasses both cryptography and cryptanalysis. Common encryption models involve plaintext being encrypted into ciphertext using a key, which is then transmitted and decrypted by the intended receiver using the same key.Cryptography using rsa cryptosystem
Cryptography using rsa cryptosystemSamdish Arora
Ìę
The document covers cryptography and its importance, particularly focusing on the RSA cryptosystem, a public key cryptosystem developed in 1976. It explains the mathematical foundations behind RSA, including Euclid's algorithm, modulo arithmetic, and Euler's theorem, and outlines the process for generating keys and encrypting/decrypting messages. It emphasizes the role of cryptography in securing electronic transactions and communication in modern technology.Unit 3
Unit 3KRAMANJANEYULU1
Ìę
This document provides an overview of number theory and its applications to asymmetric key cryptography. It begins with definitions of prime numbers, relatively prime numbers, and modular arithmetic. It then covers the Euclidean algorithm for finding the greatest common divisor of two numbers, Fermat's and Euler's theorems, and the Chinese Remainder Theorem. The document concludes with an introduction to public key cryptography, including the basic principles, requirements, and the RSA algorithm as a widely used example of an asymmetric encryption scheme.Rsa cryptosystem
Rsa cryptosystemAbhishek Gautam
Ìę
The presentation discusses the RSA cryptosystem, a widely used public key cryptography method that provides secure communication by utilizing pairs of keys: a public key for encryption and a private key for decryption. Key concepts such as plaintext, ciphertext, and modular arithmetic are explained, alongside the process of key generation and the encryption/decryption algorithms. The RSA algorithm's reliance on mathematical principles and its applications in network security are also highlighted, along with potential vulnerabilities and the importance of key size for security.MAC-Message Authentication Codes
MAC-Message Authentication CodesDarshanPatil82
Ìę
The document outlines the requirements and functions of message authentication codes (MACs) and their role in verifying message integrity and authenticity. It details various potential attacks on message integrity, such as disclosure, masquerade, and timing modifications, and introduces digital signatures as a countermeasure. Additionally, it covers the construction and security of MACs, including brute-force attacks and cryptanalysis, while presenting HMAC as a standard for implementing MAC with existing hash functions.Cryptography and network security Nit701
Cryptography and network security Nit701Amit Pathak
Ìę
The document provides an extensive overview of cryptography and network security, covering various types of cryptography, key algorithms, and their applications in securing communication. It discusses both symmetric and asymmetric cryptography, detailing their mechanisms, advantages, and drawbacks. Key concepts such as encryption, decryption, and cryptographic services like confidentiality, integrity, and authentication are also articulated, alongside various algorithms including RSA and DES.Public Key Cryptography and RSA algorithm
Public Key Cryptography and RSA algorithmIndra97065
Ìę
The document presents an overview of public key cryptography and the RSA algorithm, detailing the principles of encryption and decryption, the distinction between symmetric and asymmetric key cryptography, and the mathematical foundations of RSA. It describes the RSA algorithm's steps for key generation, encryption, and decryption, and discusses its practical applications in securing web traffic, emails, and remote connections. Despite RSA's popularity and advantages in security, it faces challenges such as slow key generation and decryption compared to symmetric key systems like DES.Steganography
SteganographyDaksh Verma
Ìę
The document discusses image steganography techniques. It begins by defining steganography as concealed writing and distinguishing it from cryptography. It then describes the basic process of embedding a secret message into a cover image to produce a stego-image. Different embedding algorithms are presented, including Least Significant Bit substitution and LSB with randomization. Histograms are used to analyze the differences between cover and stego-images. The document concludes by discussing attackers and techniques to improve robustness, such as LSB matching and Mielikainen's improved LSB matching method. symmetric key encryption algorithms
symmetric key encryption algorithmsRashmi Burugupalli
Ìę
Symmetric Key Encryption Algorithms can be categorized as stream ciphers or block ciphers. Block ciphers like the Data Encryption Standard (DES) operate on fixed-length blocks of bits, while stream ciphers process messages bit-by-bit. DES is an example of a block cipher that encrypts 64-bit blocks using a 56-bit key. International Data Encryption Algorithm (IDEA) is another block cipher that uses a 128-bit key and 64-bit blocks, employing addition and multiplication instead of XOR like DES. IDEA consists of 8 encryption rounds followed by an output transformation to generate the ciphertext from the plaintext and key.Introduction to Cryptography
Introduction to CryptographyBharat Kumar Katur
Ìę
This document provides an overview of cryptography concepts including encryption, decryption, symmetric and asymmetric cryptosystems. It discusses X.509 certificates, self-signed certificates, and why certificates need to be signed by a Certificate Authority. It also covers RSA and AES cryptosystems, OpenSSL functions for X509, EVP and RSA, and hybrid cryptosystems.How to Share a Secret
How to Share a SecretKelum Senanayake
Ìę
The document discusses Adi Shamir's contributions to cryptography, specifically his secret-sharing scheme which allows a secret to be divided into pieces that can only be reconstructed with a certain number of those pieces. It emphasizes the impracticality of key management scenarios and introduces a threshold scheme where knowledge of a subset of pieces enables the secret's reconstruction while preventing access through fewer pieces. The scheme provides security, flexibility, and efficiency in organizations, ensuring that important secrets are safeguarded effectively.CryptographieSeifallah Jardak
Ìę
Le document traite de la cryptographie et du hachage, expliquant les types de cryptage symétrique et asymétrique ainsi que les algorithmes associés. Il aborde également les propriétés des algorithmes de hachage, leur utilité, la notion de collision et les méthodes de craquage. Enfin, des recommandations sont faites sur la sécurisation des mots de passe.Elgamal digital signature
Elgamal digital signatureMDKAWSARAHMEDSAGAR
Ìę
The ElGamal digital signature scheme was described by Tahir Elgamal in 1985. It uses a key pair consisting of a public key and private key, where the private key is used to generate signatures and the public key is used to verify signatures. Signatures provide message authentication, integrity, and non-repudiation by proving the message was signed by the private key holder. The document then proceeds to describe the technical process of generating keys, signing messages, and verifying signatures using ElGamal signatures with an example.Post Quantum Cryptography: Technical Overview
Post Quantum Cryptography: Technical OverviewRamesh Nagappan
Ìę
The document provides a comprehensive overview of post-quantum cryptography, comparing classical and quantum computing, and highlighting the vulnerabilities traditional encryption faces against quantum algorithms like Shor's and Grover's. It discusses the need for post-quantum cryptography (PQC) and quantum key distribution (QKD) as methods to secure communications against quantum attacks, detailing various quantum-resistant algorithms. Additionally, it reviews ongoing efforts for standardization in the realm of post-quantum cryptography through initiatives by NIST and ETSI.Broadcasting and low exponent rsa attack
Broadcasting and low exponent rsa attackAnkita Kapratwar
Ìę
1) The document describes how to decrypt an RSA ciphertext using a Chinese Remainder Theorem attack when the public exponent is small. It involves using the public moduli and exponents from certificates to determine the plaintext.
2) The attack works by using the Chinese Remainder Theorem to determine the plaintext from the ciphertexts modulo the public moduli. This works because the public exponent is small, in this case 3, allowing extraction of the plaintext cube root.
3) Pseudocode is provided showing the steps: using the Chinese Remainder Theorem formula to combine the ciphertexts modulo the public moduli, taking the cube root to obtain the plaintext, which in this example decrypts to a German message about a fixedSimilar to Homomorphic Encryption (20)
Class3
Class3ankitasinghbsc
Ìę
This document provides an overview of cryptography concepts including:
- Homework 1 is due on 1/18 and project 1 is due the next day
- It reviews classical ciphers, modern symmetric ciphers like DES, and basic cryptography terminology
- It describes the Feistel cipher structure used in DES, the DES algorithm details like key scheduling and rounds, and strengths and weaknesses of DES versus alternatives like AES and triple DESComputing on Encrypted Data
Computing on Encrypted DataNew York Technology Council
Ìę
The document discusses the concept of computing on encrypted data, allowing for processing without revealing the data itself. It covers techniques such as homomorphic encryption, which enables the computation of arbitrary functions on encrypted data, and outlines the steps required to achieve this. Challenges related to performance and the practicality of current solutions are also highlighted, with suggestions for potential applications and improvements.Number Theory and Its Applications in Cryptography
Number Theory and Its Applications in Cryptographykapilhande1
Ìę
The document discusses the fundamentals of number theory and its applications in cryptography, detailing concepts such as modular arithmetic, encryption/decryption processes, and algorithms including RSA. It emphasizes the significance of number theory in securing data transmission and storage, alongside the importance of prime numbers and the Euler totient function in cryptographic algorithms. The conclusion highlights the role of randomness and the necessity of choosing large prime numbers for effective cryptographic systems.Dynamic Programming Matrix Chain Multiplication
Dynamic Programming Matrix Chain MultiplicationKrishnakoumarC
Ìę
The document discusses dynamic programming with a focus on matrix chain multiplication as an optimization problem. It explains how to efficiently determine the sequence of matrix multiplications required to minimize the total number of operations, emphasizing the importance of subproblem optimality and overlap. Additionally, it outlines a dynamic programming algorithm that computes the optimal parenthesization bottom-up, resulting in a time complexity of O(n^3).Public_Key_Cryptography in crypto analysis.ppt
Public_Key_Cryptography in crypto analysis.pptImmanImman6
Ìę
This document provides an overview of public key cryptography and algorithms such as Diffie-Hellman and RSA. It discusses symmetric ciphers which use a shared private key, and asymmetric ciphers which use public and private key pairs. The Diffie-Hellman key exchange algorithm allows secure key exchange over insecure channels. RSA encryption is based on the difficulty of factoring large numbers and uses a public key for encryption and private key for decryption. The document also notes some moral issues around information theft and privacy in cryptography."Mesh of Periodic Minimal Surfaces in CGAL."
"Mesh of Periodic Minimal Surfaces in CGAL."Vissarion Fisikopoulos
Ìę
The document discusses meshing periodic surfaces in CGAL. It describes adapting the CGAL surface meshing algorithm to work with periodic triangulations by modifying point insertion and refinement criteria. Examples meshing various periodic minimal surfaces like the gyroid and schwarz P surface are shown for different criteria values. Future work includes improving the refinement criteria to handle all cases and proving algorithm correctness and termination.parameterized complexity for graph Motif
parameterized complexity for graph MotifAMR koura
Ìę
The document summarizes research on the parameterized complexity of the graph MOTIF problem. It begins by defining the problem and providing an example. It then discusses how graph MOTIF can be solved efficiently using different parameters, such as cluster editing, distance to clique, and vertex cover number. The document also analyzes parameters for which graph MOTIF remains NP-hard, such as the deletion set number parameter. In conclusion, it provides references for the algorithms and results discussed.Elliptic curve cryptography and zero knowledge proof
Elliptic curve cryptography and zero knowledge proofNimish Joseph
Ìę
This document discusses elliptic curve cryptography and zero knowledge proofs. It begins by establishing the mathematical foundations needed for cryptography, including groups, rings, fields, and the discrete logarithm problem. It then explains how elliptic curves can be used in public key cryptography applications like Diffie-Hellman key exchange and ElGamal encryption. It also covers zero knowledge proofs, their properties, examples of uses, and the Fiat-Shamir identification protocol. Throughout, it provides examples to illustrate key concepts in elliptic curve cryptography and zero knowledge proofs.Elliptic Curve Cryptography and Zero Knowledge Proof
Elliptic Curve Cryptography and Zero Knowledge ProofArunanand Ta
Ìę
The document covers elliptic curve cryptography (ECC) and zero knowledge proofs (ZKP), exploring their mathematical foundations, applications in public key cryptography, and efficiencies compared to traditional methods like RSA. It introduces key concepts such as group structures, discrete logarithm problems, and the implementation of ECC in various systems. Additionally, it discusses properties, advantages, and real-world applications of zero knowledge proofs, highlighting their role in secure authentication and data integrity.module 4 ppt on crypography and network security
module 4 ppt on crypography and network securityPoornimaGn3
Ìę
The document discusses private-key and public-key cryptography, highlighting the differences between symmetric and asymmetric methods of securing communications. It explains the RSA algorithm for public-key cryptography, detailing key generation, encryption, and decryption processes, as well as the security aspects of RSA based on large integer factorization. Additionally, it introduces the Diffie-Hellman key exchange method for securely sharing keys between users.Quantum factorization.pdf
Quantum factorization.pdfssuser8b461f
Ìę
This document discusses methods for finding the period of a periodic function using discrete Fourier transforms (DFT). It presents two algorithms:
1. Algorithm I handles the special case where the period s divides the number of sample points N. It uses DFT to obtain frequencies that reveal the period.
2. Algorithm II handles the general case where s does not necessarily divide N. It uses continued fractions to approximate measured frequencies as rational numbers, whose denominators likely equal the period s.
The document also discusses applications to integer factorization by finding the period of functions over finite fields, and limitations of the classical approach that motivate the use of quantum computing.Rsa in CTF
Rsa in CTFSoL ymx
Ìę
This document summarizes various attacks on the RSA cryptosystem over 30 years, including:
- When p=q, the private key can be derived from the public key
- Using twin primes p and p+2 to factor the modulus
- Hastad's broadcast attack to derive the plaintext from encryptions using the same message but different public keys
- Wiener's attack and Boneh-Durfee's attack to derive the private key d when it is below a certain threshold based on the modulus n
- Common modulus attacks when encryptions use the same modulus n but different public exponents e
- Issues that can arise from reusing the prime factors p and q in different keysDigital Fingerprinting
Digital Fingerprintingsanthu652
Ìę
This document provides an overview of digital fingerprinting technology. It explains that digital fingerprinting can automatically identify phrases from confidential documents that appear in analyzed texts. The technology works by analyzing media like songs or videos to identify unique portions that can be matched to a database. Major companies like YouTube and Audible Magic use digital fingerprinting to identify copyrighted content and prevent unauthorized sharing. The document also discusses watermarking and how fingerprinting offers a more effective way to restrict copyrighted material than visible watermarks.Bch codes
Bch codesGaurav Thakur
Ìę
This document provides information about BCH codes, including:
1. BCH codes are linear cyclic block codes that can detect and correct errors. They allow flexibility in choosing block length and code rate.
2. Key characteristics of BCH codes include the block length being 2m - 1, error correction ability up to t errors where t<(2m - 1)/2, and minimum distance of at least 2t + 1.
3. Galois fields are finite fields that are important for constructing BCH codes. A generator polynomial is chosen based on the roots in the Galois field and is used to encode messages into codewords.implementing the encryption in the JAVA.ppt
implementing the encryption in the JAVA.pptMuhammadAbdullah311866
Ìę
The document describes how to implement RSA encryption in Java using the BigInteger class. It discusses:
1) Generating random prime numbers p and q using BigInteger's probablePrime method.
2) Computing n=p*q and Ï(n)=(p-1)*(q-1) to get the public modulus and Euler's totient function.
3) Finding a random integer k that is relatively prime to Ï(n) using gcd.
4) Computing the private exponent d as k's modular inverse modulo Ï(n) using modInverse.Introduction to Homomorphic Encryption
Introduction to Homomorphic Encryptionhubx
Ìę
The document explains homomorphic encryption, highlighting its ability to perform operations on encrypted data without decryption, which enhances privacy in various applications such as medical records and spam filtering. It discusses different types of homomorphisms and compares various encryption schemes, emphasizing the importance of selecting an appropriate scheme for specific applications. Practical examples illustrate how homomorphic encryption can facilitate secure computations while maintaining data privacy.Codes and Isogenies
Codes and IsogeniesPriyanka Aash
Ìę
The document summarizes a presentation on revocable identity-based encryption (RIBE) from codes with rank metric. Key points:
- RIBE adds an efficient revocation procedure to identity-based encryption by using a binary tree structure and key updates.
- The construction is based on low rank parity-check codes, with the master secret key defined as the "trapdoor" generated by the RankSign algorithm.
- Security relies on the rank syndrome decoding problem. Key updates are done efficiently through the binary tree with logarithmic complexity.
- Parameters are given that allow decoding of up to 2wr errors with small failure probability, suitable for the identity-based encryption scheme.Blockchain Technology - Week 6 - Role of Cryptography in Blockchain
Blockchain Technology - Week 6 - Role of Cryptography in BlockchainFerdin Joe John Joseph PhD
Ìę
The document discusses the role of cryptography in blockchain, focusing on hashing and the RSA algorithm. It explains key concepts, properties of hashing, and provides detailed examples of encryption and decryption using the RSA methodology, as well as the operation of secure hashing algorithms like SHA-1 and SHA-2. The session concludes with a mention of upcoming topics related to fraud and intrusion detection.Asymptotic Notation
Asymptotic Notationsohelranasweet
Ìę
This document discusses analyzing algorithms and asymptotic notation. It defines running time as the number of primitive operations before termination. Examples are provided to illustrate calculating running time functions and classifying them by order of growth such as constant, logarithmic, linear, quadratic, and exponential time. Asymptotic notation such as Big-O, Big-Omega, and Big-Theta are introduced to classify functions by their asymptotic growth rates. Examples are given to demonstrate determining tight asymptotic bounds between functions. Recurrences are defined as equations describing functions in terms of smaller inputs and base cases, which are useful for analyzing recurrent algorithms.Ad
Homomorphic Encryption
- 1. Homomorphic Encryption Craig Gentry scheme
- 2. Why homomorphic encryption? âą Proposed by Rivest, Adleman and Dertouzos âą Confidentiality problems âą Ability to compute over ciphertext instead of plaintext âą One could use information without knowing the content of that information âą Privacy garanteed
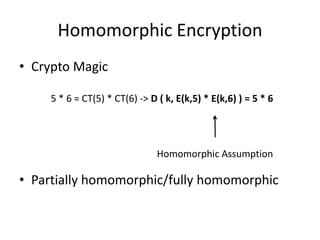
- 3. Homomorphic Encryption âą Crypto Magic 5 * 6 = CT(5) * CT(6) -> D ( k, E(k,5) * E(k,6) ) = 5 * 6 Homomorphic Assumption âą Partially homomorphic/fully homomorphic
- 4. Homomorphic Encryption âą Partially homomorphic schemes â RSA: CT(x)*CT(y) = (xe mod M) * (ye mod M) = xeye mod M = (xy)e mod M = CT(x*y), where e is the exponent key and M the modulus âą p=61; âą q=53; âą N=3233; ⹠Ί(N)=60*52=3120; âą e=17; âą d=2753;
- 5. Homomorphic Encryption âą Partially homomorphic schemes â RSA: Obtain 5*6 performing RSA(5)*RSA(6) âą RSA(5) = 517 (mod 3233) = 3086; âą RSA(6) = 617 (mod 3233) = 824; âą 3068*824 = 2542864; âą RSA-1(2542864) = 25428642753 (mod 3233) = 30; âą 5*6 = 30;
- 6. Homomorphic Encryption âą Fully homomorphic schemes â Craig Gentry scheme âą Based on ideal lattices â Zaryab Khan scheme âą Based on perfectly colorblind function
- 7. Craig Gentry scheme âą Suppose a scheme with a ânoise parameterâ attached to each CT; âą Encryption algorithm outputs a CT with a small noise parameter (say less than n); âą Decryption algorithm only works if noise is less than some parameter N >> n; âą To compute E(a+b) / E(a*b), include noise; âą This gives a âsomewhat homomorphicâ scheme.
- 8. Craig Gentry scheme âą Now suppose a new algorithm RECRYPT, such that: â Input: E(a), with noise Nâ < N â Output: Eâ(a), with noise âN âą âSomewhat homomorphicâ -> fully homomorphic! âą Apply RECRYPT to E(a) and E(b) to ensure that the noise in E(a*b) or E(a+b) is smaller than N âą âBootstrappableâ
- 9. Craig Gentry scheme (integers) âą Key: odd integer p > 2N âą Encryption algorithm: given a bit b -> E(b) = c = b + 2x + kp, where x is in [-n/2,n/2] and k is an integer chosen from some range âą Decryption algorithm: b = (c mod p) mod 2, where (c mod p) is the noise and belongs to [-n,n] âą Decryption works if b + 2x â [-N,N] â[-p/2,p/2]
- 10. Craig Gentry scheme (integers) âą Graig Gentry schemeâs homomorphic assumptions â Addiction: c1 + c2 = b1+ b2 + 2(x1+x2) + (k1+k2)p = b1 xor b2 + 2x + kp âą Decryption works if (b1+2x1) + (b2+2x2) is in [- N,N] â Multiplication: c1*c2 = b1*b2 + 2(b1x2 + b2x1 + 2x1x2) + kp = b1*b2 + 2x + kp âą Decryption works if (b1+2x1) * (b2+2x2) is in [- N,N]
- 11. Craig Gentry scheme (integers) âą Addition example: 4+4 â CT(100): 22 21 21 âą CT(1) = 1 + 2*3 + 5*3 = 22 +22 21 21 âą CT(0) = 0 + 2*3 + 5*3 = 21 44 42 42 âą CT(0) = 0 + 2*3 + 5*3 = 21 â D(44 42 42): âą D(44) = 44 mod 3 = 2 âą D(42) = 42 mod 3 = 0 1000 = 8 = 4+4 âą D(42) = 42 mod 3 = 0
- 12. Craig Gentry scheme (integers) âą Multiplication example: 4*4 â CT(100): âą CT(1) = 1 + 2*3 + 5*3 = 22 22 21 21 âą CT(0) = 0 + 2*3 + 5*3 = 21 Ă22 21 21 âą CT(0) = 0 + 2*3 + 5*3 = 21 484 924 1365 882 441 â D(484 924 1365 882 441): âą D(484) = 484 mod 3 = 1 âą D(924) = 924 mod 3 = 0 âą D(1365) = 1365 mod 3 = 0 10000 = 16 = 4*4 âą D(882) = 882 mod 3 = 0 âą D(441) = 441 mod 3 = 0
- 13. Craig Gentry scheme (ideal lattices) âą Replace integers by ideal lattices âą Ideal lattices have many representations or âbasesâ âą Bases: â Good: good to decrypt, bad to encrypt â Bad: bad to decrypt, good to encrypt âą Public key scheme, where good bases are private keys and bad bases are public keys
- 14. Cryptography over lattices âą L = ζ(B) = {Bc : c â Zk}, B â RnĂk, where the k columns of the basis are linearly independent âą NP-hard problems over lattices: â SVP (shortest vector problem): given a basis for lattice L of size n, find the shortest nonzero vector v â L s.t. ||v|| = λ(L); â CVP (closest vector problem): given a basis for lattice L of size n and a vector t â Rn, find a nonzero vector v â L s.t. ||t-v|| †γ;
- 15. Cryptography over lattices âą NP-hard problems over lattices: â SIVP (shortest independent vector problem): like the SVP, except the output are linearly independent vectors v1, âŠ, v2 â L of length at most λ(L); â BDDP (bounded distance decoding problem): same as CVP but with the promise that there is a unique solution.
- 16. Craig Gentry scheme âą Why inefficient? â CT size and computation time increase sharply as the security level increases; â 2k security -> CT size and computation time are high-degree polynomials in k; â Efforts are being made to reduce the computational requirements of Craig Gentry construction
- 17. Homomorphic Encryption âą Nowadays: â Craig Gentry presented a working implementation of the fully homomorphic system, including the bootstrapping function â Exists a practical application of homomorphic encryption to a hybrid wireless network â Perform statistical tests over encrypted data such as temperature, humidity, etc. â There are also some practical implementations of simplifications of this scheme over databases
- 18. Problems solved âą Cloud security âą Problems related to personal records like medical records âą Work with information stored in databases âą Querys to search engines âą âŠ
- 19. My Project âą Design an API and include it on a Web Service that will work over CLOUD platforms âą The API should provide homomorphic encryption functions to be used âą Create a prototype that will work under the constructed API
- 20. QUESTIONS?
