�ݺ�ߣ

Performing Hypothesis Tests
Dr. Monica Brussolo

Chapter 9: Hypothesis Testing
• Population Mean: 𝜎 Known
• Population Mean: 𝜎 Unknown

Method 1: p-value
One-tailed hypothesis test
• The p-value is the probability, computed using the test statistic, that
measures the support (or lack of support) provided by the sample
for the null hypothesis.
• If the p-value is less than or equal to the level of significance , we
reject the null hypothesis.
• Reject H0 if the p-value < 
3

Suggested Guidelines for Interpreting
p-values
• Interpreting the p-value when we are not give an α-value
11-4

Method 2: Critical Value
One-tailed hypothesis test
5
• We can use the standard normal probability distribution table to find the 𝑧 −
𝑣𝑎𝑙𝑢𝑒 with an area of 𝛼 in the lower (or upper) tail of the distribution.
• The value of the test statistic that established the boundary of the rejection
region is called the critical value for the test. The rejection rule is:
• Lower Tail: Reject 𝐻0 if 𝑧 ≤ −𝑧𝛼
• Upper Tail: Reject 𝐻0 if 𝑧 ≥ 𝑧𝛼

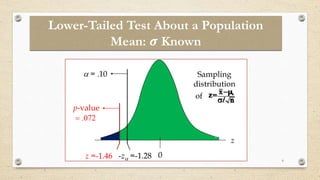
6
Lower-Tailed Test About a Population
Mean: 𝝈 Known
p-value
72
0
-z =-1.28
 = .10
z
z =-1.46
Sampling
distribution
of n
/
x
z 0





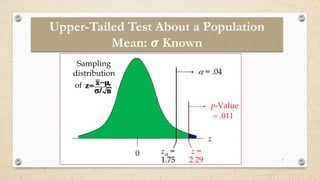
7
Upper-Tailed Test About a Population
Mean: 𝝈 Known
p-Value
11
0 z =
1.75
 = .04
z
z =
2.29
Sampling
distribution
of
n
/
x
z 0





Steps of Hypothesis Testing
8
1. Develop the null and alternative hypotheses.
2. Specify the level of significance 𝛼.
3. Collect the sample data and compute the value of the test statistic.
Method 1: 𝑝-value
4. Use the value of the test statistic to compute the 𝑝-value.
5. Reject 𝐻0 if the 𝑝 − 𝑣𝑎𝑙𝑢𝑒 < 𝛼

Steps of Hypothesis Testing
9
4. Use the level of significance to determine the critical value and the
rejection rule.
5. Use the value of the test statistic and the rejection rule to determine
whether to reject 𝐻0.

Example: Metro EMS
One-Tailed Tests About a Population Mean: 𝝈 Known
10
The response times for a random sample of 40 medical
emergencies were tabulated. The sample mean is 13.25 minutes.
The population standard deviation is believed to be 3.2 minutes.
The EMS director wants to perform a hypothesis test, with a .05
level of significance, to determine whether the service goal of 12
minutes or less is being achieved.

Example: Metro EMS
11
Both Methods:
1. Develop the hypotheses.
2. Specify the level of significance 𝛼.
3. Compute the value of the test statistic.

12
4. Compute the 𝑝-value. For z =
cumulative probability = p–value =
5. Determine whether to Reject 𝐻0
Because p–value =  = .05
There is sufficient statistical evidence to infer that Metro EMS_____
meeting the response goal of 12 minutes.
Example: Metro EMS

13
4. Determine the critical value and the rejection rule. For  = .05, z.05 =
Reject H0 if z >
There is sufficient statistical evidence to infer that Metro EMS_____
meeting the response goal of 12 minutes.
Example: Metro EMS

Method 1: p-Value
Two-Tailed Hypothesis Testing
14
Compute the 𝑝-value using the following three steps:
1. Compute the value of the test statistic 𝑧.
2. If 𝑧 is in the upper tail (𝑧 > 0), find the area under the standard normal
curve to the right of 𝑧.
If 𝑧 is in the lower tail (𝑧 < 0), find the area under the standard normal
curve to the left of 𝑧.
3. Double the tail area obtained in step 2 to obtain the 𝑝 –value.
Rejection rule: Reject 𝐻0 if the 𝑝 − 𝑣𝑎𝑙𝑢𝑒 ≤ 𝛼

Two-Tailed Hypothesis Testing
15
1. The critical values will occur in both the lower and upper tails of the
standard normal curve.
2. Use the standard normal probability distribution table to find 𝑧𝛼/2
(the 𝑧-value with an area of 𝛼/2 in the upper tail of the
distribution).
Rejection rule: Reject 𝐻0 if 𝑧 ≤ −𝑧𝛼/2 or 𝑧 ≥ 𝑧𝛼/2

Example: Glow Toothpaste
Two-Tailed Tests About a Population Mean: 𝝈 Known
16
The production line for Glow toothpaste is designed to fill tubes with a mean
weight of 6 𝑜𝑧. Periodically, a sample of 30 tubes will be selected in order to
check the filling process.
Quality assurance procedures call for the continuation of the filling process if
the sample results are consistent with the assumption that the mean filling
weight for the population of toothpaste tubes is 6 𝑜𝑧.; otherwise the process
will be adjusted.

17
Assume that a sample of 30 toothpaste tubes provides a sample mean of
6.1 𝑜𝑧. The population standard deviation is believed to be 0.2 𝑜𝑧.
Perform a hypothesis test, at the .03 level of significance, to help determine
whether the filling process should continue operating or be stopped and
corrected.

18
Both Methods:
1. Determine the hypotheses.
2. Specify the level of significance.

19
4. Compute the 𝑝-value.
There is sufficient statistical evidence to infer that the alternative
hypothesis is _____________(i.e. the mean filling weight _______6
ounces).

20
4. Determine the critical value and the rejection rule.
There is sufficient statistical evidence to infer that the alternative
hypothesis is ________
(i.e. the mean filling weight _______6 ounces).

21
/2 =
.015
0
z/2 = 2.17
z
/2 =
.015
-z/2 = -2.17
z = 2.74
z = -2.74
1/2
p -value
= .0031
1/2
p -value
= .0031
Do Not Reject H0

Tests About a Population Mean:
𝝈 Unknown
22
 Test Statistic
𝑡 =
𝑥 − 𝜇0
𝑠/ 𝑛
This test statistic has a 𝑡 distribution with 𝑛 − 1 degrees of
freedom.

Tests About a Population Mean:
𝝈 Unknown
23
 Rejection Rule: Critical Value Approach
 𝐻0: 𝜇 ≥ 𝜇0 Reject 𝐻0 if 𝑡 ≤ −𝑡𝛼 (lower tail)
 𝐻0: 𝜇 ≤ 𝜇0 Reject 𝐻0 if 𝑡 ≥ 𝑡𝛼 (upper tail)
 𝐻0: 𝜇 = 𝜇0 Reject 𝐻0 if 𝑡 ≤ −𝑡𝛼/2 or 𝑡 ≥ 𝑡𝛼/2

Example: Highway Patrol
One-Tailed Tests About a Population Mean: 𝝈 Unknown
24
A State Highway Patrol periodically samples vehicle speeds at various
locations on a particular roadway. The sample of vehicle speeds is used to
test the hypothesis 𝐻0: 𝜇 ≤ 65.
The locations where 𝐻0 is rejected are deemed the best locations for radar
traps. At Location F, a sample of 64 vehicles shows a mean speed of
66.2 𝑚𝑝ℎ with a standard deviation of 4.2 𝑚𝑝ℎ. Use α = .05 to test the
hypothesis.

25
METHOD: Critical Value (the only method discussed for t-test)
1. Determine the hypotheses.
2. Specify the level of significance.

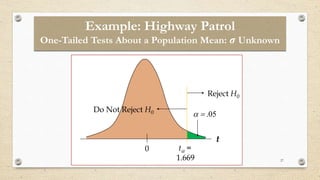
26
Method: Critical Value
4. Determine the critical value and the rejection rule.
For  = and d.f. = t.05 = Reject H0 if t >
Because > we reject H0.
We __________95% confident that the mean speed of vehicles at Location
F__________ than 65 mph. Location F is a good candidate for a radar trap.

27

0 t =
1.669
Reject H0
Do Not Reject H0
t

�ݺ�ߣ

Hypothesis

More Related Content

Similar to Hypothesis (20)

Recently uploaded (20)

Hypothesis