ICCV2019読み会「Learning Meshes for Dense Visual SLAM」
- 1. ICCV2019読み会 「Learning Meshes for Dense Visual SLAM」 2019.10.19 kagami
- 2. 論?について ? 著者: Andrew J. Davisonのグループ ?DTAM, CodeSLAM, SceneCode ? 主張: Visual SLAMに対して、 コンパクトで密な三次元表現 である三?メッシュを導? 2
- 3. Visual SLAM ? geometry representation 3 Sparse (PTAM, ORB-SLAM2, …) Dense / Semi-dense (DTAM, LSD-SLAM, …) ? : 計算コストが低い ? : 密度が低い ? : 密度が?い ? : 計算コストが?い → Denseな三次元復元をしたいが、計算コストがネック…
- 4. Previous work: CodeSLAM[M.Bloesch+, CVPR18] ? Depth情報をコンパクトに表現する特徴量”code”の導? ? Decoder(?(?))をlinearにすることでJacobianを事前に計 算できる 4 参考 (CodeSLAMの紹介スライド) /MasayaKaneko/codeslam https://docs.google.com/presentation/d/1GrFIy24_b9zrh11Z-Bzz25f1T3XTk0Y- y6A_nsiiqGE/edit#slide=id.g3b0d7b12ed_0_70 depthcode ? ?(?) ?
- 5. This work ? Mesh(2.5D triangular mesh)によるコンパクトなdepth表現 を導? 5 depthmesh ? ?(?) ? → CodeSLAMのようにJacobianを事前に計算できるようなパラメータ表現にしたい
- 6. Mesh representation ? meshの各頂点 ? ?(3DoF)を以下のように表現 ?カメラ平?上の座標 ? ? (2DoF) l DNNによって推定され、最適化時は固定 ?Inverse depth ?( (1DoF) l 最適化により推定 ? inverse depthをdepth表現で使?する理由 1. Inverse depthの不確かさの分布がガウス分布に近い 2. Meshの各頂点のinverse depthから全体のinverse depthの 線形変換が可能 6 mesh全体のinverse depth ? ? は最適化時固定 のため、 ?(?) は最適化時不変のため、事前に計算可能 ? CodeSLAMに?べてsparse なため、計算負荷軽減 Mesh頂点のinverse depth
- 7. Meshのカメラ平?上の座標を推定 ? 画像からDNNでmeshの頂点 ? を推定 1. 規則的にmeshの頂点を配置 2. U-Netによるpixel-wiseの特徴量抽出 3. U-Netの最終layerからmeshの頂点周りのパッチを抽出し、 全結合層を通して、頂点の移動量を算出 7 画像 U-Net 特徴量 全結合層 meshの各頂点座標
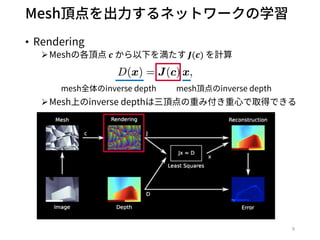
- 9. Mesh頂点を出?するネットワークの学習 ? Rendering ?Meshの各頂点 ? から以下を満たす ?(?) を計算 ?Mesh上のinverse depthは三頂点の重み付き重?で取得できる 9 mesh全体のinverse depth mesh頂点のinverse depth
- 10. Mesh頂点を出?するネットワークの学習 ? Least Square ?Meshの各頂点のinverse depth ? と全体のinverse depth map ?(?) は線形変換 → 最??乗で解ける ?求めた ? をもとに全体のinverse depth mapを得られる 10
- 11. Mesh頂点を出?するネットワークの学習 ? Reconstruction error ?真値とのinverse depth mapの差をロスとする ?式変形により、メッシュの頂点座標 ? の関数として表現できる ?三次元構造を表現するのに適切なmeshの座標を取得できる! 11
- 12. 次はinverse depthの推定 ? カメラポーズとgeometryを同時に推定したい → CodeSLAMのようにkey-frameベースの最適化 ? 以下のようなfactor graphで定式化 12 変数 ?.: カメラポーズ ?.: inverse depth factor ?.: prior factor factor ?.1: stereo factor → この定式化により、他のセンサ情報(IMUなど)を追加したい場合、factorを追加 するだけなので、拡張性が?い ?2,4 … … … ?4,5 ?674,6 ?2 ?4 ?5 ?6 ?2, ?2 ?4, ?4 ?5, ?5 ?6, ?6
- 13. 次はinverse depthの推定 ? 2つのfactorを?いてカメラポーズとinverse depthを 同時に最適化 ?最適化は学習ベースではなく、Gauss-Newton法を?いる 13 変数 ?.: カメラポーズ ?.: inverse depth factor ?.: prior factor factor ?.1: stereo factor ?2,4 … … … ?4,5 ?674,6 ?2 ?4 ?5 ?6 ?2, ?2 ?4, ?4 ?5, ?5 ?6, ?6 Data-driven learnable factor ? 画像から得られる先?情報による拘束 Geometry-aware learnable factor ? 同じシーンの観測に対する拘束
- 14. Prior factor ? Prior factor ?(?.): 画像 ?. から得られるgeometryの先 ?情報 ?Smoothnessの制約 ?Meshの曲率を抑える ? meshの座標 ? の取得と同じアプローチ 1. U-Netによるpixel-wiseの特徴量抽出 2. U-Netの最終layerからmeshの頂点周りのパッチを抽出 3. パッチからprior factorを計算 14画像 U-Net 特徴量 ?(?)
- 15. Prior factor ? パッチから三種類のpriorを計算 1. 1つのパッチのみによるprior 各頂点のdepth情報 2. 三?メッシュを形成する3つのパッチによるprior 三?メッシュなどの?度情報 3. 隣接する?つの三?メッシュの4つのパッチによるprior Smoothness制約につながる情報 ? 1,2,3をまとめて以下のようにinverse depthに対して 線形なpriorを得られる 15
- 16. Stereo factor ? Stereo factor ?.1(?., ?1, ?., ?1) : keyframe間で同じシー ンの観測に対する拘束 ? 画像 ?., ?1 から対応する位置の何かしらの残差を計算し たい 16 Reprojection error ? 対応点における再投影誤差 Photometric error ? 再投影された画素の輝度値の差 ? : ロバスト性が?い ? : 対応点の計算が必要 ? : 対応点の計算が不要 ? : ロバスト性が低い
- 17. Feature-metric error ? 再投影されたFeature(?)の誤差を最?化 ?Proposed by BA-Net[C.Tang+, ICLR19] ? 特徴 ?照明変化に対するロバスト性が?い特徴量の獲得 ?凸性の?い特徴量の獲得 17 参考 (BA-Netの紹介スライド) /MaiNishimura2/banet-dense-bundle-adjustment-network-3d
- 18. Stereo factor ? 特徴量空間における残差を最?化 ? 特徴量?はMeshのカメラ平?上の座標を出?するネッ トワークと同じアーキテクチャ(最終層のチャンネルの み3に変更) 18 特徴量の各次元における残差 重み
- 19. ネットワークの学習 ? Gauss-Newtonによる最適化における残差を学習 ? 計算コストにより、学習時は2フレームのみを使?し、 Gauss-Newtonは3ステップ ? 最適化中は学習パラメータは固定。最適化後の誤差を もとに逆伝搬 19
- 20. Gauss-Newton 法 ? Objective: コスト関数を最?にする?を求めたい ? Algorithm 1. 適当な初期値?を設定 2. コスト関数?(?)のヤコビアン?(?)を計算 3. 以下の式を解いて??を計算 4. ? → ? + ??に更新 20
- 21. Previous work: LS-Net ? LS-Net: Learning to Solve Nonlinear Least Squares for Monocular Stereo [R.Clark+, ECCV18] ?NNがパラメータの更新を出? ? デメリット ?フレーム数やiteration回数が固定 ?他のセンサ情報の統合などの柔軟性が低い 21 OptimizerをNN化
- 22. ネットワークの学習 ? コスト関数 ? Gauss-Newtonで?を最適化後、最終的なコストを逆伝 搬し、パラメータ?, ?, ?, ?を更新 22 prior factor stereo factor
- 23. Datasets ? SceneNet RGB-D(SN) [J.McCormac+, ICCV17] ?Synthetic dataset ? TUM’s RGB-D SLAM dataset (TM) [J.Sturm+, IROS12] ?Real data 23
- 24. Results: 2D mesh ? Meshのカメラ平?上の座標の推定結果 ?Depthの不連続な位置や曲率の?い領域に集中 ??い領域(low activation)に集中 24 Image feature activation 2D mesh
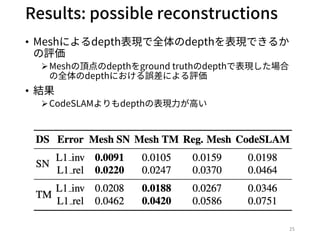
- 25. Results: possible reconstructions ? Meshによるdepth表現で全体のdepthを表現できるか の評価 ?Meshの頂点のdepthをground truthのdepthで表現した場合 の全体のdepthにおける誤差による評価 ? 結果 ?CodeSLAMよりもdepthの表現?が?い 25
- 26. Results: possible reconstructions ? ground truthに対して最適化した結果と学習された priorのみでの推定結果 ? Priorのみの結果を初期値として使えそう 26 Image GT depth Mesh w/ prior CodeSLAM w/ prior CodeSLAM optim. GT Mesh optim. GT
- 27. Results: learned prior ? 学習されたpriorによる推定結果 27 u AS: auto-scaled(scaleのoffsetを調整) u CodeSLAM: zero code prediction
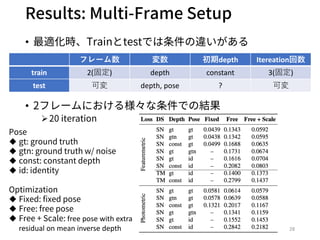
- 28. Results: Multi-Frame Setup ? 最適化時、Trainとtestでは条件の違いがある ? 2フレームにおける様々な条件での結果 ?20 iteration 28 フレーム数 変数 初期depth Itereation回数 train 2(固定) depth constant 3(固定) test 可変 depth, pose ? 可変 Pose u gt: ground truth u gtn: ground truth w/ noise u const: constant depth u id: identity Optimization u Fixed: fixed pose u Free: free pose u Free + Scale: free pose with extra residual on mean inverse depth
- 29. Results: Multi-Frame Setup ? 最適化に使?するフレーム数を変化させた時の結果 ?フレーム数が増えるほど精度が?くなる 29
- 31. まとめ ? Contribution ?三?メッシュを?いて、カメラポーズとgeometryの同時推定を可 能にした ?メッシュの表現の仕?(2つに分割)がポイント l カメラ平?上の座標: DNNによって推定 l Inverse depth: 最適化によって推定 ?Factor graphによる拡張性の?い定式化 l Prior factor: data-drivenな先?情報 l Stereo factor: geometry-awareな拘束 ? Future work ?Datasetによる依存が?きいため、self-supervised lossの導? ?本格的なSLAMシステムへの拡張 l Incremental, refinement 31


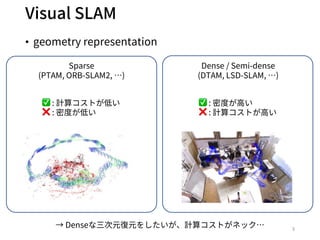
![Previous work: CodeSLAM[M.Bloesch+, CVPR18]
? Depth情報をコンパクトに表現する特徴量”code”の導?
? Decoder(?(?))をlinearにすることでJacobianを事前に計
算できる
4
参考 (CodeSLAMの紹介スライド)
/MasayaKaneko/codeslam
https://docs.google.com/presentation/d/1GrFIy24_b9zrh11Z-Bzz25f1T3XTk0Y-
y6A_nsiiqGE/edit#slide=id.g3b0d7b12ed_0_70
depthcode
?
?(?)
?](https://image.slidesharecdn.com/learningmesh-191019031240/85/ICCV2019-Learning-Meshes-for-Dense-Visual-SLAM-4-320.jpg)











![Feature-metric error
? 再投影されたFeature(?)の誤差を最?化
?Proposed by BA-Net[C.Tang+, ICLR19]
? 特徴
?照明変化に対するロバスト性が?い特徴量の獲得
?凸性の?い特徴量の獲得
17
参考 (BA-Netの紹介スライド)
/MaiNishimura2/banet-dense-bundle-adjustment-network-3d](https://image.slidesharecdn.com/learningmesh-191019031240/85/ICCV2019-Learning-Meshes-for-Dense-Visual-SLAM-17-320.jpg)



![Previous work: LS-Net
? LS-Net: Learning to Solve Nonlinear Least Squares
for Monocular Stereo [R.Clark+, ECCV18]
?NNがパラメータの更新を出?
? デメリット
?フレーム数やiteration回数が固定
?他のセンサ情報の統合などの柔軟性が低い
21
OptimizerをNN化](https://image.slidesharecdn.com/learningmesh-191019031240/85/ICCV2019-Learning-Meshes-for-Dense-Visual-SLAM-21-320.jpg)

![Datasets
? SceneNet RGB-D(SN) [J.McCormac+, ICCV17]
?Synthetic dataset
? TUM’s RGB-D SLAM dataset (TM) [J.Sturm+, IROS12]
?Real data
23](https://image.slidesharecdn.com/learningmesh-191019031240/85/ICCV2019-Learning-Meshes-for-Dense-Visual-SLAM-23-320.jpg)