�ݺ�ߣ

Quantum conditional states, Bayes’ rule, and
state compatibility

M. S. Leifer (UCL)
Joint work with R. W. Spekkens (Perimeter)

Imperial College QI Seminar
14th December 2010

Outline

1 Quantum conditional states

2 Hybrid quantum-classical systems

3 Quantum Bayes’ rule

4 Quantum state compatibility

5 Further results and open questions

Topic

1 Quantum conditional states

2 Hybrid quantum-classical systems

3 Quantum Bayes’ rule

4 Quantum state compatibility

5 Further results and open questions

Classical vs. quantum Probability

Table: Basic deﬁnitions

Classical Probability Quantum Theory

Sample space Hilbert space
ΩX = {1, 2, . . . , dX } HA = CdA
= span (|1 , |2 , . . . , |dA )

Probability distribution Quantum state
P(X = x) ≥ 0 ρA ∈ L+ (HA )
x∈ΩX P(X = x) = 1 TrA (ρA ) = 1

Classical vs. quantum Probability

Table: Composite systems

Classical Probability Quantum Theory

Cartesian product Tensor product
ΩXY = ΩX × ΩY HAB = HA ⊗ HB

Joint distribution Bipartite state
P(X , Y ) ρAB

Marginal distribution Reduced state
P(Y ) = x∈ΩX P(X = x, Y ) ρB = TrA (ρAB )

Conditional distribution Conditional state
P(Y |X ) = P(X ,Y )
P(X ) ρB|A =?

Definition of QCS

Definition
A quantum conditional state of B given A is a positive operator
ρB|A on HAB = HA ⊗ HB that satisfies

TrB ρB|A = IA .

c.f. P(Y |X ) is a positive function on ΩXY = ΩX × ΩY that
satisfies
P(Y = y |X ) = 1.
y ∈ΩY

Relation to reduced and joint States

√ √
(ρA , ρB|A ) → ρAB = ρA ⊗ IB ρB|A ρA ⊗ IB

ρAB → ρA = TrB (ρAB )

ρB|A = ρ−1 ⊗ IB ρAB
A ρ−1 ⊗ IB
A


√ √


A ρ−1 ⊗ IB
A

Note: ρB|A deﬁned from ρAB is a QCS on supp(ρA ) ⊗ HB .


√ √


A ρ−1 ⊗ IB
A


P(X ,Y )
c.f. P(X , Y ) = P(Y |X )P(X ) and P(Y |X ) = P(X )

Notation

• Drop implied identity operators, e.g.

• IA ⊗ MBC NAB ⊗ IC → MBC NAB

• MA ⊗ IB = NAB → MA = NAB

• Deﬁne non-associative “product”

√ √
• M N= NM N

Classical conditional probabilities

Example (classical conditional probabilities)
Given a classical variable X , deﬁne a Hilbert space HX with a
preferred basis {|1 X , |2 X , . . . , |dX X } labeled by elements of
ΩX . Then,
ρX = P(X = x) |x x|X
x∈ΩX

Similarly,

ρXY = P(X = x, Y = y ) |xy xy |XY
x∈ΩX ,y ∈ΩY

ρY |X = P(Y = y |X = x) |xy xy |XY
x∈ΩX ,y ∈ΩY

Correlations between subsystems

X Y A B

Figure: Classical correlations Figure: Quantum correlations

ρAB = ρB|A ρA
P(X , Y ) = P(Y |X )P(X )

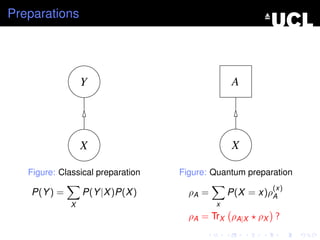
Preparations

Y A

X X

Figure: Classical preparation Figure: Quantum preparation
(x)
P(Y ) = P(Y |X )P(X ) ρA = P(X = x)ρA
X x
ρA = TrX ρA|X ρX ?

What is a Hybrid System?

• Composite of a quantum system and a classical random
variable.

• Classical r.v. X has Hilbert space HX with preferred basis
{|1 X , |2 X , . . . , |dX X }.

• Quantum system A has Hilbert space HA .

• Hybrid system has Hilbert space HXA = HX ⊗ HA

What is a Hybrid System?

• Composite of a quantum system and a classical random
variable.

• Classical r.v. X has Hilbert space HX with preferred basis
{|1 X , |2 X , . . . , |dX X }.

• Quantum system A has Hilbert space HA .

• Hybrid system has Hilbert space HXA = HX ⊗ HA

• Operators on HXA restricted to be of the form

MXA = |x x|X ⊗ MX =x,A
x∈ΩX



x∈ΩX

Proposition
on HA

• Ensemble decomposition: ρA = x P(X = x)ρA|X =x



x∈ΩX

Proposition
on HA

• Ensemble decomposition: ρA = TrX ρX ρA|X



x∈ΩX

Proposition
on HA

√ √
• Ensemble decomposition: ρA = TrX ρX ρA|X ρX


x∈ΩX

Proposition
on HA

• Ensemble decomposition: ρA = TrX ρA|X ρX


x∈ΩX

Proposition
on HA

• Ensemble decomposition: ρA = TrX ρA|X ρX

• Hybrid joint state: ρXA = x∈ΩX P(X = x) |x x|X ⊗ ρA|X =x

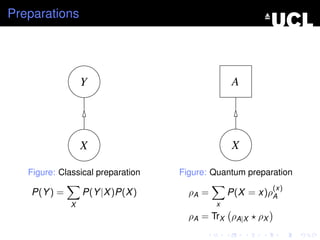
Preparations

Y A

X X

Figure: Classical preparation Figure: Quantum preparation
(x)
P(Y ) = P(Y |X )P(X ) ρA = P(X = x)ρA
X x
ρA = TrX ρA|X ρX

Measurements

Y Y

X A

Figure: Noisy measurement Figure: POVM measurement
(y )
P(Y ) = P(Y |X )P(X ) P(Y = y ) = TrA EA ρA
X
ρY = TrA ρY |A ρA ?



ρY |A = |y y |Y ⊗ ρY =y |A
y ∈ΩY

Proposition

• Generalized Born rule: P(Y = y ) = TrA ρY =y |A ρA



ρY |A = |y y |Y ⊗ ρY =y |A
y ∈ΩY

Proposition

• Generalized Born rule: ρY = TrA ρY |A ρA



ρY |A = |y y |Y ⊗ ρY =y |A
y ∈ΩY

Proposition

√ √
• Generalized Born rule: ρY = TrA ρA ρY |A ρA



ρY |A = |y y |Y ⊗ ρY =y |A
y ∈ΩY

Proposition

• Generalized Born rule: ρY = TrA ρY |A ρA

√ √
• Hybrid joint state: ρYA = y ∈ΩY |y y |Y ⊗ ρA ρY =y |A ρA

State update rules

• Classically, upon learning X = x:

P(Y ) → P(Y |X = x)

• Quantumly: ρA → ρA|X =x ?

State update rules

• Classically, upon learning X = x:

P(Y ) → P(Y |X = x)

• Quantumly: ρA → ρA|X =x ?

• When you don’t know the value of X
A state of A is:

ρA = TrX ρA|X ρX
= P(X = x)ρA|X =x
X x∈ΩX

Figure: Preparation • On learning X=x: ρA → ρA|X =x

State update rules

• Classically, upon learning Y = y :

P(X ) → P(X |Y = y )

• Quantumly: ρA → ρA|Y =y ?

Y • When you don’t know the value of Y
state of A is:

ρA = TrY ρY |A ρA

A
• On learning Y=y: ρA → ρA|Y =y ?
Figure: Measurement

Aside: Quantum conditional independence

• General tripartite state on HABC = HA ⊗ HB ⊗ HC :

ρABC = ρC|AB ρB|A ρA




Deﬁnition
If ρC|AB = ρC|B then C is conditionally independent of A given B.




Deﬁnition

Theorem
ρC|AB = ρC|B iff ρA|BC = ρA|B

Summary of state update rules

Table: Which states update via Bayesian conditioning?

Updating on: Predictive state Retrodictive state

Preparation X
variable

Direct
measurement X
outcome

Remote
measurement It’s complicated
outcome

Introduction to State Compatibility

(A) (B)
ρS ρS

S

Alice Bob
Figure: Quantum state compatibility

• Alice and Bob assign different states to S
• e.g. BB84: Alice prepares one of |0 S , |1 S , |+ S , |− S
I
• Bob assigns dS before measuring
S

(A) (B)
• When do ρS , ρS represent validly differing views?

Brun-Finklestein-Mermin Compatibility

• Brun, Finklestein & Mermin, Phys. Rev. A 65:032315
(2002).

Deﬁnition (BFM Compatibility)
(A) (B)
Two states ρS and ρS are BFM compatible if ∃ ensemble
decompositions of the form
(A) (A)
ρS = pτS + (1 − p)σS
(B) (B)
ρS = qτS + (1 − q)σS


(2002).

(A) (B)
(A)
ρS = pτS + junk
(B)
ρS = qτS + junk


(2002).

(A) (B)
(A)
ρS = pτS + junk
(B)
ρS = qτS + junk

• Special case:
• If both assign pure states then they must agree.

Objective vs. Subjective Approaches

• Objective: States represent knowledge or information.
• If Alice and Bob disagree it is because they have access to
different data.
• BFM & Jacobs (QIP 1:73 (2002)) provide objective
justiﬁcations of BFM.


different data.

• Subjective: States represent degrees of belief.
• There can be no unilateral requirement for states to be
compatible.
• Caves, Fuchs & Shack Phys. Rev. A 66:062111 (2002).


different data.

• Subjective: States represent degrees of belief.
• There can be no unilateral requirement for states to be
compatible.
• Caves, Fuchs & Shack Phys. Rev. A 66:062111 (2002).

• However, we are still interested in whether Alice and Bob
can reach intersubjective agreement.

Subjective Bayesian Compatibility

(A) (B)
ρS ρS

S

Alice Bob
Figure: Quantum compatibility

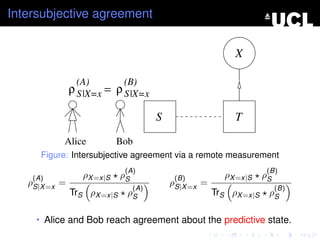
Intersubjective agreement

X

(A) (B)
ρS = ρS

S T

Alice Bob
Figure: Intersubjective agreement via a remote measurement

• Alice and Bob agree on the model for X

(A) (B)
ρX |S = ρX |S = ρX |S , ρX |S = TrT ρX |T ρT |S


(A) (B) S

Alice Bob X

Figure: Intersubjective agreement via a preparation vairable

• Alice and Bob reach agreement about the predictive state.


(A) (B) X

Alice Bob S

Figure: Intersubjective agreement via a measurement

• Alice and Bob reach agreement about the retrodictive
state.

Subjective Bayesian compatibility

Deﬁnition (Quantum compatibility)
(A) (B)
Two states ρS , ρS are compatible iff ∃ a hybrid conditional
state ρX |S for a r.v. X such that

(A) (B)
ρS|X =x = ρS|X =x

for some value x of X , where
(A) (A) (B) (B)
ρXS = ρX |S ρS ρX |S = ρX |S ρS

Theorem
(A) (B)
ρS and ρS are compatible iff they satisfy the BFM condition.

Subjective Bayesian justiﬁcation of BFM
BFM ⇒ subjective compatibility.
• Common state can always be chosen to be pure |ψ S

(A) (B)
ρS = p |ψ ψ|S + junk, ρS = q |ψ ψ|S + junk

• Choose X to be a bit with

ρX |S = |0 0|X ⊗ |ψ ψ|S + |1 1|X ⊗ IS − |ψ ψ|S .

• Compute

(A) (B)
ρS|X =0 = ρS|X =0 = |ψ ψ|S

Further results
Forthcoming paper(s) with R. W. Spekkens also include:
• Dynamics (CPT maps, instruments)
• Temporal joint states
• Quantum conditional independence
• Quantum sufﬁcient statistics
• Quantum state pooling

Earlier papers with related ideas:
• M. Asorey et. al., Open.Syst.Info.Dyn. 12:319–329 (2006).
• M. S. Leifer, Phys. Rev. A 74:042310 (2006).
• M. S. Leifer, AIP Conference Proceedings 889:172–186
(2007).
• M. S. Leifer & D. Poulin, Ann. Phys. 323:1899 (2008).

Open question

What is the meaning of fully quantum Bayesian
conditioning?

−1
ρB → ρB|A = ρA|B TrB ρA|B ρB ⊗ ρB

Thanks for your attention!

People who gave me money
• Foundational Questions Institute (FQXi) Grant
RFP1-06-006

People who gave me ofﬁce space when I didn’t have any
money
• Perimeter Institute
• University College London

�ݺ�ߣ

Imperial20101215

Recommended

More Related Content

Viewers also liked (7)

Similar to Imperial20101215 (8)

Imperial20101215