Index Numbers.ppt
- 2. INTRODUCTION ïĒ An index number measures the relative change in price, quantity, value, or some other item of interest from one time period to another. ïĒ A simple index number measures the relative change in one or more than one variable.
- 3. WHAT IS AN INDEX NUMBER . âĒ An index number measures how much a variable changes over time. âĒ We calculate the index number by finding the ratio of the current value to a base value.
- 4. DEFINITION ïĒ âIndex numbers are quantitative measures of growth of prices, production, inventory and other quantities of economic interest.â ï -Ronold
- 5. CHARACTERISTICS OF INDEX NUMBERS ïķ Index numbers are specialized averages. ïķ Index numbers are expressed in percentages ïķ Index numbers measure the change in the level of a phenomenon. ïķ Index numbers measure the effect of changes over a period of time.
- 6. USES OF INDEX NUMBERS o To framing suitable policies o They reveal trends and tendencies. o Index numbers help in measuring the purchasing power of money.
- 7. PROBLEMS RELATED TO INDEX NUMBERS ïĒ Choice of the base period. ïĒ Choice of an average. ïĒ Selection of formula ïĒ Selection of commodities. ïĒ Selection of data
- 8. CLASSIFICATION OF INDEX NUMBERS Price Index Quantity Index Value Index Composite Index
- 9. METHODS OF CONSTRUCTING INDEX NUMBERS Index Numbers Simple Aggregative Simple Average of Price Relative Unweighted Weighted Weighted Aggregated Weighted Average of Price Relatives
- 10. SIMPLE AGGREGATIVE METHOD It consists in expressing the aggregate price of all commodities in the current year as a percentage of the aggregate price in the base year. P01= Index number of the current year. = Total of the current yearâs price of all commodities. = Total of the base yearâs price of all commodities. 100 0 1 01 ïī ï― ïĨ ïĨ p p P 1 p 0 p
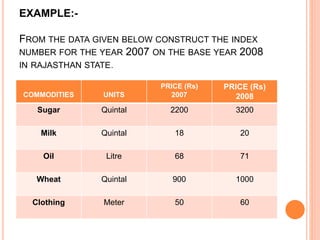
- 11. EXAMPLE:- FROM THE DATA GIVEN BELOW CONSTRUCT THE INDEX NUMBER FOR THE YEAR 2007 ON THE BASE YEAR 2008 IN RAJASTHAN STATE. COMMODITIES UNITS PRICE (Rs) 2007 PRICE (Rs) 2008 Sugar Quintal 2200 3200 Milk Quintal 18 20 Oil Litre 68 71 Wheat Quintal 900 1000 Clothing Meter 50 60
- 12. SOLUTION:- COMMODITIES UNITS PRICE (Rs) 2007 P0 PRICE (Rs) 2008 P1 Sugar Quintal 2200 3200 Milk Quintal 18 20 Oil Litre 68 71 Wheat Quintal 900 1000 Clothing Meter 50 60 3236 0 ï― ïĨp 4351 1 ï― ïĨp Index Number for 2008- 45 . 134 100 3236 4351 100 0 1 01 ï― ïī ï― ïī ï― ïĨ ïĨ p p P It means the prize in 2008 were 34.45% higher than the previous year.
- 14. SIMPLE AVERAGE OF RELATIVES METHOD. ïĒ The current year price is expressed as a price relative of the base year price. These price relatives are then averaged to get the index number. The average used could be arithmetic mean, geometric mean or even median. N p p P ïĨ ï· ï· ïļ ïķ ï§ ï§ ïĻ ïĶ ïī ï― 100 0 1 01 Where N is Numbers Of items. When geometric mean is used- N p p P ïĨ ï· ï· ïļ ïķ ï§ ï§ ïĻ ïĶ ïī ï― 100 log log 0 1 01
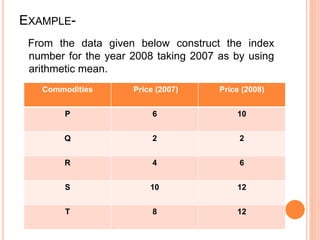
- 15. EXAMPLE- From the data given below construct the index number for the year 2008 taking 2007 as by using arithmetic mean. Commodities Price (2007) Price (2008) P 6 10 Q 2 2 R 4 6 S 10 12 T 8 12
- 16. SOLUTION- Index number using arithmetic mean- Commodities Price (2007) Price (2008) Price Relative P 6 10 166.7 Q 12 2 16.67 R 4 6 150.0 S 10 12 120.0 T 8 12 150.0 100 0 1 ïī p p ïĨ ï· ï· ïļ ïķ ï§ ï§ ïĻ ïĶ ïī100 0 1 p p =603.37 63 . 120 5 37 . 603 100 0 1 01 ï― ï― ï· ï· ïļ ïķ ï§ ï§ ïĻ ïĶ ïī ï― ïĨ N p p P 1 p 0 p
- 17. SIMPLE AVERAGE OF PRICE RELATIVES INDEX NUMBER USING GEOMETRIC MEAN Commoditi es Price (2007) Price (2008) Price Relative Log p P 6 10 166.7 2.2201 Q 12 2 16.7 1.2227 R 4 6 150.0 2.1761 S 10 12 120.0 2.0792 T 8 12 150.0 2.1761 p01 = antilog [ÎĢ log P / N] ÎĢ log P=9.8742 Po1= antilog(9.8742/5)= 1.9748 =antilog(1.9748) =9419+17 =94.36
- 18. ïĒ p01 = antilog [ÎĢ log P / N] ïĒ Po1= antilog(9.8742/5)= 1.9748 ïĒ =antilog(1.9748) ïĒ =9419+17 ïĒ =94.36
- 19. WEIGHTED INDEX NUMBERS ïĒ These are those index numbers in which rational weights are assigned to various chains in an explicit fashion. (A) Weighted aggregative index numbers- These index numbers are the simple aggregative type with the fundamental difference that weights are assigned to the various items included in the index. ï Dorbish and bowleyâs method. ï Fisherâs ideal method. ï Marshall-Edgeworth method. ï Laspeyres method. ï Paasche method. ï Kellyâs method.
- 20. LASPEYRES METHOD- This method was devised by Laspeyres in 1871. In this method the weights are determined by quantities in the base. 100 0 0 0 1 01 ïī ï― ïĨ ïĨ q p q p p Paascheâs Method. This method was devised by a German statistician Paasche in 1874. The weights of current year are used as base year in constructing the Paascheâs Index number. 100 1 0 1 1 01 ïī ï― ïĨ ïĨ q p q p p
- 21. DORBISH & BOWLEYS METHOD. This method is a combination of Laspeyreâs and Paascheâs methods. If we find out the arithmetic average of Laspeyreâs and Paascheâs index we get the index suggested by Dorbish & Bowley. Fisherâs Ideal Index. Fisherâs deal index number is the geometric mean of the Laspeyreâs and Paascheâs index numbers. 100 2 1 0 1 1 0 0 0 1 01 ïī ïŦ ï― ïĨ ïĨ ïĨ ïĨ q p q p q p q p p ïĨ ïĨ ïĨ ïĨ ïī ï― 1 0 1 1 0 0 0 1 01 q p q p q p q p P 100 ïī
- 22. MARSHALL-EDGEWORTH METHOD. In this index the numerator consists of an aggregate of the current years price multiplied by the weights of both the base year as well as the current year. Kellyâs Method. Kelly thinks that a ratio of aggregates with selected weights (not necessarily of base year or current year) gives the base index number. 100 1 0 0 0 1 1 0 1 01 ïī ïŦ ïŦ ï― ïĨ ïĨ ïĨ ïĨ q p q p q p q p p 100 0 1 01 ïī ï― ïĨ ïĨ q p q p p q refers to the quantities of the year which is selected as the base. It may be any year, either base year or current year.
- 23. EXAMPLE- Given below are the price quantity data,with price quoted in Rs. per kg and production in qtls. Find- (1) Laspeyers Index (2) Paascheâs Index (3)Fisher Ideal Index. ITEMS PRICE PRODUCTION PRICE PRODUCTION BEEF 15 500 20 600 MUTTON 18 590 23 640 CHICKEN 22 450 24 500 2002 2007
- 24. SOLUTION- ITEMS PRICE PRODUCT ION PRICE PRODU CTION BEEF 15 500 20 600 10000 7500 12000 9000 MUTTON 18 590 23 640 13570 10620 14720 11520 CHICKEN 22 450 24 500 10800 9900 12000 11000 TOTAL 34370 28020 38720 31520 ïĻ ïĐ 0 p ïĻ ïĐ 0 q ïĻ ïĐ 1 q ïĻ ïĐ 1 p ïĻ ïĐ 0 1q p ïĻ ïĐ 0 0q p ïĻ ïĐ 1 1q p ïĻ ïĐ 1 0q p
- 25. SOLUTION- 66 . 122 100 28020 34370 100 0 0 0 1 01 ï― ïī ï― ïī ï― ïĨ ïĨ q p q p p 2. Paascheâs Index : 84 . 122 100 31520 38720 100 1 0 1 1 01 ï― ïī ï― ïī ï― ïĨ ïĨ q p q p p 3. Fisher Ideal Index 100 ïī 69 . 122 100 31520 38720 28020 34370 ï― ïī ïī ï― ïĨ ïĨ ïĨ ïĨ ïī ï― 1 0 1 1 0 0 0 1 01 q p q p q p q p P 1.Laspeyres index:
- 26. WEIGHTED AVERAGE OF PRICE RELATIVE In weighted Average of relative, the price relatives for the current year are calculated on the basis of the base year price. These price relatives are multiplied by the respective weight of items. These products are added up and divided by the sum of weights. Weighted arithmetic mean of price relative- ïĨ ïĨ ï― V PV P01 100 0 1 ïī ï― P P P Where- P=Price relative V=Value weights= 0 0q p
- 27. VALUE INDEX NUMBERS Value is the product of price and quantity. A simple ratio is equal to the value of the current year divided by the value of base year. If the ratio is multiplied by 100 we get the value index number. 100 0 0 1 1 ïī ï― ïĨ ïĨ q p q p V
- 28. CHAIN INDEX NUMBERS When this method is used the comparisons are not made with a fixed base, rather the base changes from year to year. For example, for 2007,2006 will be the base; for 2006, 2005 will be the same and so on. Chain index for current year- 100 year previous of index Chain year current of relative link Average ïī ï―
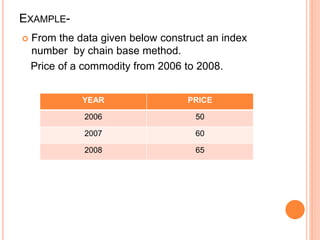
- 29. EXAMPLE- ïĒ From the data given below construct an index number by chain base method. Price of a commodity from 2006 to 2008. YEAR PRICE 2006 50 2007 60 2008 65
- 30. SOLUTION- YEAR PRICE LINK RELATIVE CHAIN INDEX (BASE 2006) 2006 50 100 100 2007 60 2008 65 120 100 50 60 ï― ïī 108 100 60 65 ï― ïī 120 100 100 120 ï― ïī 60 . 129 100 120 108 ï― ïī
- 31. REFERENCES 1. Statistics for management. Richard i. Levin & David S. Rubin. 2. Statistics for Business and economics. R.P.Hooda. 3. Business Statistics. B.M.Agarwal. 4. Business statistics. S.P.Gupta.














![SIMPLE AVERAGE OF PRICE RELATIVES INDEX
NUMBER USING GEOMETRIC MEAN
Commoditi
es
Price
(2007)
Price (2008) Price
Relative
Log p
P 6 10 166.7 2.2201
Q 12 2 16.7 1.2227
R 4 6 150.0 2.1761
S 10 12 120.0 2.0792
T 8 12 150.0 2.1761
p01 = antilog [ÎĢ log P / N]
ÎĢ log P=9.8742
Po1= antilog(9.8742/5)= 1.9748
=antilog(1.9748)
=9419+17
=94.36](https://image.slidesharecdn.com/indexnumbers-221115090604-cdabee5f/85/Index-Numbers-ppt-17-320.jpg)
![ïĒ p01 = antilog [ÎĢ log P / N]
ïĒ Po1= antilog(9.8742/5)= 1.9748
ïĒ =antilog(1.9748)
ïĒ =9419+17
ïĒ =94.36](https://image.slidesharecdn.com/indexnumbers-221115090604-cdabee5f/85/Index-Numbers-ppt-18-320.jpg)