Insertion & Selection Sort - using Priority Queues
- 1. Insertion & Selection Sort using priority queues By ŌĆō Priyanka Rana By PRIYANKA RANA Priyanka Rana ║▌║▌▀Żs
- 2. Implementing a Priority Queue ŌĆó With an unsorted list : ŌĆó insert() ŌĆō adds entry at last -> takes O(1) ŌĆó removeMin() ŌĆō requires complete scan -> takes O(n) ŌĆó ŌĆ£fast insertion and slow removalŌĆØ 4 5 2 3 1 Priyanka Rana ║▌║▌▀Żs
- 3. ’ü▒ With a Sorted List: ’ü▒ Insert() ŌĆō requires complete scan -> takes O(n) ’ü▒ removeMin() ŌĆō always access the first element -> takes O(1) ’ü▒ fast removal and slow insertions. 1 2 3 4 5 Priyanka Rana ║▌║▌▀Żs
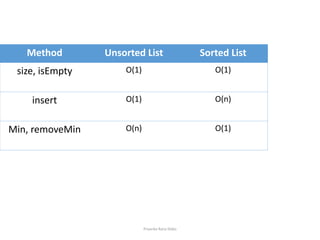
- 4. Method Unsorted List Sorted List size, isEmpty O(1) O(1) insert O(1) O(n) Min, removeMin O(n) O(1) Priyanka Rana ║▌║▌▀Żs
- 5. Sorting using priority Queues ŌĆó Selection ŌĆō Sort ŌĆó Insertion - Sort Priyanka Rana ║▌║▌▀Żs
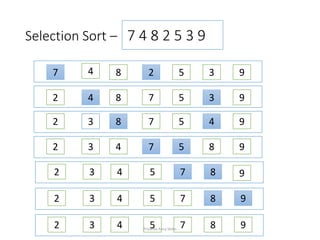
- 6. Selection Sort ŌĆō 7 4 8 2 5 3 9 7 4 8 2 5 3 9 2 4 8 7 5 3 9 2 3 8 7 5 4 9 2 3 4 7 5 8 9 2 3 4 5 7 8 9 2 3 4 5 7 8 9 2 3 4 5 7 8 9 Priyanka Rana ║▌║▌▀Żs
- 7. Selection- Sorting using priority Queues Sequence S Priority Queue P Input (7,4,8,2,5,3,9) () Phase 1 (a) (b) . . . (g) (4,8,2,5,3,9) (8,2,5,3,9) . . . () (7) (7,4) . . . (7,4,8,2,5,3,9) Phase 2 (a) (b) (c) (d) (e) (f) (g) (2) (2,3) (2,3,4) (2,3,4,5) (2,3,4,5,7) (2,3,4,5,7,8) (2,3,4,5,7,8,9) (7,4,8,2,5,3,9) (7,4,8,5,9) (7,8,5,9) (7,8,9) (8,9) (9) () Priyanka Rana ║▌║▌▀Żs
- 8. Running Time ŌĆó First removeMin takes O(n) time ŌĆó Second removeMin takes O(n-1) time) and so on ŌĆó Till last n operation takes O(1) time = O(n2)O(n Priyanka Rana ║▌║▌▀Żs
- 9. Insertion Sort ŌĆō 7 4 8 2 5 3 9 7 4 7 4 7 8 2 4 7 8 2 3 4 5 7 8 9 2 3 4 5 7 8 2 4 5 7 8 Priyanka Rana ║▌║▌▀Żs
- 10. Insertion -Sorting using priority Queues Sequence S Priority Queue P Input (7,4,8,2,5,3,9) () Phase 1 (a) (b) (c) (d) (e) (f) (g) (4,8,2,5,3,9) (8,2,5,3,9) (2,5,3,9) (5,3,9) (3,9) (9) () (7) (4,7) (4,7,8) (2,4,7,8) (2,4,5,7,8) (2,3,4,5,7,8) (2,3,4,5,7,8,9) Phase 2 (a) (b) . . . (g) (2) (2,3) . . . (2,3,4,5,7,8,9) (3,4,5,7,8,9) (4,5,7,8,9) . . . () Priyanka Rana ║▌║▌▀Żs
- 11. Running Time ŌĆó First element -no comparison ŌĆó Second element ŌĆō 1 comparison ŌĆó Third element ŌĆō 2 comparisons and so on. = O(n2)O(n Priyanka Rana ║▌║▌▀Żs
- 12. THANK YOU Priyanka Rana ║▌║▌▀Żs
Editor's Notes
- #3: In this session we'll learn how to implement a priority queue by storing its entries in a list S , where the list can be sorted or unsorted. for unsorted list, //simple way of performing insert operation is to add the element at the end of list , by executing method addLast().// This implementation of method insert takes O(1) time as inserting entries at the end of list does not take into account the ordering of the keys. To perform removeMin method , we have to inspect all the elements of list to find an entry with minimum k. So it taken O(n) time, where n is the number of entries, or data size.// So thats why implementation with an unsorted list is also called as "fast insertion and slow removal".
- #4: An alternative implementation of a priority queue is in a sorted list. ,// here insertion requires a complete scan of the list to find the appropriate position to insert the new entry so it takes O(n) time, while// removeMin method just needs to access the first element of the list as that will be the one which is least in the sorted list.and so it takes O(1) times.// it is also called as fast removal and slow insertions,
- #6: There are basically two most popular techniques for sorting, selection-sort and insertion-sort. Lets talk about each of this one by one.
- #7: In selection -sort ,// lets Consider we have to sort n numbers stored in array A by ’¼ürst ’¼ünding the smallest element of A and exchanging it with the element in A[0], the first element. Then ’¼ünding the second smallest element of A, and exchanging it with A[1], the second element. Continue in this manner for the ’¼ürst nŌłÆ1 elements of A. This method of sorting is known as selection sort.
- #8: In last session I mentioned about sorting using priority queus, through insert and removeMin() . Lets see how priority queues help in sorting, lets say we have some data in sequence S, and an empty priority queue, // Selection sort occurs in two phases, in first phase we insert all the elements in priority queue P using simple insert() method,// we ll pick first item// from the sequence insert into P,then second element// , third and so on, this way we have complete data in prority queue now, now in Phase 2 //we repeatedly remove the elements from P using the removeMin() method. we ll find the least element in the qyueue, and put it back in sequence S, // //, we ll do this till the last element in priority queue , when all the elements of queue are moved to sequence S in order. In this whole process bottleneck is in phase 2, where we repeatedly remove an entry with smallest key from Queue P. We start with priority queue size equals n and incrementally decreases with each removeMin until it becomes 0.
- #9: //Thus, the first removeMin operation takes time O(n) as there are n entries, then the second one// takes time O(n ŌłÆ 1) as one entry has already been moved to sequence S and so number of elements are (n-1) now and so on, //until the last (nth) operation takes time O(1). Therefore, //the total time needed for the second phase is //
- #10: Next is insertion sort: In insertion sort the ’¼ürst entry is always taken as sorted. // Insertion of the second entry requires one comparison with the first entry, in order to ’¼ünd its proper position. //Insertion of the third entry requires two comparisons, and // fourth entry requires three comparisons and so on. This method is known as insertion sort, where in each iteration, one entry is added to the sorted list. Inserting after comaprison
- #11: Insertion sort using priority queue is again a two phase process, : here we have a data set in sequence S, and // an empty priority queue P, In Phase 1, we remove the// first element of list and insert it into Priority queue P,, then second element// is removed from the sequence and we scan the data in priority queue , until we find the correct place for this element. , same step is repeated for //third element, it is compared with existing two elements in priority queue and placed at right position, and this is repeated for the whole data set.// // // In Phase 2, we call removeMin method on Priority queue repeatedly,// here because of phase 1 every time it returns the first element of the list and// // we add that element at the end of Sequence S, and this way we get sorted sequence S.
- #12: Analyzing the running time of this whole process, we see that phase 1 is the bottleneck of this sorting ,//as for placing first element , there is no comparison , //while for second element , there is 1 comparison and so on. and like selection sort, //insertion sort also runs in O(n2) time