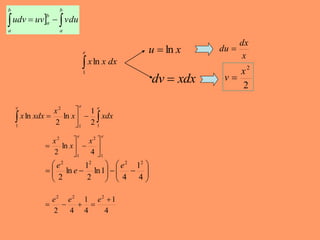More Related Content What's hot (20)
PDF
Resoluci├│n de sistema de ecuaciones cuadr├Īticas
Tamara Vargas ╠²
ODP
Ra├Łces racionales de polinomios - Teorema de Gauss
tboragini ╠²
PDF
CRITERIOS DE LA PRIMERA Y LA SEGUNDA DERIVADA
innovalabcun ╠²
Viewers also liked (10) PPT
Introduci├▓n a la integral definida
jucapama ╠²
PPT
III-3. Integral Definida - Área bajo la Curva
Ugma ╠²
PPTX
Shareslide presentation
ksross ╠²
More from Silver Mendoza A. (20)
PDF
Metodosymodelosdeinvestigaciondeoperaciones vol11-140228104929-phpapp02
Silver Mendoza A. ╠²
PDF
Ebert soria programa econ├│mico de latinoam├®rica 2c oportunidades y riesgos-...
Silver Mendoza A. ╠²
2. El teorema fundamental del c├Īlculo
ŌĆó Al momento de querer resolver una integral que tenga l├Łmites, integrales
definidas o de Riemann, por ser ├®ste matem├Ītico uno de los precursores de
este tipo de integrales.
ŌĆó El enunciado: Sea f una funci├│n continua en [a; b]. Entonces,
f (x)dx F(x)’üØ F(b) F(a) b
’ā▓ ’ĆĮ ’ĆĮ ’ĆŁ
a
b
a
donde: a = L├Łmite inferior y b = L├Łmite superior.
F├│rmula de Newton-Leibniz.
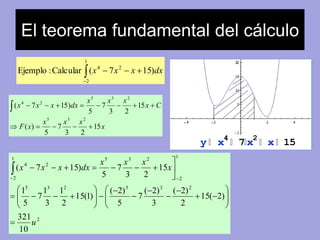
3. El teorema fundamental del c├Īlculo
4
y x
2
7 x
x 15
’ā╣
1
4 2 Ejemplo : Calcular (x 7x x 15)dx
’ā▓
’ĆŁ
’ĆŁ ’ĆŁ ’Ć½
2
5 3 2
x x x
’ā▓ ’ĆŁ ’ĆŁ ’Ć½ ’ĆĮ ’ĆŁ 7
’ĆŁ ’Ć½ ’Ć½
x
4 2
x x x dx
( 7 15)
5 3 2
x x x
F x
x C
15
’ā× ’ĆĮ ’ĆŁ ’ĆŁ ’Ć½
3 2
7
5
( )
15
3 2
5
5 3 2 5 3 2
’ā▓
’ā”
1
’ĆĮ ’ĆŁ 7
’ĆŁ ’Ć½
2
1
2
1 5 3 2
2
4 2
1
321
10
15( 2)
( 2)
2
( 2)
7
3
( 2)
5
15(1)
1
2
3
5
15
3 2
7
5
( 7 15)
u
x
x x x
x x x dx
’ĆĮ
’āČ
’āĘ ’āĘ
’āĖ
’ā”
’ā¦ ’ā¦
’ā©
’Ć½ ’ĆŁ
’ĆŁ
’ĆŁ
’ĆŁ
’ĆŁ
’ĆŁ
’āČ
’ĆŁ ’āĘ ’āĘ
’āĖ
’ā¦ ’ā¦
’ā©
’ā║’ā╗
’ĆŁ ’ĆŁ ’Ć½ ’ĆĮ ’ĆŁ ’ĆŁ ’Ć½
’ĆŁ ’ĆŁ
4. El teorema fundamental del c├Īlculo
1
4
’ā▓ ’Ć½
0
1
3
3
Ejemplo : Calcular (x 4x )dx
2
’āČ
’ā”
x x dx x x C
1
3
0
4
3
4
7
4
3
F x x x
’ā× ’ĆĮ ’Ć½
1 7
3
0
1
3
4
3
3
3
4
3
7
3
1
3
3
3
7
3
’ā╣
3 (1) ( 1)
3
7
( 4 )
3
7
( )
4
4
7
Se sabe que : ( 4 )
x x dx x x F F u
’ā║ ’ĆĮ ’ĆŁ ’ĆŁ ’ĆĮ
’ā╗
’Ć½ ’ĆĮ ’Ć½
’Ć½
’āĘ
’āĘ
’āĖ
’ā¦
’ā¦
’ā©
’Ć½ ’ĆĮ ’Ć½
’ā▓
’ā▓
5. ln 2
Ejemplo : Calcular e e dx x x
’ā▓ ’ĆŁ
1
2
ln
Log 2
Log
1
2
Exp x Exp x x
Soluci├│n
1. M├®todo a emplear: Integraci├│n Definida.
2. Regla de integraci├│n: Teorema fundamental del c├Īlculo(TFD)
3. Desarrollo:
’üØ
’ā▓ ’ĆĮ ’ā▓ ’ĆĮ ’ā▓ ’ĆĮ ’ĆŁ e e dx e dx dx x x x
1
’ĆĮ ’ĆŁ
2ln 2
1
2
ln 2 ln
ln 2
1
2
ln
ln 2
1
2
ln
ln 2
1
2
ln
0
ln 2
2
ln
’ĆĮ
0.5 1.0 1.5 2.0
1.0
0.8
0.6
0.4
0.2
In[38]:=
Log 2
Log
1
2
x
e
e
x
x
Out[38]= 2 Log 2
6. 3
’ā▓ ’Ć©’ĆŁ ’Ć½ ’ĆŁ ’Ć®
2 Ejemplo : Calcular x 4x 3 dx
1
Soluci├│n
1. M├®todo a emplear: Integraci├│n Definida.
2. Regla de integraci├│n: Teorema fundamental del c├Īlculo(TFD)
3. Desarrollo:
’Ć© ’Ć®
1
x x dx x x x
’ā”
’ĆĮ ’Ć½ ’ĆŁ
’Ć© ’Ć® ’Ć© ’Ć® ’Ć© ’Ć®
2
3 2
3
1
3 2
3
1
2
1
4
3
’ĆŁ ’Ć½ ’ĆŁ ’āĘ’āĖ
2 3
1
3
3 2 3 3 3
3
2 3
3
4 3
u
’ĆĮ
’ā╣
’āČ
’āĘ’āĖ
’ā”
’ā¦’ā©
’āČ
’ā¦’ā©
’ā║’ā╗
’ā▓ ’ĆŁ ’Ć½ ’ĆŁ ’ĆĮ ’Ć½ ’ĆŁ
2
In[2]:= ContourPlot y x
4 x 3, x 1, x 3 ,
x, 1, 4 , y, 1, 4 , Axes True, Frame False
Out[2]=
4
3
2
1
1 1 2 3 4
1
7. 2
Ejemplo: ’ā▓
dx
ln
e
e x x
dx e
’üØ
d ln
x
’ā▓ ’ĆĮ ’ā▓ ’ĆĮ
e e
’ĆĮ ’ĆŁ
ln(ln ) ln(ln )
ln 2 0.69
ln ln
ln
ln
2
2
2 2
’ĆĮ ’é╗
x
x
x x
e
e
e
e
e
Soluci├│n:
ContourPlot y
1
x Log x
2 4 6 8 10
2
1
1
2
3
4
5
In[68]:=
Exp 2 1
Exp 1
x Log x
x
Out[68]= Log 2
, x Exp 1 , x Exp 2 ,
x, 1, 10 , y, 5, 2 , Axes True,
Frame False
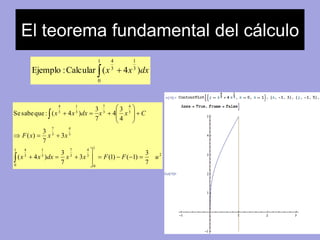
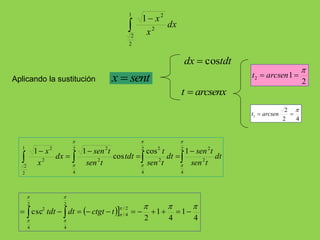
8. Cambio de variable en la integral definida
2
’ā▓ ’ĆĮ ’ā▓ ’éó
( ) ( ( )) ( )
1
t
t
b
a
f x dx f ՟ t ՟ t dt
Ejemplo:
’ĆŁ 1
’ā▓
2
2
2 1
2
dx
x
x
1 x2
x2
x, 2, 2 , y, 1, 10 , Axes True,
10
8
6
4
2
ContourPlot y
, x
2
2
, x 1 ,
Frame False
2 1 1 2
In[74]:=
1 1 x2
2
2
x2
x
Out[74]= 1
4
9. ’ā╣
’ā®
’āČ
’ā”
2 ’ü░
’ü░
I ’ā▓ sen x sen’ā®x ’ā╣ dx
’ā║
’ā╗
’ā¬
’ā½
’ā¬
’ĆŁ
’āĘ
’āĘ
’ĆŁ ’ā║
’āĖ
’ā¦
’ā¦
’ā©
’ĆĮ
2
1
2
2 2
’ā® ’ā╣
x x x
’ĆŁ ’éŻ ’éŻ ’ā× ’éŻ ’éŻ ’ā× ’ĆĮ
1 2 0 2 0
’ā╣
’ā®
’āČ
’ā”
2
2
I sen x sen dx
’ā▓
’ĆŁ
’āČ
’ā”
’ā¬
’ā½
1
2
I sen x dx
’ā▓
’ĆŁ
’āĘ ’āĘ
’āĖ
’ā¦ ’ā¦
’ā©
’ĆĮ
’ā║
’ā╗
’ā║
’ā¬
’ĆŁ
’āĘ ’āĘ
’āĖ
’ā¦ ’ā¦
’ā©
’ĆĮ
2
1
2 2
2
2
(0)
2
Soluci├│n
’ü░
’ü░
’ü░
2
u ’ĆĮ x ’ā× du ’ĆĮ dx ’ā× dx ’ĆĮ
du
’ü░
’ü░
2
’ü░
’ü░ ’ü░
2
2
2
x u
si 2
’ĆĮ ’ā× ’ĆĮ
x u
si 1
2
2
2
’ĆĮ ’ĆŁ ’ā× ’ĆĮ ’ĆŁ
2
2
2
’Ć© ’Ć® ’Ć© ’Ć® ’üØ
’ü░ ’ü░
2
I sen x dx sen u du sen u du u
’ā▓ ’ā▓ ’ā▓
’āČ
’āĘ
’āĘ
’āĖ
’ā”
’ā”
’ā¦
’ā¦
’āČ
2
’ĆĮ ’ĆŁ ’ĆŁ
’ā©
’ĆĮ ’ĆĮ ’ĆĮ
’āĘ
’āĘ
’āĖ
’ā¦
’ā¦
’ā©
’ĆĮ
’ĆŁ
2
’ĆŁ ’ĆŁ
’ĆŁ
2
’ü░ ’ü░
’ü░
’ü░ ’ü░ ’ü░
’ü░
’ü░
’ü░
’ü░
’ü░
2
cos cos
2
cos
2
2
2
2
2
2
2
2
2
2
1
I
10. ’ĆŁ 1
’ā▓
2
2
2 1
2
dx
x
x
Aplicando la sustituci├│n sent x ’ĆĮ
dx ’ĆĮ costdt
t ’ĆĮ arcsenx
2
2 4
1
’ü░
t ’ĆĮ arcsen ’ĆĮ
2
1 2
’ü░
t ’ĆĮ arcsen ’ĆĮ
1 2
2 2
2 2
’ĆŁ sen t
t
2
’ā▓ ’ā▓ ’ā▓ ’ā▓
’ĆŁ
’ĆĮ ’ĆĮ
’ĆŁ
’ĆĮ
4
sen t
2
4
2
4
2
2
2
2
2 cos 1
cos
1 1
’ü░
’ü░
’ü░
’ü░
’ü░
’ü░
dt
sen t
dt
sen t
tdt
sen t
dx
x
x
’Ć© ’Ć®’üØ
4
’ĆĮ ’ā▓ tdt ’ĆŁ ’ā▓ dt ’ĆĮ ’ĆŁ ctgt ’ĆŁ t ’ĆĮ ’ĆŁ ’Ć½ ’Ć½ ’ĆĮ 1
’ĆŁ
4
1
2
csc / 2
/ 4
2
4
2
4
2 ’ü░ ’ü░ ’ü░ ’ü░
’ü░
’ü░
’ü░
’ü░
’ü░
11. 3
’ā▓ ’Ć½
0
1dxx x
Aplicando la sustituci├│n z ’ĆĮ1’Ć½ x 2
dx ’ĆĮ 2zdz
z ’ĆĮ 1’Ć½ x
1 1 ’ĆĮ z
2 2 ’ĆĮ z
2
’ā▓ x ’Ć½ x dx ’ĆĮ ’ā▓ z ’ĆŁ z dz
1
4 2
3
0
1 2 ( )
In[13]:= ContourPlot y x 1 x , x 0, x 3 , x, 1, 5 , y, 1, 7 ,
Axes True, Frame False
Out[13]=
6
4
2
1 1 2 3 4 5
12. Integraci├│n por partes
b
’ā▓ ’ĆĮ ’üØ ’ĆŁ ’ā▓
a
b
b
a udv uv vdu
a
e
x xdx
1
Ejemplo : Calcular ln
’ā▓
In[78]:=
Exp 1
1
x Log x x
Out[78]=
1
4
1
2
In[23]:= ContourPlot y x Log x , x 1, x Exp 1 ,
x, 1, 4 , y, 1, 4 , Axes True, Frame False
x Log x x
Exp 1
1
x Log x x
Out[23]=
4
3
2
1
1 1 2 3 4
1
Out[24]=
x2
4
1
2
2
Log x
x
Out[25]=
1
4
1
2
13. 1
’ā▓
0
arctan xdx x
2
1
arctan
2
2
x
dv xdx v
dx
x
u x du
’ĆĮ ’ā× ’ĆĮ
’Ć½
’ĆĮ ’ā× ’ĆĮ
1
’ā▓ ’ā▓
’ā╣
’āČ
’ā”
’ā╣
’Ć© ’Ć®
1
2 4
arctan
1
1
2
arctan
2
1
1
1
2
arctan
2
2 1
arctan
2
arctan
1
0
1
0
2
1
0
2
1
0
2
1
0
2
2
1
0
1 2
0
’ü░
’ĆĮ ’ĆŁ ’Ć½
’ā║
’ā╗
’ā╣
’ā╣
’Ć½ ’ĆŁ ’ā║
’ā╗
’ĆĮ
’āĘ
’āĖ
’ā¦
’ā©
’Ć½
’ĆŁ ’ĆŁ ’ā║
’ā╗
’ĆĮ
dx
’Ć½
’ĆŁ ’ā║
’ā╗
’ĆĮ
’ā▓
x x x
x
dx
x
x
x
x
x x
x
x xdx
In[34]:= ContourPlot y x ArcTan x , x 2, x 2 3 ,
x, 4, 4 , y, 4, 4 , Axes True, Frame False
x ArcTan x x
1
x ArcTan x x
0
Out[34]=
4
2
4 2 2 4
2
4
Out[35]=
x
2
ArcTan x
2
1
2
2
ArcTan x
x
Out[36]=
1
4
2
14. b
’ā▓ ’ĆĮ ’üØ ’ĆŁ ’ā▓
a
b
b
a udv uv vdu
a
e
x x dx
1
’ā▓
ln
x u ln ’ĆĮ
dv ’ĆĮ xdx
dx
x
du ’ĆĮ
2 x
2
v ’ĆĮ
e e e
’ā╣
1
’ā▓ ’ā▓ ’ĆŁ ’ā║
’ā╗
’ĆĮ
x xdx
x
x xdx
1 1
2
ln
2
2
1 ln
e e
x
x
x
1
2
1
2
4
ln
2
’ā╣
’ā║
’ā╗
’ā╣
’ĆŁ ’ā║
’ā╗
’ĆĮ
’āČ
’āĘ ’āĘ
’āĖ
2 2 ’ā”
e
2 2 ’ĆŁ ’ĆŁ ’āĘ ’āĘ
’āĖ
’ā¦ ’ā¦
’ā©
’āČ
’ā”
’ĆĮ ’ĆŁ
’ā¦ ’ā¦
’ā©
1
4
4
1
ln1
2
ln
2
e
e
2 2 2 ’Ć½
4
1
e e 1
e
’ĆĮ ’ĆŁ ’Ć½ ’ĆĮ
4
2 4
15. b
’ā▓ ’ĆĮ ’üØ ’ĆŁ ’ā▓
a
b
b
a udv uv vdu
a
x u ’ĆĮ
dx du ’ĆĮ
x x dv e dx v e’ĆŁ ’ĆŁ ’ĆĮ ’ā× ’ĆĮ ’ĆŁ
1
xe dx x ’ā▓ ’ĆŁ
0
’Ć© ’Ć®’üØ ’Ć© ’Ć®
x x x
’ĆŁ ’ĆŁ ’ĆŁ ’ā▓ ’ā▓
xe dx x e e dx
’Ć© ’ĆŁ ’Ć®’üØ ’ĆŁ
’üØ
x e e
’ĆĮ ’ĆŁ ’ĆŁ
1 1
e e
’ĆĮ ’ĆŁ ’ĆŁ ’Ć½
’ĆĮ ’ĆŁ ’Ć½
’ĆĮ ’ĆŁ ’Ć½
0,74 1
2
1
0
1
0
1
0
1
0
1
0
0,26
1
2
1
u
e
x x
’ĆĮ
’ĆĮ ’ĆŁ ’ĆŁ ’ĆŁ
’ĆŁ ’ĆŁ

![El teorema fundamental del c├Īlculo
ŌĆó Al momento de querer resolver una integral que tenga l├Łmites, integrales
definidas o de Riemann, por ser ├®ste matem├Ītico uno de los precursores de
este tipo de integrales.
ŌĆó El enunciado: Sea f una funci├│n continua en [a; b]. Entonces,
f (x)dx F(x)’üØ F(b) F(a) b
’ā▓ ’ĆĮ ’ĆĮ ’ĆŁ
a
b
a
donde: a = L├Łmite inferior y b = L├Łmite superior.
F├│rmula de Newton-Leibniz.](https://image.slidesharecdn.com/integraldefinidaclase2-141026154127-conversion-gate02/85/Integral-definida-clase2-2-320.jpg)
![ln 2
Ejemplo : Calcular e e dx x x
’ā▓ ’ĆŁ
1
2
ln
Log 2
Log
1
2
Exp x Exp x x
Soluci├│n
1. M├®todo a emplear: Integraci├│n Definida.
2. Regla de integraci├│n: Teorema fundamental del c├Īlculo(TFD)
3. Desarrollo:
’üØ
’ā▓ ’ĆĮ ’ā▓ ’ĆĮ ’ā▓ ’ĆĮ ’ĆŁ e e dx e dx dx x x x
1
’ĆĮ ’ĆŁ
2ln 2
1
2
ln 2 ln
ln 2
1
2
ln
ln 2
1
2
ln
ln 2
1
2
ln
0
ln 2
2
ln
’ĆĮ
0.5 1.0 1.5 2.0
1.0
0.8
0.6
0.4
0.2
In[38]:=
Log 2
Log
1
2
x
e
e
x
x
Out[38]= 2 Log 2](https://image.slidesharecdn.com/integraldefinidaclase2-141026154127-conversion-gate02/85/Integral-definida-clase2-5-320.jpg)
![3
’ā▓ ’Ć©’ĆŁ ’Ć½ ’ĆŁ ’Ć®
2 Ejemplo : Calcular x 4x 3 dx
1
Soluci├│n
1. M├®todo a emplear: Integraci├│n Definida.
2. Regla de integraci├│n: Teorema fundamental del c├Īlculo(TFD)
3. Desarrollo:
’Ć© ’Ć®
1
x x dx x x x
’ā”
’ĆĮ ’Ć½ ’ĆŁ
’Ć© ’Ć® ’Ć© ’Ć® ’Ć© ’Ć®
2
3 2
3
1
3 2
3
1
2
1
4
3
’ĆŁ ’Ć½ ’ĆŁ ’āĘ’āĖ
2 3
1
3
3 2 3 3 3
3
2 3
3
4 3
u
’ĆĮ
’ā╣
’āČ
’āĘ’āĖ
’ā”
’ā¦’ā©
’āČ
’ā¦’ā©
’ā║’ā╗
’ā▓ ’ĆŁ ’Ć½ ’ĆŁ ’ĆĮ ’Ć½ ’ĆŁ
2
In[2]:= ContourPlot y x
4 x 3, x 1, x 3 ,
x, 1, 4 , y, 1, 4 , Axes True, Frame False
Out[2]=
4
3
2
1
1 1 2 3 4
1](https://image.slidesharecdn.com/integraldefinidaclase2-141026154127-conversion-gate02/85/Integral-definida-clase2-6-320.jpg)
![2
Ejemplo: ’ā▓
dx
ln
e
e x x
dx e
’üØ
d ln
x
’ā▓ ’ĆĮ ’ā▓ ’ĆĮ
e e
’ĆĮ ’ĆŁ
ln(ln ) ln(ln )
ln 2 0.69
ln ln
ln
ln
2
2
2 2
’ĆĮ ’é╗
x
x
x x
e
e
e
e
e
Soluci├│n:
ContourPlot y
1
x Log x
2 4 6 8 10
2
1
1
2
3
4
5
In[68]:=
Exp 2 1
Exp 1
x Log x
x
Out[68]= Log 2
, x Exp 1 , x Exp 2 ,
x, 1, 10 , y, 5, 2 , Axes True,
Frame False](https://image.slidesharecdn.com/integraldefinidaclase2-141026154127-conversion-gate02/85/Integral-definida-clase2-7-320.jpg)
![Cambio de variable en la integral definida
2
’ā▓ ’ĆĮ ’ā▓ ’éó
( ) ( ( )) ( )
1
t
t
b
a
f x dx f ՟ t ՟ t dt
Ejemplo:
’ĆŁ 1
’ā▓
2
2
2 1
2
dx
x
x
1 x2
x2
x, 2, 2 , y, 1, 10 , Axes True,
10
8
6
4
2
ContourPlot y
, x
2
2
, x 1 ,
Frame False
2 1 1 2
In[74]:=
1 1 x2
2
2
x2
x
Out[74]= 1
4](https://image.slidesharecdn.com/integraldefinidaclase2-141026154127-conversion-gate02/85/Integral-definida-clase2-8-320.jpg)

![3
’ā▓ ’Ć½
0
1dxx x
Aplicando la sustituci├│n z ’ĆĮ1’Ć½ x 2
dx ’ĆĮ 2zdz
z ’ĆĮ 1’Ć½ x
1 1 ’ĆĮ z
2 2 ’ĆĮ z
2
’ā▓ x ’Ć½ x dx ’ĆĮ ’ā▓ z ’ĆŁ z dz
1
4 2
3
0
1 2 ( )
In[13]:= ContourPlot y x 1 x , x 0, x 3 , x, 1, 5 , y, 1, 7 ,
Axes True, Frame False
Out[13]=
6
4
2
1 1 2 3 4 5](https://image.slidesharecdn.com/integraldefinidaclase2-141026154127-conversion-gate02/85/Integral-definida-clase2-11-320.jpg)
![Integraci├│n por partes
b
’ā▓ ’ĆĮ ’üØ ’ĆŁ ’ā▓
a
b
b
a udv uv vdu
a
e
x xdx
1
Ejemplo : Calcular ln
’ā▓
In[78]:=
Exp 1
1
x Log x x
Out[78]=
1
4
1
2
In[23]:= ContourPlot y x Log x , x 1, x Exp 1 ,
x, 1, 4 , y, 1, 4 , Axes True, Frame False
x Log x x
Exp 1
1
x Log x x
Out[23]=
4
3
2
1
1 1 2 3 4
1
Out[24]=
x2
4
1
2
2
Log x
x
Out[25]=
1
4
1
2](https://image.slidesharecdn.com/integraldefinidaclase2-141026154127-conversion-gate02/85/Integral-definida-clase2-12-320.jpg)
![1
’ā▓
0
arctan xdx x
2
1
arctan
2
2
x
dv xdx v
dx
x
u x du
’ĆĮ ’ā× ’ĆĮ
’Ć½
’ĆĮ ’ā× ’ĆĮ
1
’ā▓ ’ā▓
’ā╣
’āČ
’ā”
’ā╣
’Ć© ’Ć®
1
2 4
arctan
1
1
2
arctan
2
1
1
1
2
arctan
2
2 1
arctan
2
arctan
1
0
1
0
2
1
0
2
1
0
2
1
0
2
2
1
0
1 2
0
’ü░
’ĆĮ ’ĆŁ ’Ć½
’ā║
’ā╗
’ā╣
’ā╣
’Ć½ ’ĆŁ ’ā║
’ā╗
’ĆĮ
’āĘ
’āĖ
’ā¦
’ā©
’Ć½
’ĆŁ ’ĆŁ ’ā║
’ā╗
’ĆĮ
dx
’Ć½
’ĆŁ ’ā║
’ā╗
’ĆĮ
’ā▓
x x x
x
dx
x
x
x
x
x x
x
x xdx
In[34]:= ContourPlot y x ArcTan x , x 2, x 2 3 ,
x, 4, 4 , y, 4, 4 , Axes True, Frame False
x ArcTan x x
1
x ArcTan x x
0
Out[34]=
4
2
4 2 2 4
2
4
Out[35]=
x
2
ArcTan x
2
1
2
2
ArcTan x
x
Out[36]=
1
4
2](https://image.slidesharecdn.com/integraldefinidaclase2-141026154127-conversion-gate02/85/Integral-definida-clase2-13-320.jpg)