�ݺ�ߣ

UD2: ANALISI MATEMATIKOA
INTEGRAZIOA

1. INTEGRAL MUGAGABEA.
2

1.1. Funtzio baten jatorrizkoa.
[a, b] tartean definituta dauden f(x) eta F(x) bi funtzio izanik, esango
dugu F(x) funtzioa f(x)-ren jatorrizko funtzioa dela, baldin eta F(x)-ren
deribatua f(x) bada tartean.

Demagun F(x) funtzioa f(x)-ren jatorrizkoa dela [a,b] tartean; f(x)-ren
integral mugagabea deritzogu haren jatorrizko guztien multzoari, F(x)
+ K eta honela adierazten dugu:

1.3. Integral mugagabeen propietateak.

2

1.4. Integral motak.

2

1.4.1. Deskonposizio bidezko integralak.

af ( x )

bg ( x ) dx

a

f ( x ) dx

b

g ( x ) dx


2

1.4.2. Ordezkapen metodoa.


2

1.4.3. Zatikako integrazio metodoa.


2

1.4.4. Funtzio razionalen integrazioa.


2

1.4.5. Funtzio Trigonometrikoen integrazioa.

1
2

2. INTEGRAL MUGATUA.
2.1. Kurba baten azpiko azalera.

3
4

Weierstrass- en teorema:
F(x) funtzioa jarraitua bada [a,b] tartean, tarte horretako bi puntutan
f(x) funtzioak maximoa eta minimoa ditu.
Tarte horretan funtzioak duen maximoari M deituko diogu eta
minimoari, m

1
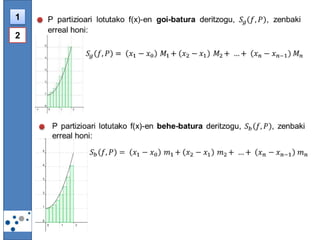
2

[a,b] tartean jarraitua den f funtzio bat izanik, f-ren integral mugatua
[a,b]-n deritzogu goi eta behe baturek biek duten limiteari, eta honela
adierazten dugu:

1

2.2. Funtzio integrala.

2

Barrow-ren erregela:
Izan bedi f(x) funtzioa jarraitua [a,b]-n, eta F(x), f(x)-en jatorrizkoa
[a,b]-n. Orduan;

Integral mugatuen propietateak:

1
2

2.3. Eskualde lau baten azalera.
F(x) funtzioa jarraitua eta positiboa bada [a,b]-n;
F(x)-en grafikoak, x=a eta x=b zuzenen eta abzisa ardatzak
mugatzen duten eskualdearen azalera adierazpen hinek
emandakoa da:

1
2


F(x) funtzioa jarraitua, postiboa eta negatiboa bada [a,b]-n;

1
2


f(x) eta g(x) funtzioa jarraituak, [a,b]-n;

�ݺ�ߣ

MATEMATIKA BATXI 2 UD2 Integralak

More Related Content

MATEMATIKA BATXI 2 UD2 Integralak