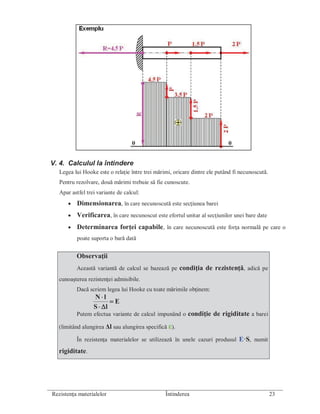
Intindere
- 1. ________________________________________________________________________________ Rezisten釘a materialelor ntinderea 21 V. NTINDEREA V. 1. Mrimi utilizate Simbolul Denumirea Unitatea de msur l lungimea ini釘ial mm l alungirea mm la alungirea admisibil mm lef alungirea efectiv mm S sec釘iunea mm2 Sef sec釘iunea efectiv mm2 Snec sec釘iunea necesar mm2 N for釘a normal N Ncap for釘a normal capabil N 竜 alungirea specific efortul unitar at efortul unitar admisibil la trac釘iune (rezisten釘a admisibil) ef efortul unitar efectiv E modulul de elasticitate longitudinal ES rigiditatea N V. 2. Generalit釘i O bar dreapt este solicitat la 樽ntindere c但nd la capetele ei sunt aplicate, 樽n lungul axei, dou for釘e egale de sens contrar 樽ndreptate spre exterior. OBSERVA鄭IE Pentru simplificare am reprezentat alungirea numai la un capt al barei.
- 2. ________________________________________________________________________________ Rezisten釘a materialelor ntinderea 22 Exist o asemnare a solicitrii la 樽ntindere cu experimentul de la capitolul Legea lui Hooke? Observa釘ie Este acelai experiment: 樽n locul captului fix am reprezentat o reac釘iune, egal i de sens contrar cu ac釘iunea. Prin urmare sunt valabile mrimile prin care am exprimat legea lui Hooke (domeniul elastic). Conform ipotezei lui Bernoulli, dac sec釘iunile rm但n plane, alungirile l sunt constante pe suprafa釘a sec釘iunii; 樽n consecin釘 i alungirile specifice 竜 sunt constante pe toat sec釘iunea. Aplic但nd legea lui Hooke, , rezult c i efortul unitar este constant pe sec釘iune. n concluzie: efortul unitar este constant pe sec釘iunea unei bare omogene. V. 3. Diagrama for釘elor normale Dac asupra unei bare drepte ac釘ioneaz mai multe for釘e de 樽ntindere, este necesar construc釘ia unei diagrame a for釘elor normale, care s arate 樽n ce sec釘iuni aceste for釘e sunt mai periculoase. Reguli de trasare 1. Diagrama se traseaz la o scar a for釘elor, reprezentate perpendicular pe axa barei. 2. Construc釘ia 樽ncepe de la un capt al liniei de referin釘, consider但nd pozitive for釘ele 樽nt但lnite, dac tind s lungeasc bara. 3. ntro sec釘iune oarecare, for釘a axial este dat de suma for釘elor situate de o parte a sec釘iunii (sau suma for釘elor de cealalt parte a sec釘iunii, cu semn schimbat). l S l N S N l l = =竜 E= 竜 E竜=
- 3. ________________________________________________________________________________ Rezisten釘a materialelor ntinderea 23 V. 4. Calculul la 樽ntindere Legea lui Hooke este o rela釘ie 樽ntre trei mrimi, oricare dintre ele put但nd fi necunoscut. Pentru rezolvare, dou mrimi trebuie s fie cunoscute. Apar astfel trei variante de calcul: Dimensionarea, 樽n care necunoscut este sec釘iunea barei Verificarea, 樽n care necunoscut este efortul unitar al sec釘iunilor unei bare date Determinarea for釘ei capabile, 樽n care necunoscut este for釘a normal pe care o poate suporta o bar dat Observa釘ii Aceast variant de calcul se bazeaz pe condi釘ia de rezisten釘, adic pe cunoaterea rezisten釘ei admisibile. Dac scriem legea lui Hooke cu toate mrimile ob釘inem: Putem efectua variante de calcul impun但nd o condi釘ie de rigiditate a barei (limit但nd alungirea l sau alungirea specific 竜). n rezisten釘a materialelor se utilizeaz 樽n unele cazuri produsul E揃S, numit rigiditate. E lS lN =
- 4. ________________________________________________________________________________ Rezisten釘a materialelor ntinderea 24 V. 5. Mersul calculelor V. 5. 1. Condi釘ia de rezisten釘 Dimensionarea 1. Se d for釘a N 2. Se alege un material pentru care se determin, din tabelul de materiale sau pe baza coeficientului de siguran釘, rezisten釘a admisibil at 3. Se calculeaz sec釘iunea necesar, care reprezint valoarea minim posibil pentru bar: 4. Valoarea ob釘inut se convertete la sec釘iunea unui profil standardizat, rotunjit prin mrire. Verificarea 1. Se dau: for釘a N sec釘iunea efectiv a barei Sef materialul barei 2. Se determin, din tabelul de materiale, rezisten釘a admisibil at 3. Se calculeaz efortul unitar efectiv din bar: 4. Se compar cele dou eforturi unitare Dac: ef at bara verific ef > at bara nu verific Determinarea for釘ei capabile 1. Se dau: sec釘iunea efectiv a barei Sef materialul barei 2. Se determin, din tabelul de materiale sau pe baza coeficientului de siguran釘, rezisten釘a admisibil at 3. Se calculeaz for釘a capabil a barei, care reprezint valoarea maxim posibil pentru bar: V. 5. 2. Condi釘ia de rigiditate Considerm c se impune o valoare admisibil pentru alungire la, care apare 樽n toate cazurile. Dimensionarea 1. Se dau: for釘a N lungimea barei l 2. Se alege un material pentru care se determin, din tabelul de materiale, modulul de elasticitate longitudinal E at nec N S ef ef S N = atefcap SN
- 5. ________________________________________________________________________________ Rezisten釘a materialelor ntinderea 25 at nec N S ef ef S N = atefcap SN a nec lE lN S ES lN l ef ef = l lES N aef cap E lS lN = E= 竜 3. Se calculeaz sec釘iunea necesar, care reprezint valoarea minim posibil pentru bar: 4. Valoarea ob釘inut se convertete la sec釘iunea unui profil standardizat, rotunjit prin mrire. Verificarea 1. Se dau: for釘a N lungimea barei l sec釘iunea efectiv a barei Sef materialul barei 2. Se determin, din tabelul de materiale, modulul de elasticitate longitudinal E 3. Se calculeaz alungirea efectiv a barei: 4. Dac: lef la bara verific lef > la bara nu verific Determinarea for釘ei capabile 1. Se dau: lungimea barei l sec釘iunea efectiv a barei Sef materialul barei 2. Se determin, din tabelul de materiale, modulul de elasticitate longitudinal E 3. Se calculeaz for釘a capabil a barei, care reprezint valoarea maxim posibil pentru bar: V. 6. Sinteza solicitrii Legea lui Hooke (domeniul elastic) Felul calculului Condi釘ia de rezisten釘 Condi釘ia de rigiditate Dimensionarea Verificarea Determinarea for釘ei capabile a nec lE lN S ES lN l ef ef = l lES N aef cap
- 6. ________________________________________________________________________________ Rezisten釘a materialelor ntinderea 26 nec nec nec l S l 12mm V. 7. Aplica釘ii I. S se dimensioneze la 樽ntindere o bar solicitat de for釘a normal N = 20.000 N Rezolvare: Problema se bazeaz pe condi釘ia de rezisten釘. 1. Se d for釘a N = 20.000 N 2. Din Tabelul nr.1 alegem un o釘el carbon OL 37, pentru care apreciem at = 120 3. Se calculeaz sec釘iunea necesar, care reprezint valoarea minim posibil pentru bar: Snec > 166,67 mm2 4. Stabilim ca sec釘iunea barei s fie rotund i calculm diametrul necesar: Semifabricatul din o釘el standardizat cel mai apropiat de valoarea calculat (din tabelele de standarde) este o釘elul rotund 15. II. S se dimensioneze la 樽ntindere o bar din o釘el OL 50, de sec釘iune ptrat, solicitat de for釘a normal N = 12.000 N, cunosc但nduse coeficientul de siguran釘 C = 6 Rezolvare: Problema se bazeaz pe condi釘ia de rezisten釘. 1. Se d for釘a N = 12.000 N 2. Pentru OL 50, valoarea minim a rezisten釘ei la rupere este r = 500 (Tabelul nr.1), de unde rezult rezisten釘a admisibil: 3. Se calculeaz sec釘iunea necesar, care reprezint valoarea minim posibil pentru bar: Snec > 144 mm2 4. Calculm latura ptratului necesar: 120 000.20 Snec nec nec nec 4 S d d 14,56mm nec 12.000 S 83,3 r at at 2 C 500 N 83,3 6 mm = = =
- 7. ________________________________________________________________________________ Rezisten釘a materialelor ntinderea 27 III. S se verifice o bar din o釘el lat laminat la cald 80x16 STAS 39577/OL 37 STAS 500 68 solicitat de for釘a normal de 樽ntindere N = 120.000 N Rezolvare: Problema se bazeaz pe condi釘ia de rezisten釘. 1. Cunoatem for釘a normal i materialul barei dar trebuie s calculm sec釘iunea efectiv: Sef = 80揃16 = 1.280 mm2 2. Din Tabelul nr.1 apreciem, pentru OL 37 at = 120 3. Calculm efortul unitar efectiv 樽n bar: 4. Comparm cele dou eforturi unitare: 93,7 < 120 Bara verific. IV. S se determine for釘a normal capabil a unei 釘evi din OL 50, av但nd diametrul exterior D = 40 mm i grosimea peretelui g = 3 mm. Rezolvare: Problema se bazeaz pe condi釘ia de rezisten釘. 1. Cunoatem materialul barei dar trebuie s calculm sec釘iunea efectiv: 2. Din Tabelul nr.1 apreciem, pentru OL 50 at = 150 3. Calculm for釘a normal capabil: V. S se dimensioneze la 樽ntindere o bar din aluminiu turnat cu lungimea l = 0,8 m, astfel 樽nc但t la solicitarea cu o for釘 normal N = 60.000 N s nu depeasc alungirea la = 1,5 mm. Rezolvare: Problema se bazeaz pe condi釘ia de rigiditate. 1. Se dau: for釘a N = 60.000 N lungimea barei l = 800 mm 2. Materialul fiind dat, extragem din tabelul de materiale valoarea modulului de elasticitate longitudinal E = 68.000 2ef ef mm N 7,93 280.1 000.120 = = ( )2 2 2 ef 40 32 S 452,39 mm 4 = = cap cap N 452,39 150 N 87.890N
- 8. ________________________________________________________________________________ Rezisten釘a materialelor ntinderea 28 3. Calculm sec釘iunea necesar: 4. Stabilim ca sec釘iunea barei s fie rotund i calculm diametrul necesar: Semifabricatul din o釘el standardizat cel mai apropiat de valoarea calculat (din tabelele de standarde) este aluminiul rotund 25. VI. O bar 40 din OL 70 cu lungimea l = 300 mm este solicitat la 樽ntindere de for釘a normal N = 50.000 N. S se verifice dac nu depete alungirea admisibil la = 0,2 mm. Rezolvare: Problema se bazeaz pe condi釘ia de rigiditate. 1. Cunoatem for釘a normal, lungimea i materialul dar trebuie s calculm sec釘iunea efectiv: Sef = 402 = 1.600 mm2 2. Din Tabelul nr.1 scoatem, pentru OL 70, valoarea modulului de elasticitate longitudinal E = 205.000 3. Calculm alungirea efectiv a barei: 4. Comparm cele dou alungiri: 0,04 < 0,2 Bara verific. VII. S se determine for釘a normal la 樽ntindere de care este capabil o bar 80 din bronz Bz12T lung de 1,3 m, astfel ca s nu depeasc alungirea de 0,4 mm. Rezolvare: Problema se bazeaz pe condi釘ia de rigiditate. 1. Cunoatem lungimea i materialul barei dar trebuie s calculm sec釘iunea efectiv: 2. Din Tabelul nr.1 scoatem, pentru Bz12T, valoarea modulului de elasticitate longitudinal E = 115.000 2 nec nec mm58,470S 5,1000.68 800000.60 S nec nec nec 4 S d d 14,56 mm mm04,0l 000.205600.1 300000.50 l ef ef = = 2 ef 80S 4 = 2 efS 5.026,55 mm=
- 9. ________________________________________________________________________________ Rezisten釘a materialelor ntinderea 29 3. Calculm for釘a normal capabil: cap cap 5.026,55 115.000 0,4 N 1.200 N 192.680 N