Introduction to crystallography and x ray diffraction theory
Download as PPTX, PDF
0 likes93 views
The crystal structure of a material determines its X-ray diffraction pattern. Quartz and cristobalite, two forms of SiO2, have different crystal structures and thus produce different diffraction patterns, even though they are chemically identical. Amorphous glass does not have long-range atomic order and so produces a broad diffraction peak rather than distinct peaks. The positions and intensities of peaks in a diffraction pattern provide information about a material's crystal structure, including the arrangement of atoms in the unit cell and the distances between planes of atoms.
![Parallel planes of atoms intersecting the unit cell define
directions and distances in the crystal.
The Miller indices (hkl) define the reciprocal of the axial intercepts
The crystallographic direction, [hkl], is the vector normal to (hkl)
dhkl is the vector extending from the origin to the plane (hkl) and is normal to (hkl)
The vector dhkl is used in Braggs law to determine where diffraction peaks will be
The (200) planes
of atoms in NaCl
The (220) planes
of atoms in NaCl](https://image.slidesharecdn.com/introductiontocrystallographyandx-raydiffractiontheory1-200219093112/85/Introduction-to-crystallography-and-x-ray-diffraction-theory-23-320.jpg)
![A Brief Introduction to Miller Indices
The Miller indices (hkl) define the reciprocal axial
intercepts of a plane of atoms with the unit cell
The (hkl) plane of atoms intercepts the unit cell at a/,
/, and /
The (220) plane drawn to the right intercepts the unit
cell at 遜a, 遜b, and does not intercept the c-axis. When a plane is parallel to
an axis assumed to intercept at ; therefore its
reciprocal is 0
The vector dhkl is drawn from the origin of the unit cell
to intersect the crystallographic plane (hkl) at a 90属.
The direction of dhkl is the crystallographic direction.
The crystallographic direction is expressed using [] brackets, such as [220]](https://image.slidesharecdn.com/introductiontocrystallographyandx-raydiffractiontheory1-200219093112/85/Introduction-to-crystallography-and-x-ray-diffraction-theory-26-320.jpg)
![Braggs law provides a simplistic model to understand
what conditions are required for diffraction.
For parallel planes of atoms, with a space dhkl between the planes, constructive
interference only occurs when Braggs law is satisfied.
In our diffractometers, the X-ray wavelength l is fixed.
Consequently, a family of planes produces a diffraction peak only at a specific angle 2q.
Additionally, the plane normal [hkl] must be parallel to the diffraction vector s
Plane normal [hkl]: the direction perpendicular to a plane of atoms
Diffraction vector s: the vector that bisects the angle between the incident and diffracted beam
Braggs Law
了= 2dhkl](https://image.slidesharecdn.com/introductiontocrystallographyandx-raydiffractiontheory1-200219093112/85/Introduction-to-crystallography-and-x-ray-diffraction-theory-27-320.jpg)
Introduction to crystallography and x ray diffraction theory
- 1. Effect of Mineral's Crystal Structure on X-Ray Diffraction Test Senior Chemical Engineer Raghd Muhi Al-Deen Jassim
- 3. Diffraction occurs when light is scattered by a periodic array with long-range order, producing constructive interference at specific angles. The electrons in an atom coherently scatter light. We can regard each atom as a coherent point scatterer The strength with which an atom scatters light is proportional to the number of electrons around the atom. The atoms in a crystal are arranged in a periodic array and thus can diffract light. The wavelength of X rays are similar to the distance between atoms. The scattering of X-rays from atoms produces a diffraction pattern, which contains information about the atomic arrangement within the crystal
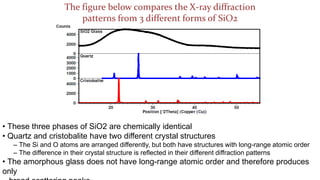
- 4. The figure below compares the X-ray diffraction patterns from 3 different forms of SiO2 These three phases of SiO2 are chemically identical Quartz and cristobalite have two different crystal structures The Si and O atoms are arranged differently, but both have structures with long-range atomic order The difference in their crystal structure is reflected in their different diffraction patterns The amorphous glass does not have long-range atomic order and therefore produces only
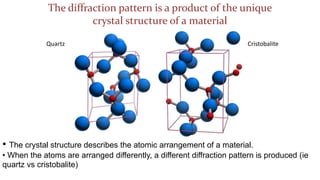
- 5. The diffraction pattern is a product of the unique crystal structure of a material Quartz Cristobalite The crystal structure describes the atomic arrangement of a material. When the atoms are arranged differently, a different diffraction pattern is produced (ie quartz vs cristobalite)
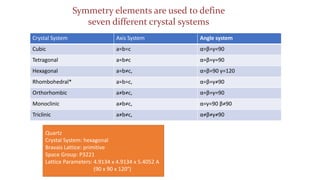
- 6. Crystalline materials are characterized by the long range orderly periodic arrangements of atoms. The unit cell is the basic repeating unit that defines the crystal structure. The unit cell contains the maximum symmetry that uniquely defines the crystal structure. The unit cell might contain more than one molecule: for example, the quartz unit cell contains 3 complete molecules of SiO2. The crystal system describes the shape of the unit cell The lattice parameters describe the size of the unit cell The unit cell repeats in all dimensions to fill space and produce the macroscopic grains or crystals of the material Crystal System: hexagonal Lattice Parameters: 4.9134 x 4.9134 x 5.4052 A (90 x 90 x 120属)
- 7. Crystal System Axis System Angle system Cubic a=b=c 留=硫=粒=90 Tetragonal a=bc 留=硫=粒=90 Hexagonal a=bc, 留=硫=90 粒=120 Rhombohedral* a=b=c, 留=硫=粒90 Orthorhombic abc, 留=硫=粒=90 Monoclinic abc, 留=粒=90 硫90 Triclinic abc, 留硫粒90 Quartz Crystal System: hexagonal Bravais Lattice: primitive Space Group: P3221 Lattice Parameters: 4.9134 x 4.9134 x 5.4052 A (90 x 90 x 120属) Symmetry elements are used to define seven different crystal systems
- 8. How are Crystal Systems Defined? There are six crystal systems. All minerals form crystals in one of these six systems. Although you may have seen more than six shapes of crystals, theyre all variations of one of these six habits. Each system is defined by a combination of three factors: How many axes it has. The lengths of the axes. The angles at which the axes meet. An axis is a direction between the sides. The shortest one is A. The longest is C. There is a B axis as well and sometimes a D axis.
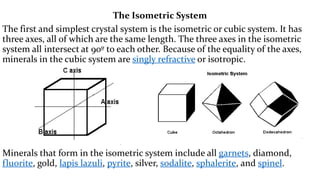
- 9. The Isometric System The first and simplest crystal system is the isometric or cubic system. It has three axes, all of which are the same length. The three axes in the isometric system all intersect at 90尊 to each other. Because of the equality of the axes, minerals in the cubic system are singly refractive or isotropic. Minerals that form in the isometric system include all garnets, diamond, fluorite, gold, lapis lazuli, pyrite, silver, sodalite, sphalerite, and spinel.
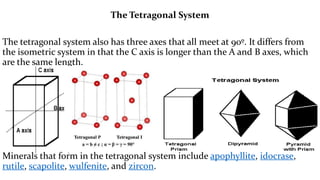
- 11. The Tetragonal System The tetragonal system also has three axes that all meet at 90尊. It differs from the isometric system in that the C axis is longer than the A and B axes, which are the same length. Minerals that form in the tetragonal system include apophyllite, idocrase, rutile, scapolite, wulfenite, and zircon.
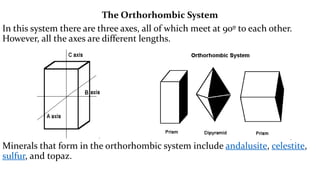
- 12. The Orthorhombic System In this system there are three axes, all of which meet at 90尊 to each other. However, all the axes are different lengths. Minerals that form in the orthorhombic system include andalusite, celestite, sulfur, and topaz.
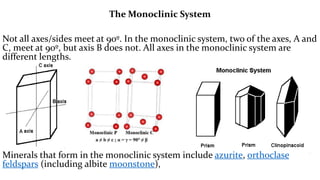
- 14. The Monoclinic System Not all axes/sides meet at 90尊. In the monoclinic system, two of the axes, A and C, meet at 90尊, but axis B does not. All axes in the monoclinic system are different lengths. Minerals that form in the monoclinic system include azurite, orthoclase feldspars (including albite moonstone),
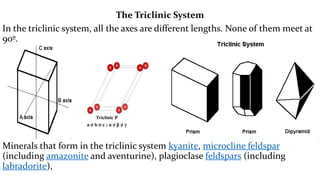
- 15. The Triclinic System In the triclinic system, all the axes are different lengths. None of them meet at 90尊. Minerals that form in the triclinic system kyanite, microcline feldspar (including amazonite and aventurine), plagioclase feldspars (including labradorite),
- 16. The Hexagonal System The crystal systems previously discussed represent every variation of four- sided figures with three axes. In the hexagonal system, we have an additional axis, which gives the crystals six sides. Three of these are equal in length and meet at 60尊 to each other. The C or vertical axis is at 90尊 to the shorter axes. Minerals that form in the hexagonal system include apatite, beryl (including aquamarine, emerald, heliodor, and morganite), taaffeite, and zincite.
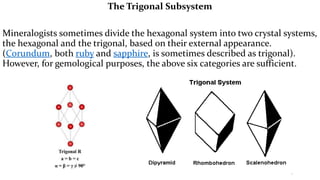
- 17. The Trigonal Subsystem Mineralogists sometimes divide the hexagonal system into two crystal systems, the hexagonal and the trigonal, based on their external appearance. (Corundum, both ruby and sapphire, is sometimes described as trigonal). However, for gemological purposes, the above six categories are sufficient.
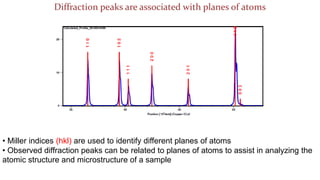
- 18. Diffraction peaks are associated with planes of atoms Miller indices (hkl) are used to identify different planes of atoms Observed diffraction peaks can be related to planes of atoms to assist in analyzing the atomic structure and microstructure of a sample
- 19. Miller Indices A workable symbolism results for the orientation of a plane in a lattice, the Miller indices, which are defined as the reciprocals of the fractional intercepts which the plane makes with the crystallographic axes. For example, if the Miller indices of a plane are (hkl), written in parentheses, then the plane makes fractional intercepts of l/h, l/k, l/l with the axes, and, if the axial lengths are a, b, c, the plane makes actual intercepts of a/h, b/k, c/l. Parallel to any plane in any lattice, there is a whole set of parallel equidistant planes, one of which passes through the origin; the Miller indices (hkl) usually refer to that plane in the set which is nearest the origin, although they may be taken as referring to any other plane in the set or to the whole set taken together.
- 20. Miller Indices
- 22. The result is that every set of planes will be able to diffract. The relation between the peaks positions, intensity, and shape of the diffraction pattern is a mixing of the position of every single atom, as well as the length of lattice parameters. It means that any calculation of the intensity gets started with structure factor because it contains information about the atomic base of the crystal and the electronic density.
- 23. Parallel planes of atoms intersecting the unit cell define directions and distances in the crystal. The Miller indices (hkl) define the reciprocal of the axial intercepts The crystallographic direction, [hkl], is the vector normal to (hkl) dhkl is the vector extending from the origin to the plane (hkl) and is normal to (hkl) The vector dhkl is used in Braggs law to determine where diffraction peaks will be The (200) planes of atoms in NaCl The (220) planes of atoms in NaCl
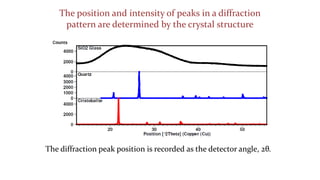
- 24. The position and intensity of peaks in a diffraction pattern are determined by the crystal structure The diffraction peak position is recorded as the detector angle, 2慮.
- 25. The position of the diffraction peaks are determined by the distance between parallel planes of atoms. Braggs law calculates the angle where constructive interference from X-rays scattered by parallel planes of atoms will produce a diffraction peak. In most diffractometers, the X-ray wavelength l is fixed. Consequently, a family of planes produces a diffraction peak only at a specific angle 2q. dhkl is the vector drawn from the origin of the unit cell to intersect the crystallographic plane (hkl) at a 90属angle. dhkl, the vector magnitude, is the distance between parallel planes of atoms in the family (hkl) dhkl is a geometric function of the size and shape of the unit cell Braggs Law 了= 2dhkl
- 26. A Brief Introduction to Miller Indices The Miller indices (hkl) define the reciprocal axial intercepts of a plane of atoms with the unit cell The (hkl) plane of atoms intercepts the unit cell at a/, /, and / The (220) plane drawn to the right intercepts the unit cell at 遜a, 遜b, and does not intercept the c-axis. When a plane is parallel to an axis assumed to intercept at ; therefore its reciprocal is 0 The vector dhkl is drawn from the origin of the unit cell to intersect the crystallographic plane (hkl) at a 90属. The direction of dhkl is the crystallographic direction. The crystallographic direction is expressed using [] brackets, such as [220]
- 27. Braggs law provides a simplistic model to understand what conditions are required for diffraction. For parallel planes of atoms, with a space dhkl between the planes, constructive interference only occurs when Braggs law is satisfied. In our diffractometers, the X-ray wavelength l is fixed. Consequently, a family of planes produces a diffraction peak only at a specific angle 2q. Additionally, the plane normal [hkl] must be parallel to the diffraction vector s Plane normal [hkl]: the direction perpendicular to a plane of atoms Diffraction vector s: the vector that bisects the angle between the incident and diffracted beam Braggs Law 了= 2dhkl
- 28. Our powder diffractometers typically use the Bragg- Brentano geometry. The incident angle, w, is defined between the X-ray source and the sample. The diffraction angle, 2q, is defined between the incident beam and the detector. The incident angle w is always . of the detector angle 2q . In a q:2q instrument (e.g. Rigaku H3R), the tube is fixed, the sample rotates at q 属/min and the detector rotates at 2q 属/min. In a q:q instrument (e.g. PANalytical XPert Pro), the sample is fixed and the tube rotates at a rate q 属/min and the detector rotates at a rate of q 属/min.
- 29. A single crystal specimen in a Bragg-Brentano diffractometer would produce only one family of peaks in the diffraction pattern.
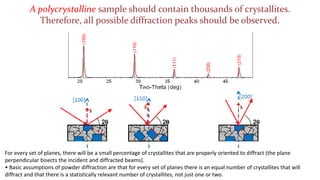
- 30. For every set of planes, there will be a small percentage of crystallites that are properly oriented to diffract (the plane perpendicular bisects the incident and diffracted beams). Basic assumptions of powder diffraction are that for every set of planes there is an equal number of crystallites that will diffract and that there is a statistically relevant number of crystallites, not just one or two. A polycrystalline sample should contain thousands of crystallites. Therefore, all possible diffraction peaks should be observed.
- 31. The spacing of one set of crystal planes in NaCl (table salt) is d = 0.282 nm. A monochromatic beam of X-rays produces a Bragg maximum when its glancing angle with these planes is = 7. Assuming that this is a first order maximum (n = 1), find the wavelength of the X-rays. The Bragg law is 2d sin = n了 了 = 2d sin = 2 (0.282 nm) sin 7 了 = 0.069 nm
- 32. 1. A beam of X-rays of wavelength 0.071 nm is diffracted by (110) plane of rock salt with lattice constant of 0.28 nm. Find the glancing angle for the second-order diffraction. Sol: Given data are: Wavelength (了) of X-rays = 0.071 nm Lattice constant (a) = 0.28 nm Plane (hkl) = (110) Order of diffraction = 2 Glancing angle 慮 = ? Braggs law is 2d sin 慮 = n了