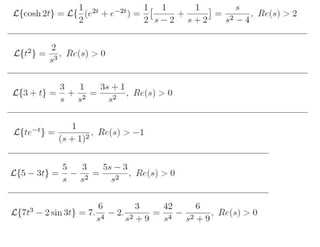Inverse Laplace Transform
Download as PPTX, PDF
0 likes364 views
This document discusses the inverse Laplace transform and how to calculate it using MATLAB. It defines the Laplace transform as an operator that takes a function of time, f(t), and transforms it into a function of complex frequency, F(s). It describes how to calculate the Laplace transform of a function in MATLAB by first defining the variables t and s as symbolic, then defining the function f(t) and using the laplace command. As an example, it calculates the Laplace transform of the function f(t) = -1.25 + 3.5te^-2t + 1.25e^-2t, getting the result F(s) = (s-5)/(s(s+2)^2).
Inverse Laplace Transform
- 1. Engineering Analysis Lab. - Inverse Laplace Transform Created by Omer W. Taha Computer Engineering Technique Third Stage
- 2. Definition The Laplace transform is a linear operator that switched a function f(t) to F(s). Go from time argument with real input to a complex angular frequency input which is complex.
- 5. Laplace Transforms with MATLAB a. Calculate the Laplace Transform using Matlab Calculating the Laplace F(s) transform of a function f(t) is quite simple in Matlab. First you need to specify that the variable t and s are symbolic ones. This is done with the command >> syms t s Next you define the function f(t). The actual command to calculate the transform is >> F=laplace(f,t,s) To make the expression more readable one can use the commands, simplify and pretty. here is an example for the function f(t), f (t) 1.25 3.5te2t 1.25e2t >> syms t s >> f=-1.25+3.5*t*exp(-2*t)+1.25*exp(-2*t); >> F=laplace(f,t,s) F = -5/4/s+7/2/(s+2)^2+5/4/(s+2) >> simplify(F) ans = (s-5)/s/(s+2)^2 >> pretty(ans) s - 5 ---------- 2 s (s + 2) which corresponds to F(s), s(s 2)2 ESE216 5 (s 5) F(s) Alternatively, one can write the function f(t) directly as part of the laplace command: >>F2=laplace(-1.25+3.5*t*exp(-2*t)+1.25*exp(-2*t))