分割时系列解析(滨罢厂)の入门
- 1. REQUIRE研究会:第31回 分割時系列解析の入門 2017/10/21 PM14:30 - @東京医科歯科大学 Koichiro Gibo, MD, MMSc(biostatistics)
- 2. はじめに ? 分割時系列解析(以下ITS: interrupted time-series)の入門編 です。 ? Bernal(2016)のチュートリアル論文が非常にわかりやすいの で、基本的にこの論文の内容にそって話を進めます。 ? また、この論文中に使われている、データやRスクリプトもサ プリメントからフリーで手に入ります。 ? https://academic.oup.com/ije/article/doi/10.1093/ije/dyw0 98/2622842/Interrupted-time-series-regression-for-the
- 3. 目次 1. はじめに (3min.) 2. ITSと因果とCounterfactual (7min.) 3. ITS総論 (15min.) 4. 各論:方法論的な問題点 (15min.)
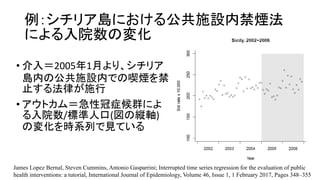
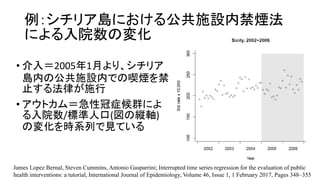
- 4. 例:シチリア島における公共施設内禁煙法 による入院数の変化 ? 介入=2005年1月より、シチリア 島内の公共施設内での喫煙を禁 止する法律が施行 ? アウトカム=急性冠症候群によ る入院数/標準人口(図の縦軸) の変化を時系列で見ている James Lopez Bernal, Steven Cummins, Antonio Gasparrini; Interrupted time series regression for the evaluation of public health interventions: a tutorial, International Journal of Epidemiology, Volume 46, Issue 1, 1 February 2017, Pages 348–355
- 5. ITS:interrupted time-series design ? このようにITSは、ある介入(禁煙法)の前後の時系列でアウ トカム(入院率)がどう変化するかを見るデザインである ? 一見非常に単純なデザインだが、Quasi-experimental design(準実験デザイン)の一つ。 ? うまくリサーチクエスチョンに合致すれば強力
- 6. 因果とは? ? 医学研究の目的は畢竟、原因と結果の関係(因果)を探ること。 ? Question: ? コーラを飲む(原因?介入) → ゲップが出る(結果):本当?
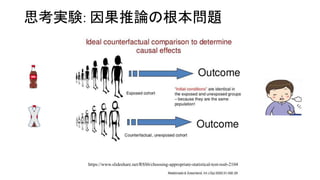
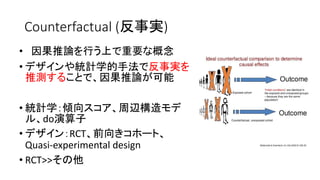
- 9. Counterfactual (反事実) ? 因果推論を行う上で重要な概念 ? デザインや統計学的手法で反事実を 推測することで、因果推論が可能 ? 統計学:傾向スコア、周辺構造モデ ル、do演算子 ? デザイン:RCT、前向きコホート、 Quasi-experimental design ? RCT>>その他
- 10. 目次 1. はじめに (3min.) 2. ITSと因果とCounterfactual (7min.) 3. ITS総論 (15min.) 4. 各論:方法論的な問題点 (15min.)
- 11. 例:シチリア島における公共施設内禁煙法 による入院数の変化 ? 介入=2005年1月より、シチリア 島内の公共施設内での喫煙を禁 止する法律が施行 ? アウトカム=急性冠症候群によ る入院数/標準人口(図の縦軸) の変化を時系列で見ている James Lopez Bernal, Steven Cummins, Antonio Gasparrini; Interrupted time series regression for the evaluation of public health interventions: a tutorial, International Journal of Epidemiology, Volume 46, Issue 1, 1 February 2017, Pages 348–355
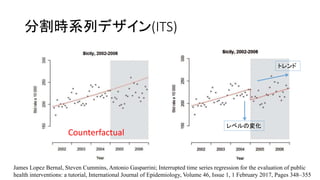
- 12. 分割時系列デザイン(ITS) Counterfactual James Lopez Bernal, Steven Cummins, Antonio Gasparrini; Interrupted time series regression for the evaluation of public health interventions: a tutorial, International Journal of Epidemiology, Volume 46, Issue 1, 1 February 2017, Pages 348–355 レベルの変化 トレンド
- 13. 分割時系列デザイン(ITS)の概要 ? 介入によるアウトカムへの影響(因果効果)を時系列のレベ ル変化(切片の変化)やトレンドの変化(傾きの変化)でみる 方法 ? 介入がなければ、そのまま時系列は変化しないままであっ ただろう(反事実)、という仮定部分と比較することで因果を 推測するデザイン ? 解析はsegmented regression + Poisson分布 で行うのが基本
- 14. ITSの前提条件 1. pre-intervation と post-intervation では集団の分布が変化 していない、つまり同じような背景をもっている集団である という仮定を置く 2. Pre-intervationの時系列変化が線形であるという仮定 3. 介入以外に時系列の変化を説明できるものがない Kontopantelis, Evangelos, et al. "Regression based quasi-experimental approach when randomisation is not an option: interrupted time series analysis." bmj 350 (2015): h2750.
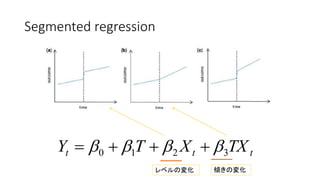
- 15. Segmented regression ttt TXXTY 3210 ???? ???? 傾きの変化レベルの変化
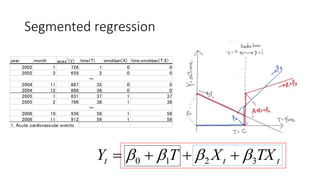
- 16. Segmented regression year month aces (Y) time(T) smokban(X) time:smokban(T:X) 2002 1 728 1 0 0 2002 2 659 2 0 0 ~ 2004 11 887 35 0 0 2004 12 886 36 0 0 2005 1 831 37 1 37 2005 2 796 38 1 38 ~ 2006 10 936 58 1 58 2006 11 912 59 1 59 1. Acute cardiovascular events 1 ttt TXXTY 3210 ???? ????
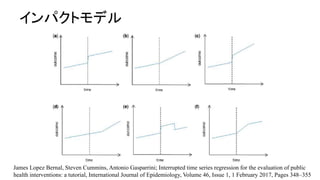
- 17. James Lopez Bernal, Steven Cummins, Antonio Gasparrini; Interrupted time series regression for the evaluation of public health interventions: a tutorial, International Journal of Epidemiology, Volume 46, Issue 1, 1 February 2017, Pages 348–355 インパクトモデル
- 18. インパクトモデル ? インパクトモデルの関数形はアプリオリに決定する。 ?例:法律の施行(介入)と入院数(アウトカム)との関係 ? 法律の制定によるアウトカムに対する効果は、制定後すぐに効 果が現れると期待される(レベルの変化あり)。 ?例:スマホアプリの導入(介入)とたらい回し件数(アウトカム) との関係 ? アプリの導入はすぐに効果は現れず(レベル変化なし)、口コミや 広報で徐々に効果が出て来ると考えられる(トレンドの変化あり) Katayama, Yusuke, et al. "Improvements in Patient Acceptance by Hospitals Following the Introduction of a Smartphone App for the Emergency Medical Service System: A Population-Based Before-and-After Observational Study in Osaka City, Japan." JMIR mHealth and uHealth 5.9 (2017).
- 19. タイムポイントの数 ? タイムポイントの数が多ければパワーも大きくなる。 ? 回帰分析を行う上で最小のタイムポイント数は? ? Pre とPostでそれぞれ8ポイントずつ(Penfold and Zhang, 2013) ? 多ければ多いほどいい? ? タイムポイントを細分化しすぎると、もともとITSの前提である観 察期間中の定常な共変量分布(年齢分布など)が外れ値など にviolateされやすくなるので注意 James Lopez Bernal, Steven Cummins, Antonio Gasparrini; Interrupted time series regression for the evaluation of public health interventions: a tutorial, International Journal of Epidemiology, Volume 46, Issue 1, 1 February 2017, Pages 348–355
- 20. アウトカム ? アウトカムは割合(率)なのかカウン ト(回数)なのか明確にする ? モデリングに影響する(後述) ? 天井効果?床効果に注意する ? 例えば測定するアウトカムの上限が 決まっている場合(たばこの本数をみ るときに2pack per dayが調査の上限 の場合など)は、その制約でトレンド が狭まってしまうかもしれない https://stats.stackexchange.com/questions/ 96715/what-criteria-must-be-met-in-order- to-conclude-a-ceiling-effect-is-occurring Jandoc, Racquel, et al. "Interrupted time series analysis in drug utilization research is increasing: systematic review and recommendations." Journal of clinical epidemiology 68.8 (2015): 950-956.
- 21. モデリング?推定方法 ? カウントデータ(回数)なので、基本的にはポアソン回帰モデル ? アウトカムが割合or率の場合にもポアソン回帰とオフセット項 で対応できる ? 以降のRスクリプトはBernal(2017)のsupplementより ? 例: ? model1 <- glm(aces ~ offset(log(stdpop)) + smokban + time, family=poisson, data) James Lopez Bernal, Steven Cummins, Antonio Gasparrini; Interrupted time series regression for the evaluation of public health interventions: a tutorial, International Journal of Epidemiology, Volume 46, Issue 1, 1 February 2017, Pages 348–355
- 22. おまけ:オフセット項って? ? ある時間t1とt2を考え、それぞれの時間でアウトカムがY1, Y2 回起きたとする。 ? 比較する集団の総数が変化する場合(n1, n2)はどうしたらよ いか? ? Y1/n1 と Y2/n2の比較?→1が上限なので単純な線形モデル では誤差分布に誤りが生じる ? ポアソン回帰ならオフセット項で解決できる。 TnYETnYE tttt 1010 )/][log()log(])[log( ???? ?????? オフセット項Yはポアソン 分布に従う 分布不明
- 23. 目次 1. はじめに (3min.) 2. ITSと因果とCounterfactual (7min.) 3. ITS総論 (15min.) 4. 各論:方法論的な問題点 (15min.)
- 24. 時系列データを回帰分析で行うときの問題 ? 方法論的には以下のような問題が発生する 1. 過分散 (over-dispersion) 2. 周期性 (seasonality) 3. 時間依存性変数(time dependent variables) 4. 自己相関 (autocorrelation) James Lopez Bernal, Steven Cummins, Antonio Gasparrini; Interrupted time series regression for the evaluation of public health interventions: a tutorial, International Journal of Epidemiology, Volume 46, Issue 1, 1 February 2017, Pages 348–355
- 25. 過分散(over-dispersion)の問題 ? ポアソン分布はまれな事象ではよく当てはまるがそうでない場 合は分散を過剰推定してしまう傾向にあることが知られる。 ? その場合は負の2項分布や分布の仮定が不要な擬似尤度を 使った推定をする ? summary(model1)$dispersion #1.5以上なら過分散あり ? model2.1 <- glm(aces ~ offset(log(stdpop)) + smokban + time, family=quasipoisson,data) #擬似尤度回帰 ? model2.2 <- MASS::glm.nb(aces ~ offset(log(stdpop)) + smokban + time, data) #負の二項分布回帰
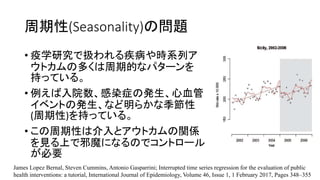
- 26. 周期性(Seasonality)の問題 ? 疫学研究で扱われる疾病や時系列ア ウトカムの多くは周期的なパターンを 持っている。 ? 例えば入院数、感染症の発生、心血管 イベントの発生、など明らかな季節性 (周期性)を持っている。 ? この周期性は介入とアウトカムの関係 を見る上で邪魔になるのでコントロール が必要 James Lopez Bernal, Steven Cummins, Antonio Gasparrini; Interrupted time series regression for the evaluation of public health interventions: a tutorial, International Journal of Epidemiology, Volume 46, Issue 1, 1 February 2017, Pages 348–355
- 27. 周期性の問題:解決策①ダミー共変量 ? 最もシンプルな解決策。例えばmonthsをそれぞれダミー変 数化して共変量としてモデルに組み込む。 ? 2値の共変量がいっぱい入るので時系列グラフとしては階段 状の折れ線グラフになる("まとめ"参照) ? Cons: モデルパラメーターが多くなり推定精度が落ちる可能 性、隣接する時間点同士の生物学的にあり得ない飛躍が起 きる可能性 Bhaskaran, Krishnan, et al. "Time series regression studies in environmental epidemiology." International journal of epidemiology 42.4 (2013): 1187-1195.
- 28. 周期性の問題:解決策②フーリエ級数 ? フーリエ級数って? ? 複雑な周期関数を単純な形の周期性を持つ関数 (ex: sine/cosine)の和に表現したもの ? Rではharmonic項を入れる。(一般フーリエ級数 の波動部分がハーモニック項) ? 参考:http://www.di.fc.ul.pt/~jpn/r/fourier/fourier.html ? model3 <- glm(aces ~ offset(log(stdpop)) + smokban + time + harmonic(month,2,12), family=poisson, data)
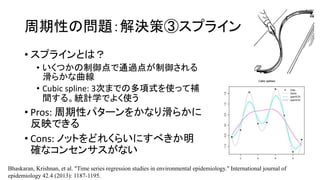
- 29. 周期性の問題:解決策③スプライン ? スプラインとは? ? いくつかの制御点で通過点が制御される 滑らかな曲線 ? Cubic spline: 3次までの多項式を使って補 間する。統計学でよく使う ? Pros: 周期性パターンをかなり滑らかに 反映できる ? Cons: ノットをどれくらいにすべきか明 確なコンセンサスがない Bhaskaran, Krishnan, et al. "Time series regression studies in environmental epidemiology." International journal of epidemiology 42.4 (2013): 1187-1195.
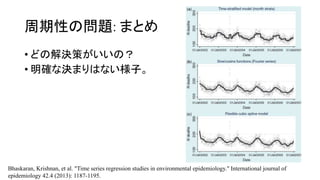
- 30. 周期性の問題: まとめ ? どの解決策がいいの? ? 明確な決まりはない様子。 Bhaskaran, Krishnan, et al. "Time series regression studies in environmental epidemiology." International journal of epidemiology 42.4 (2013): 1187-1195.
- 31. 時間依存性変数の問題 ? ITSの強みの一つは典型的な時間依存性変数(年齢etc)の 影響を受けにくいことにある ? 年齢や社会経済的ステータスの分布は時間経過に対しゆっくり変 化していくので、影響を与えにくいとかんがえられる ? 感染症のアウトブレイクや気候の変化などの急速な変化を もたらす時間依存性変数は調整が必要→通常回帰モデル に共変量投入することができる ? 広義には、周期性も時間依存性変数に含まれる James Lopez Bernal, Steven Cummins, Antonio Gasparrini; Interrupted time series regression for the evaluation of public health interventions: a tutorial, International Journal of Epidemiology, Volume 46, Issue 1, 1 February 2017, Pages 348–355
- 32. 自己相関の問題 ? 分断時系列解析に限らず、時系列解析に必ずついて回る 問題。 ? 例えば、株価の将来の予測をする時に、前日もしくは数日 前の株価が明日の株価に影響する、ということが容易に想 像がつくだろう。 ? このように過去の時系列自身に影響されることを自己相関 (autocorrelation)と呼ぶ ? 自己相関があると回帰モデルにおける最も強い仮定の一つ である、独立性の仮定を損ねることになる
- 33. 自己相関の問題: Pros and Cons ? 疫学研究においては、周期性さえ顧慮されていれば自己相 関はあまり問題にならないとする論文もあるし、考慮すべき という論文もある。(下記1, 2) ? コンセンサス: ? 同じ集団を追跡するなら、必ず考慮する ? 周期性を調整したあとのモデルで、自己相関の有無はチェックして おく 2. James Lopez Bernal, Steven Cummins, Antonio Gasparrini; Interrupted time series regression for the evaluation of public health interventions: a tutorial, International Journal of Epidemiology, Volume 46, Issue 1, 1 February 2017, Pages 348–355 1. Jandoc, Racquel, et al. "Interrupted time series analysis in drug utilization research is increasing: systematic review and recommendations." Journal of clinical epidemiology 68.8 (2015): 950-956.
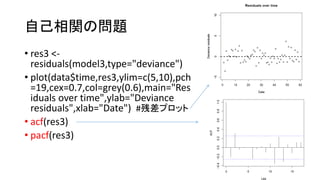
- 34. 自己相関の問題 ? res3 <- residuals(model3,type="deviance") ? plot(data$time,res3,ylim=c(5,10),pch =19,cex=0.7,col=grey(0.6),main="Res iduals over time",ylab="Deviance residuals",xlab="Date") #残差プロット ? acf(res3) ? pacf(res3)
- 35. 結語 ? 時系列データを用いて、政策?プラクティスのシステマティッ クな変化を介入として、アウトカムがどう変化するかをみる 研究デザインが分割時系列デザイン(ITS) ? ITSの前提条件が満たされるならば、かなり強力に因果の推 定が可能→準実験デザイン(Quasi-experimental) ? 散布図を書く ? インパクトモデルを立てる ? 解析の基礎:segmented regression + Poisson distribution ? 各論の問題点をクリアする
- 36. 参考文献 ? Bernal, J. L., Cummins, S., & Gasparrini, A. (2017). Interrupted time series regression for the evaluation of public health interventions: a tutorial. International journal of epidemiology, 46(1), 348-355. ? Bhaskaran, Krishnan, et al. "Time series regression studies in environmental epidemiology." International journal of epidemiology 42.4 (2013): 1187-1195. ? Jandoc, Racquel, et al. "Interrupted time series analysis in drug utilization research is increasing: systematic review and recommendations." Journal of clinical epidemiology 68.8 (2015): 950- 956.
- 37. 参考文献 ? Kontopantelis, Evangelos, et al. "Regression based quasi-experimental approach when randomisation is not an option: interrupted time series analysis." bmj 350 (2015): h2750. ? Katayama, Yusuke, et al. "Improvements in Patient Acceptance by Hospitals Following the Introduction of a Smartphone App for the Emergency Medical Service System: A Population-Based Before-and- After Observational Study in Osaka City, Japan." JMIR mHealth and uHealth 5.9 (2017). ? Penfold, Robert B., and Fang Zhang. "Use of interrupted time series analysis in evaluating health care quality improvements." Academic pediatrics 13.6 (2013): S38-S44.













![おまけ:オフセット項って?
? ある時間t1とt2を考え、それぞれの時間でアウトカムがY1, Y2
回起きたとする。
? 比較する集団の総数が変化する場合(n1, n2)はどうしたらよ
いか?
? Y1/n1 と Y2/n2の比較?→1が上限なので単純な線形モデル
では誤差分布に誤りが生じる
? ポアソン回帰ならオフセット項で解決できる。
TnYETnYE tttt 1010 )/][log()log(])[log( ???? ??????
オフセット項Yはポアソン
分布に従う
分布不明](https://image.slidesharecdn.com/random-171022095026/85/ITS-22-320.jpg)