Jabina
Download as DOCX, PDF0 likes195 views
The document discusses decision making under certainty. It provides examples of decisions under certainty, such as purchasing food, versus decisions not under certainty, like choosing investments. It describes two methods for making decisions under certainty with multiple criteria: the cutoff screening method, which eliminates choices that don't meet cutoff criteria, and the weighted sum method, which assigns weights and ratings to criteria to calculate a weighted sum for each choice.
1 of 2
Download to read offline


Recommended
Create a Powerful B2B Sales Machine - Part 2



Create a Powerful B2B Sales Machine - Part 2Fusion Marketing Partners
╠²
Create a powerful B2B sales machine by reviewing and practicing these 8 keys for success
1. Make sure there is complete alignment between the marketing and sales departments.
2. Concentrate your efforts on finding the companies and individuals that have a genuine need for what you offer.
3. Never lose a deal alone.
4. Keep things simple and focused on as few priorities as possible.
LetŌĆÖs now cover the final four keys, beginning with treating B2B sales leads with care and respect. It really offends me when sales departments mishandle the leads/inquiries given to them by the marketing department. I have seen sales reps ignore leads, denigrate leads, and follow them up in a half-hearted manner. Often this occurs because the VP of Sales speaks poorly about what marketing is doing, creating a culture where reps feel it is okay not to work the leads they are given.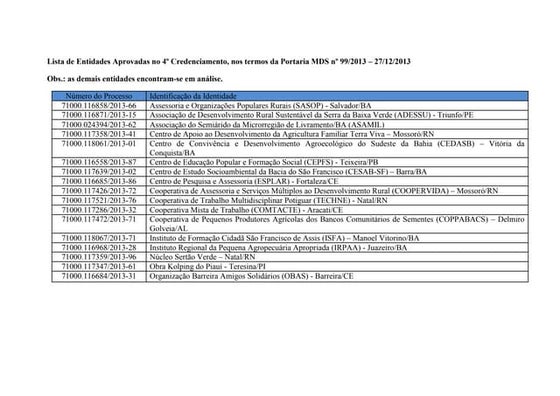

Lista de entidades aprovadas no 4┬║ credenciamento nos termos da portaria mds ...Secretaria Especial do Desenvolvimento Social
╠²
Este documento lista 16 entidades que foram aprovadas no 4o Credenciamento de acordo com a Portaria MDS no 99/2013. As entidades aprovadas incluem associa├¦├Ąes rurais, cooperativas, institutos e organiza├¦├Ąes que apoiam o desenvolvimento sustent├Īvel de comunidades no Nordeste e Centro-Oeste do Brasil.Contoh narrative text



Contoh narrative textOperator Warnet Vast Raha
╠²
The document contains several examples of different types of Indonesian text structures, including narratives, descriptions, procedures, explanations, expositions, and reports. The narrative text describes a legend about two animals, Sura the shark and Baya the crocodile, who fight over food but eventually agree to live separately. The descriptive text provides details about American singer and actress Miley Cyrus. The procedure text outlines the steps to operate a fan. The explanation text defines and describes tsunamis.Diplomkomat - z├Īv─øre─Źn├Ī prezentace na SIC 2013



Diplomkomat - z├Īv─øre─Źn├Ī prezentace na SIC 2013Inovace Pro Spole─Źnost
╠²
STOP diplomk├Īm do ┼Īupl├Łku!
Najdi praktick├® t├®ma pro svoji z├Īv─øre─Źnou pr├Īci a p┼Öehledn├Į seznam zad├Īn├Ł od firem, startup┼» a neziskovek.
V├Łce na: https://www.facebook.com/diplomkomat Social media and employee privacy



Social media and employee privacyDenisa Dobrin
╠²
This document presents information on social media and employee privacy. It includes an introduction, definitions of social media and discussions of the differences between social and business uses. The main concerns addressed are legal liability, legal compliance, productivity, security and employee rights. It notes that privacy in the workplace is limited and companies have real concerns about liability and productivity that lead to social media policies. The conclusion states that this is an uncharted territory that companies must learn to navigate amidst changing social media and privacy issues.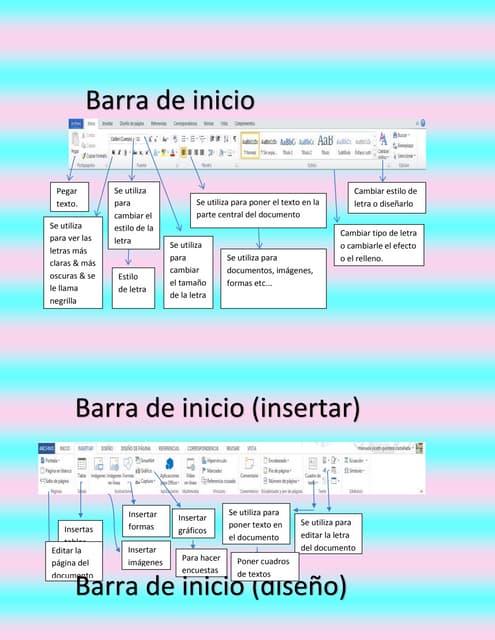

Barra de inicioManuela yiceth
╠²
Este documento describe las diferentes herramientas y funciones disponibles en Microsoft Word para editar texto, insertar elementos como im├Īgenes y tablas, cambiar el formato y estilo de la letra, dise├▒ar p├Īginas e insertar gr├Īficos y encuestas. Se mencionan opciones como cambiar el tama├▒o y tipo de letra, usar negrita, alinear texto, pegar contenido, insertar formas, tablas e im├Īgenes, y editar m├Īrgenes, columnas y el tama├▒o de p├Īgina.Strategic Plays for the 2nd Half of Market Recovery: Detroit



Strategic Plays for the 2nd Half of Market Recovery: DetroitEDR
╠²
This document summarizes a presentation on strategic plays for the commercial real estate market recovery in the second half of 2013 and 2014. It notes that market fundamentals are improving, with increasing transaction volumes, lending, and CMBS issuance activity across various property types and market sizes. It highlights opportunities in target industries like private equity, foreign investors, and growing lenders. It recommends leveraging technology to improve efficiency and using education to establish expertise in areas like the new ASTM standards. The presentation provides an overview of improving conditions and strategic recommendations to capitalize on opportunities in the recovering commercial real estate market.Microeconomics For Today 9th Edition Tucker Solutions Manual



Microeconomics For Today 9th Edition Tucker Solutions Manualbodaniwshiar
╠²
Microeconomics For Today 9th Edition Tucker Solutions Manual
Microeconomics For Today 9th Edition Tucker Solutions Manual
Microeconomics For Today 9th Edition Tucker Solutions Manual102 Creating Value with Real Options



102 Creating Value with Real Optionsmjvandenplas
╠²
This deck demonstrates how asset value can be created where it had not existed before. We create asset value through the construction of a ŌĆ£Real Option.ŌĆØ
ŌĆ£Real OptionŌĆØ thinking was in vogue during the 80ŌĆÖs but fell out of favor for lack of calculating tools. Now that we have the proper computer tools, ŌĆ£Real OptionŌĆØ thinking should be brought back in.
In this deck, we create $4.5 million dollars ŌĆ£Real OptionŌĆØ value through strategic thinking, with the assistance of a Bayesian revision, by examining a classic example, the Wildcatter Oil-Drill or Not question.
Decision Tree- M.B.A -DecSci



Decision Tree- M.B.A -DecSciLesly Lising
╠²
The document discusses decision trees, which are diagrams that illustrate decisions and their potential consequences. It provides examples of decision trees used by two companies - Manly Plastics and Vine Desserts - to analyze decisions about new product development and business location selection. It also discusses key concepts in decision trees, including decision nodes, chance nodes, expected value calculations, and how decision trees can be used for regression and survival analysis involving continuous or time-to-event outcomes.Decision theory



Decision theoryAditya Mahagaonkar
╠²
The document discusses decision theory and decision trees. It introduces decision making under certainty, risk, and uncertainty. It defines elements related to decisions like goals, courses of action, states of nature, and payoffs. It also discusses concepts like expected monetary value, expected profit with perfect information, expected value of perfect information, and expected opportunity loss. Examples are provided to demonstrate calculating these metrics. Finally, it provides an overview of how to construct a decision tree, including defining the different node types and how to calculate values within the tree.Decision Theory



Decision TheoryOsama Manzoor
╠²
Decision theory ,Operations Research, Decision Trees, Optimistic Approach , Conservative Approach , Maximax ,Minimax , Decision Theory LEARNING OBJECTIVES SUPPLEMENT OUTLINE 5S.5.docx



Decision Theory LEARNING OBJECTIVES SUPPLEMENT OUTLINE 5S.5.docxsimonithomas47935
╠²
Decision Theory
LEARNING OBJECTIVES SUPPLEMENT OUTLINE 5S.5 Decision Making under Uncertainty, 219
After completing this supplement, you 5S.6 Decision Making under Risk, 220 5S.1 Introduction, 216
should be able to: 5S.7 Decision Trees, 2215S.2 The Decision Process and Causes of
L05S.1 Outline the steps in the decision Poor Decisions, 217 5S.8 Expected Value of Perfect
process. Information, 2235S.3 Decision Environments, 218
L05S.2 Name some causes of poor 5S.9 Sensitivity Analysis, 224
decisions. 5S.4 Decision Making under Certainty, 218
L05S.3 Describe and use techniques that
apply to decision making under
uncertainty.
L05S.4 Describe and use the expected-
value approach.
L05S.5 Construct a decision tree and use
it to analyze a problem.
L05S.6 Compute the expected value of
perfect information.
L05S.7 Conduct sensitivity analysis on a
simple decision problem.
55.1 INTRODUCTION
-
Decision theory represents a general approach to decision making. It is suitable for a wide
range of operations management decisions. Among them are capacity planning, product and
service design, equipment selection, and location planning. Decisions that lend themselves to
a decision theory approach tend to be characterized by the following elements:
1. A set of possible future conditions that will have a bearing on the results of the decision.
2. A list of alternatives for the manager to choose from.
3. A known payoff for each alternative under each possible future condition.
To use this approach, a decision maker would employ this process:
1. Identify the possible future conditions (e.g., demand will be low, medium, or high; the
competitor will or will not introduce a new product). These are called states of nature.
2. Develop a list of possible alternatives, one of which may be to do nothing.
t
3. Determine or estimate the payoff associated with each alternative for every possible
future condition.
---- ----------------------------------------~--
216
217 Supplement to Chapter Five Decision Theory
If possible, estimate the likelihood of each possible future condition.
5. Evaluate alternatives according to some decision criterion (e.g., maximize expected
profit), and select the best alternative.
The information for a decision is often summarized in a payoff table, which shows the
expected payoffs for each alternative under the various possible states of nature. These tables
are helpful in choosing among alternatives because they facilitate comparison of alternatives.
Consider the following payoff table, which illustrates a capacity planning problem.
POSSIBLE FUTURE DEMAND
Alternatives Low Moderate High
Small facility $10* $10 $10
Medium facility 7 12 12
Large facil ity (4) 2 16
'Present value in $ millions.
The payoffs are shown in the body of the table. In this instance, the payoffs are in terms
of present values, which represent equivalent current dollar values of expected .Decision Theory LEARNING OBJECTIVES SUPPLEMENT OUTLINE 5S..docx



Decision Theory LEARNING OBJECTIVES SUPPLEMENT OUTLINE 5S..docxtheodorelove43763
╠²
Decision Theory
LEARNING OBJECTIVES SUPPLEMENT OUTLINE 5S.5 Decision Making under Uncertainty, 219
After completing this supplement, you 5S.6 Decision Making under Risk, 220 5S.1 Introduction, 216
should be able to: 5S.7 Decision Trees, 2215S.2 The Decision Process and Causes of
L05S.1 Outline the steps in the decision Poor Decisions, 217 5S.8 Expected Value of Perfect
process. Information, 2235S.3 Decision Environments, 218
L05S.2 Name some causes of poor 5S.9 Sensitivity Analysis, 224
decisions. 5S.4 Decision Making under Certainty, 218
L05S.3 Describe and use techniques that
apply to decision making under
uncertainty.
L05S.4 Describe and use the expected-
value approach.
L05S.5 Construct a decision tree and use
it to analyze a problem.
L05S.6 Compute the expected value of
perfect information.
L05S.7 Conduct sensitivity analysis on a
simple decision problem.
55.1 INTRODUCTION
-
Decision theory represents a general approach to decision making. It is suitable for a wide
range of operations management decisions. Among them are capacity planning, product and
service design, equipment selection, and location planning. Decisions that lend themselves to
a decision theory approach tend to be characterized by the following elements:
1. A set of possible future conditions that will have a bearing on the results of the decision.
2. A list of alternatives for the manager to choose from.
3. A known payoff for each alternative under each possible future condition.
To use this approach, a decision maker would employ this process:
1. Identify the possible future conditions (e.g., demand will be low, medium, or high; the
competitor will or will not introduce a new product). These are called states of nature.
2. Develop a list of possible alternatives, one of which may be to do nothing.
t
3. Determine or estimate the payoff associated with each alternative for every possible
future condition.
---- ----------------------------------------~--
216
217 Supplement to Chapter Five Decision Theory
If possible, estimate the likelihood of each possible future condition.
5. Evaluate alternatives according to some decision criterion (e.g., maximize expected
profit), and select the best alternative.
The information for a decision is often summarized in a payoff table, which shows the
expected payoffs for each alternative under the various possible states of nature. These tables
are helpful in choosing among alternatives because they facilitate comparison of alternatives.
Consider the following payoff table, which illustrates a capacity planning problem.
POSSIBLE FUTURE DEMAND
Alternatives Low Moderate High
Small facility $10* $10 $10
Medium facility 7 12 12
Large facil ity (4) 2 16
'Present value in $ millions.
The payoffs are shown in the body of the table. In this instance, the payoffs are in terms
of present values, which represent equivalent current dollar values of expected future income.165662191 chapter-03-answers-1



165662191 chapter-03-answers-1Firas Husseini
╠²
This document provides 10 teaching suggestions for instructors to help students better understand key concepts in decision analysis. Suggestions include having students describe personal decisions they made and which steps of the decision-making process they used; role playing to define problems and alternatives; discussing types of decisions under certainty, risk, and uncertainty; and using decision trees and Bayesian analysis to solve problems. The goal is for students to recognize how decision theory applies to important real-life decisions. Alternative examples provided apply concepts like expected monetary value to problems involving purchasing industrial robots.165662191 chapter-03-answers-1



165662191 chapter-03-answers-1BookStoreLib
╠²
This document provides 10 teaching suggestions for instructors to help students better understand key concepts in decision analysis. Suggestions include having students describe personal decisions they made and which steps of the decision-making process they used; role playing to define problems and alternatives; discussing decision types like certainty, risk, and uncertainty; and using decision trees to analyze large, complex problems by breaking them into smaller parts. The document also provides two alternative examples applying decision analysis concepts to a case study about a business owner deciding whether to purchase industrial robots.Decision analysis



Decision analysisYoung Alista
╠²
The document describes decision analysis and provides examples of how decision trees and tables can be used to capture complex decision-making processes. It discusses five parts of a decision-making model: identify the problem, formulate options, model the problem, analyze the model, and implement and test the solution. Anchoring and framing errors in judgment are explained with examples. Finally, the use of decision trees and tables is demonstrated on examples involving business policies and rules.Decision analysis



Decision analysisHarry Potter
╠²
The document describes decision analysis and decision making. It discusses identifying the problem, formulating a model, analyzing the model, testing results, and implementing solutions. It also discusses anchoring and framing biases that can influence decisions. Anchoring occurs when a trivial factor serves as a starting point for estimates. Framing affects how alternatives are perceived in terms of wins and losses. The way a problem is framed can influence choices. Decision trees and tables are described as ways to represent complex decisions involving multiple conditions. Creating decision models allows for a more rigorous analysis of problems compared to using narratives alone.Decision analysis



Decision analysisLuis Goldster
╠²
The document describes decision analysis and decision making. It discusses identifying the problem, formulating a model, analyzing the model, testing results, and implementing solutions. It also discusses anchoring and framing biases that can influence decisions. Anchoring occurs when a trivial factor serves as a starting point for estimates. Framing affects how alternatives are perceived in terms of wins and losses. The way a problem is framed can influence choices made. Decision trees and tables are described as ways to represent complex decisions and business logic involving multiple conditions. Creating decision models allows for a more rigorous analysis of problems compared to using only narrative descriptions.Decision analysis



Decision analysisFraboni Ec
╠²
The document describes decision analysis and decision making. It discusses identifying the problem, formulating a model, analyzing the model, testing results, and implementing solutions. It also discusses sources of errors like anchoring and framing biases. Anchoring occurs when people rely too heavily on the first piece of information when making decisions. Framing refers to how the options are presented, which can influence choices. The document provides examples to illustrate these concepts and emphasizes the importance of focusing on the consequences of choices rather than how problems are framed.Decision analysis



Decision analysisTony Nguyen
╠²
The document describes decision analysis and provides examples of how decision trees and tables can be used to analyze complex decisions. It discusses five parts of a decision-making model: identify the problem, formulate options, model the problem, analyze the model, and implement and test the solution. Anchoring and framing errors in judgment are described. Examples are provided to illustrate anchoring biases and how framing a problem as a sure win versus sure loss can influence choices. The use of decision trees to represent sequential decisions and incorporate uncertainty is demonstrated. Creating decision tables to systematically capture complex business rules is also illustrated.Decision analysis



Decision analysisJames Wong
╠²
The document describes decision analysis and decision making. It discusses identifying the problem, formulating a model, analyzing the model, testing results, and implementing solutions. It also discusses anchoring and framing biases that can influence decisions. Anchoring occurs when people rely too heavily on an irrelevant starting value. Framing means how a decision is perceived, such as in terms of gains or losses, can influence choices. The document provides an example where how a coin flip problem is framed affects whether people prefer a sure outcome or chance of gain/loss. Effective decision making requires understanding values, objectives, uncertainties, and consequences of options.Lecture 4: NBERMetrics



Lecture 4: NBERMetricsNBER
╠²
This document summarizes a lecture on using moment inequalities to estimate preference parameters from discrete choice models. It discusses how this approach differs from standard empirical models by working directly with the inequalities that define optimal behavior. The approach assumes the utility from the actual choice should be larger than the utility from a considered but discarded counterfactual choice. Parameter values that satisfy these inequalities on average are accepted. The document then provides a single agent example to illustrate this approach.Making Decisions Presentation



Making Decisions Presentationandyped
╠²
This document discusses different approaches to decision making including certainty, uncertainty, and risk. It begins with an outline of the chapter which describes how managers need structure to make decisions in complex conditions. It then covers decision making with certainty, uncertainty using criteria like Laplace, Wald, and Savage, risk using expected values, and sequential decisions using decision trees. Limitations of the criteria are noted.Questions To Ask An Optimization Vendor



Questions To Ask An Optimization Vendorsourcingdoctor
╠²
Trying to find the right strategic sourcing decision optimization solution can be very confusing. Asking the right questions will go a long way towards finding the right solution.MBA 623_Decision Theory presentation for masters degree class.pptx



MBA 623_Decision Theory presentation for masters degree class.pptxjcsan1992
╠²
masteral subject for operations managementChristian decision making



Christian decision makingChristian Tobing
╠²
This document discusses different approaches to decision making under uncertainty, including maximin, expected monetary value, and multi-attribute utility analysis. It explains that maximin is inherently pessimistic by only considering the worst possible outcome for each option. Expected monetary value focuses only on monetary attributes and assumes a linear value function for money. Multi-attribute utility analysis derives single-attribute utility functions and combines them to evaluate options based on multiple attributes like time, cost, and risk preferences. It can incorporate non-monetary attributes if preferences conform to specific axioms.More Related Content
Similar to Jabina (20)
Microeconomics For Today 9th Edition Tucker Solutions Manual



Microeconomics For Today 9th Edition Tucker Solutions Manualbodaniwshiar
╠²
Microeconomics For Today 9th Edition Tucker Solutions Manual
Microeconomics For Today 9th Edition Tucker Solutions Manual
Microeconomics For Today 9th Edition Tucker Solutions Manual102 Creating Value with Real Options



102 Creating Value with Real Optionsmjvandenplas
╠²
This deck demonstrates how asset value can be created where it had not existed before. We create asset value through the construction of a ŌĆ£Real Option.ŌĆØ
ŌĆ£Real OptionŌĆØ thinking was in vogue during the 80ŌĆÖs but fell out of favor for lack of calculating tools. Now that we have the proper computer tools, ŌĆ£Real OptionŌĆØ thinking should be brought back in.
In this deck, we create $4.5 million dollars ŌĆ£Real OptionŌĆØ value through strategic thinking, with the assistance of a Bayesian revision, by examining a classic example, the Wildcatter Oil-Drill or Not question.
Decision Tree- M.B.A -DecSci



Decision Tree- M.B.A -DecSciLesly Lising
╠²
The document discusses decision trees, which are diagrams that illustrate decisions and their potential consequences. It provides examples of decision trees used by two companies - Manly Plastics and Vine Desserts - to analyze decisions about new product development and business location selection. It also discusses key concepts in decision trees, including decision nodes, chance nodes, expected value calculations, and how decision trees can be used for regression and survival analysis involving continuous or time-to-event outcomes.Decision theory



Decision theoryAditya Mahagaonkar
╠²
The document discusses decision theory and decision trees. It introduces decision making under certainty, risk, and uncertainty. It defines elements related to decisions like goals, courses of action, states of nature, and payoffs. It also discusses concepts like expected monetary value, expected profit with perfect information, expected value of perfect information, and expected opportunity loss. Examples are provided to demonstrate calculating these metrics. Finally, it provides an overview of how to construct a decision tree, including defining the different node types and how to calculate values within the tree.Decision Theory



Decision TheoryOsama Manzoor
╠²
Decision theory ,Operations Research, Decision Trees, Optimistic Approach , Conservative Approach , Maximax ,Minimax , Decision Theory LEARNING OBJECTIVES SUPPLEMENT OUTLINE 5S.5.docx



Decision Theory LEARNING OBJECTIVES SUPPLEMENT OUTLINE 5S.5.docxsimonithomas47935
╠²
Decision Theory
LEARNING OBJECTIVES SUPPLEMENT OUTLINE 5S.5 Decision Making under Uncertainty, 219
After completing this supplement, you 5S.6 Decision Making under Risk, 220 5S.1 Introduction, 216
should be able to: 5S.7 Decision Trees, 2215S.2 The Decision Process and Causes of
L05S.1 Outline the steps in the decision Poor Decisions, 217 5S.8 Expected Value of Perfect
process. Information, 2235S.3 Decision Environments, 218
L05S.2 Name some causes of poor 5S.9 Sensitivity Analysis, 224
decisions. 5S.4 Decision Making under Certainty, 218
L05S.3 Describe and use techniques that
apply to decision making under
uncertainty.
L05S.4 Describe and use the expected-
value approach.
L05S.5 Construct a decision tree and use
it to analyze a problem.
L05S.6 Compute the expected value of
perfect information.
L05S.7 Conduct sensitivity analysis on a
simple decision problem.
55.1 INTRODUCTION
-
Decision theory represents a general approach to decision making. It is suitable for a wide
range of operations management decisions. Among them are capacity planning, product and
service design, equipment selection, and location planning. Decisions that lend themselves to
a decision theory approach tend to be characterized by the following elements:
1. A set of possible future conditions that will have a bearing on the results of the decision.
2. A list of alternatives for the manager to choose from.
3. A known payoff for each alternative under each possible future condition.
To use this approach, a decision maker would employ this process:
1. Identify the possible future conditions (e.g., demand will be low, medium, or high; the
competitor will or will not introduce a new product). These are called states of nature.
2. Develop a list of possible alternatives, one of which may be to do nothing.
t
3. Determine or estimate the payoff associated with each alternative for every possible
future condition.
---- ----------------------------------------~--
216
217 Supplement to Chapter Five Decision Theory
If possible, estimate the likelihood of each possible future condition.
5. Evaluate alternatives according to some decision criterion (e.g., maximize expected
profit), and select the best alternative.
The information for a decision is often summarized in a payoff table, which shows the
expected payoffs for each alternative under the various possible states of nature. These tables
are helpful in choosing among alternatives because they facilitate comparison of alternatives.
Consider the following payoff table, which illustrates a capacity planning problem.
POSSIBLE FUTURE DEMAND
Alternatives Low Moderate High
Small facility $10* $10 $10
Medium facility 7 12 12
Large facil ity (4) 2 16
'Present value in $ millions.
The payoffs are shown in the body of the table. In this instance, the payoffs are in terms
of present values, which represent equivalent current dollar values of expected .Decision Theory LEARNING OBJECTIVES SUPPLEMENT OUTLINE 5S..docx



Decision Theory LEARNING OBJECTIVES SUPPLEMENT OUTLINE 5S..docxtheodorelove43763
╠²
Decision Theory
LEARNING OBJECTIVES SUPPLEMENT OUTLINE 5S.5 Decision Making under Uncertainty, 219
After completing this supplement, you 5S.6 Decision Making under Risk, 220 5S.1 Introduction, 216
should be able to: 5S.7 Decision Trees, 2215S.2 The Decision Process and Causes of
L05S.1 Outline the steps in the decision Poor Decisions, 217 5S.8 Expected Value of Perfect
process. Information, 2235S.3 Decision Environments, 218
L05S.2 Name some causes of poor 5S.9 Sensitivity Analysis, 224
decisions. 5S.4 Decision Making under Certainty, 218
L05S.3 Describe and use techniques that
apply to decision making under
uncertainty.
L05S.4 Describe and use the expected-
value approach.
L05S.5 Construct a decision tree and use
it to analyze a problem.
L05S.6 Compute the expected value of
perfect information.
L05S.7 Conduct sensitivity analysis on a
simple decision problem.
55.1 INTRODUCTION
-
Decision theory represents a general approach to decision making. It is suitable for a wide
range of operations management decisions. Among them are capacity planning, product and
service design, equipment selection, and location planning. Decisions that lend themselves to
a decision theory approach tend to be characterized by the following elements:
1. A set of possible future conditions that will have a bearing on the results of the decision.
2. A list of alternatives for the manager to choose from.
3. A known payoff for each alternative under each possible future condition.
To use this approach, a decision maker would employ this process:
1. Identify the possible future conditions (e.g., demand will be low, medium, or high; the
competitor will or will not introduce a new product). These are called states of nature.
2. Develop a list of possible alternatives, one of which may be to do nothing.
t
3. Determine or estimate the payoff associated with each alternative for every possible
future condition.
---- ----------------------------------------~--
216
217 Supplement to Chapter Five Decision Theory
If possible, estimate the likelihood of each possible future condition.
5. Evaluate alternatives according to some decision criterion (e.g., maximize expected
profit), and select the best alternative.
The information for a decision is often summarized in a payoff table, which shows the
expected payoffs for each alternative under the various possible states of nature. These tables
are helpful in choosing among alternatives because they facilitate comparison of alternatives.
Consider the following payoff table, which illustrates a capacity planning problem.
POSSIBLE FUTURE DEMAND
Alternatives Low Moderate High
Small facility $10* $10 $10
Medium facility 7 12 12
Large facil ity (4) 2 16
'Present value in $ millions.
The payoffs are shown in the body of the table. In this instance, the payoffs are in terms
of present values, which represent equivalent current dollar values of expected future income.165662191 chapter-03-answers-1



165662191 chapter-03-answers-1Firas Husseini
╠²
This document provides 10 teaching suggestions for instructors to help students better understand key concepts in decision analysis. Suggestions include having students describe personal decisions they made and which steps of the decision-making process they used; role playing to define problems and alternatives; discussing types of decisions under certainty, risk, and uncertainty; and using decision trees and Bayesian analysis to solve problems. The goal is for students to recognize how decision theory applies to important real-life decisions. Alternative examples provided apply concepts like expected monetary value to problems involving purchasing industrial robots.165662191 chapter-03-answers-1



165662191 chapter-03-answers-1BookStoreLib
╠²
This document provides 10 teaching suggestions for instructors to help students better understand key concepts in decision analysis. Suggestions include having students describe personal decisions they made and which steps of the decision-making process they used; role playing to define problems and alternatives; discussing decision types like certainty, risk, and uncertainty; and using decision trees to analyze large, complex problems by breaking them into smaller parts. The document also provides two alternative examples applying decision analysis concepts to a case study about a business owner deciding whether to purchase industrial robots.Decision analysis



Decision analysisYoung Alista
╠²
The document describes decision analysis and provides examples of how decision trees and tables can be used to capture complex decision-making processes. It discusses five parts of a decision-making model: identify the problem, formulate options, model the problem, analyze the model, and implement and test the solution. Anchoring and framing errors in judgment are explained with examples. Finally, the use of decision trees and tables is demonstrated on examples involving business policies and rules.Decision analysis



Decision analysisHarry Potter
╠²
The document describes decision analysis and decision making. It discusses identifying the problem, formulating a model, analyzing the model, testing results, and implementing solutions. It also discusses anchoring and framing biases that can influence decisions. Anchoring occurs when a trivial factor serves as a starting point for estimates. Framing affects how alternatives are perceived in terms of wins and losses. The way a problem is framed can influence choices. Decision trees and tables are described as ways to represent complex decisions involving multiple conditions. Creating decision models allows for a more rigorous analysis of problems compared to using narratives alone.Decision analysis



Decision analysisLuis Goldster
╠²
The document describes decision analysis and decision making. It discusses identifying the problem, formulating a model, analyzing the model, testing results, and implementing solutions. It also discusses anchoring and framing biases that can influence decisions. Anchoring occurs when a trivial factor serves as a starting point for estimates. Framing affects how alternatives are perceived in terms of wins and losses. The way a problem is framed can influence choices made. Decision trees and tables are described as ways to represent complex decisions and business logic involving multiple conditions. Creating decision models allows for a more rigorous analysis of problems compared to using only narrative descriptions.Decision analysis



Decision analysisFraboni Ec
╠²
The document describes decision analysis and decision making. It discusses identifying the problem, formulating a model, analyzing the model, testing results, and implementing solutions. It also discusses sources of errors like anchoring and framing biases. Anchoring occurs when people rely too heavily on the first piece of information when making decisions. Framing refers to how the options are presented, which can influence choices. The document provides examples to illustrate these concepts and emphasizes the importance of focusing on the consequences of choices rather than how problems are framed.Decision analysis



Decision analysisTony Nguyen
╠²
The document describes decision analysis and provides examples of how decision trees and tables can be used to analyze complex decisions. It discusses five parts of a decision-making model: identify the problem, formulate options, model the problem, analyze the model, and implement and test the solution. Anchoring and framing errors in judgment are described. Examples are provided to illustrate anchoring biases and how framing a problem as a sure win versus sure loss can influence choices. The use of decision trees to represent sequential decisions and incorporate uncertainty is demonstrated. Creating decision tables to systematically capture complex business rules is also illustrated.Decision analysis



Decision analysisJames Wong
╠²
The document describes decision analysis and decision making. It discusses identifying the problem, formulating a model, analyzing the model, testing results, and implementing solutions. It also discusses anchoring and framing biases that can influence decisions. Anchoring occurs when people rely too heavily on an irrelevant starting value. Framing means how a decision is perceived, such as in terms of gains or losses, can influence choices. The document provides an example where how a coin flip problem is framed affects whether people prefer a sure outcome or chance of gain/loss. Effective decision making requires understanding values, objectives, uncertainties, and consequences of options.Lecture 4: NBERMetrics



Lecture 4: NBERMetricsNBER
╠²
This document summarizes a lecture on using moment inequalities to estimate preference parameters from discrete choice models. It discusses how this approach differs from standard empirical models by working directly with the inequalities that define optimal behavior. The approach assumes the utility from the actual choice should be larger than the utility from a considered but discarded counterfactual choice. Parameter values that satisfy these inequalities on average are accepted. The document then provides a single agent example to illustrate this approach.Making Decisions Presentation



Making Decisions Presentationandyped
╠²
This document discusses different approaches to decision making including certainty, uncertainty, and risk. It begins with an outline of the chapter which describes how managers need structure to make decisions in complex conditions. It then covers decision making with certainty, uncertainty using criteria like Laplace, Wald, and Savage, risk using expected values, and sequential decisions using decision trees. Limitations of the criteria are noted.Questions To Ask An Optimization Vendor



Questions To Ask An Optimization Vendorsourcingdoctor
╠²
Trying to find the right strategic sourcing decision optimization solution can be very confusing. Asking the right questions will go a long way towards finding the right solution.MBA 623_Decision Theory presentation for masters degree class.pptx



MBA 623_Decision Theory presentation for masters degree class.pptxjcsan1992
╠²
masteral subject for operations managementChristian decision making



Christian decision makingChristian Tobing
╠²
This document discusses different approaches to decision making under uncertainty, including maximin, expected monetary value, and multi-attribute utility analysis. It explains that maximin is inherently pessimistic by only considering the worst possible outcome for each option. Expected monetary value focuses only on monetary attributes and assumes a linear value function for money. Multi-attribute utility analysis derives single-attribute utility functions and combines them to evaluate options based on multiple attributes like time, cost, and risk preferences. It can incorporate non-monetary attributes if preferences conform to specific axioms.Jabina
- 1. Topic 11: Decision Making Sometimes we make decisions using information involving uncertainty, such as future weather conditions. In this topic, we will consider decisions based on information we already know, or can find. These types of decisions are called decisions under certainty. Give an example of a decision under certainty: Purchasing food at a food booth. Give an example of a decision not under certainty: Choosing between investment options which are based on stock values. Many times, decisions under certainty involve several criteria. One method we can use to help decide is the cutoff screening method. Here, the decision maker predetermines a cutoff for each criterion. Then, the decision maker goes through each criteria and eliminates any choices that don't meet the cutoff. If more than one choice remains, the decision maker could consider additional criteria or restrict the cutoffs. If all choices have been eliminated, the decision maker can relax the cutoffs. Another method to handle decisions under certainty with multiple criterion is the weighted sum method. In it, an "importance factor," or weight, is assigned to each criterion, and a rating is set up within each criterion. The ratings within each criteria should be consistent, and typically the highest rating used is 10. Similarly, a weight of 10 is assigned to the most important criterion, and the remaining weights will be assigned relative to the most important. Finally, a weighted sum will be calculated for each case. This will result in a single numerical rating, with the highest weighted sum giving the preferred choice. Term used in a situation when for each decision alternative there is only one event and therefore only one outcome for each action. For example, there is only one possible event for the two possible actions: "Do nothing" at a future cost of $3.00 per unit for 10,000 units, or "rearrange" a facility at a future cost of $2.80 for the same number of units. A decision matrix (or payoff table) would look as follows: Note that there is only one state of nature in the matrix because there is only one possible outcome for each action (with certainty). The decision is obviously to choose the action that will result in the most desirable outcome (least cost), that is to "rearrange." See also decision theory. Read more: http://www.answers.com/topic/decision-making-under-certainty#ixzz29qdkzNjX
- 2. What is an unbalanced problem Often, you will get a transportation problem where the total supply does not equal the total demand. For example, in the table below. Warehouse 1 Warehouse 2 Warehouse 3 Supply Bakery 1 5 8 4 7 Bakery 2 7 2 8 10 Demand 6 8 9 The total demand exceeds the total supply, so clearly, not all warehouses will get their total order. 'Dummy' Dealers and Suppliers In cases where you have unbalanced problems, this is solved by introducing a dummy supplier or dealer which can meet the excess. Clearly, they will not really be able to supply or take in loaves of bread, but we can make this adjustment at the end. Warehouse 1 Warehouse 2 Warehouse 3 Supply Bakery 1 5 8 4 7 Bakery 2 7 2 8 10 Dummy 0 0 0 6 Demand 6 8 9 It costs nothing to transport to and from the dummy, because it doesn't really exist. You can now use the algorithms and formulate linear programming problems as you did before.

