Jurnal statistika probabilitas distribusi binomial
12 likes17,217 views
Makalah ini membahas distribusi binomial, yaitu distribusi probabilitas diskret yang menghitung keberhasilan dalam n percobaan ya/tidak dengan peluang sama pada setiap percobaan. Distribusi binomial digunakan untuk menghitung peluang sukses dari beberapa percobaan yang independen dengan dua kemungkinan hasil. Makalah ini menjelaskan konsep, rumus, dan contoh soal distribusi binomial serta cara menghitungnya menggunakan Microsoft Excel.
![Makalah Statistika Probabilitas |STMIK Provisi 2013 3
Gambar 4. Function Arguments
Nilai yang akan keluar adalah 0,8.
Terapkan cara tersebut untuk n, x dan p pada contoh soal.
Diketahui :
n = 5
x = 3
p = 0,7
Isilah variabel-variabel dalam fungsi tersebut;
Number_s (x) : B6 (sel yang memuat nilai x
= 3)
Trials (n) : A3 (sel yang memuat nilai n = 5)
Probability_s (p) : I2 = 0,7
Cumulative : 1
Klik OK
Gambar 5. Hasil Perhitungan
Nilai yang akan keluar adalah 0,47178 atau
dibulatkan ke atas menjadi 0,4718
Rata-rata dan Varian Distribusi Binomial b(x; n, p)
adalah
Rata-rata = np
Varian 族 = npq
n = ukuran populasi
p = peluang keberhasilan setiap ulangan
q = 1 - p = peluang gagal setiap ulangan
3. Dari soal nomor 1, hitunglah rata-rata dan
variannya!
Jawab :
= np
= 5 x 0,7
= 3,5
族 = npq
= 5 x 0,7 x 0,3
= 1,05
IV. Kesimpulan
Dari uraian tersebut kami menyimpulkan bahwa
probabilitas sangatlah membantu dalam mengambil
suatu keputusan. Misalnya menentukan peluang sukses
atau tidak dalam dunia bisnis dan usaha.
Distribusi Binomial ditemukan oleh James
Bernoulli yang kemudian dikembangkan menjadi
Distribusi Binomial, yaitu merupakan suatu percobaan
dimana hanya ada 2 outcome (hasil), seperti sukses dan
gagal.
Rumus yang dipakai adalah .
n-xxn
x qpCx)P(Xb(x;n,p) 緒緒
Untuk menentukan rata-rata adalah = np, dan untuk
menentukan varian atau ragam adalah 蛎 = npq.
REFERENSI
Sudaryono, M.Pd. 2011. STATISTIKA PROBABILITAS
[Teori & Aplikasi]. Tangerang: Penerbit ANDI
http://id.wikipedia.org/wiki/Distribusi_binomial
diakses hari Sabtu tanggal 15 bulan Juni tahun
2013 pukul 10.38 WIB.
http://id.scribd.com/doc/122282828/MAKALAH-
ProbStat-Distribusi-Binomial
diakses hari Sabtu tanggal 15 bulan Juni tahun
2013 pukul 10.07 WIB.
http://www.slideshare.net/cvrhmat/distribusi-peluang
diakses hari Sabtu tanggal 15 bulan Juni tahun
2013 pukul 11.52 WIB.
http://images.tutorvista.com/cms/images/67/cumulative
-binomial-distribution.jpg
diakses/didownload hari Sabtu tanggal 15 bulan
Juni tahun 2013 pukul 11.56 WIB.
Biodata Penulis
Yehezkiel Yanu Putranto, lahir di kota
Semarang pada tanggal 1 Januari 1993.
Alumnus dari TK Tunas Harapan, SD
Negeri Tirtoyoso 01-02, SMP Negeri 6
Semarang, SMK Negeri 5 Semarang. Kini
sedang menyelesaikan studi Strata 1 di
STMIK Provisi Semarang yang berkonsentrasi pada
jurusan Teknik Informatika.](https://image.slidesharecdn.com/jurnalstatistikaprobabilitas-distribusibinomial-130628043747-phpapp02/85/Jurnal-statistika-probabilitas-distribusi-binomial-3-320.jpg)
Jurnal statistika probabilitas distribusi binomial
- 1. Makalah Statistika Probabilitas |STMIK Provisi 2013 1 DISTRIBUSI BINOMIAL Yehezkiel Yanu Putranto (114111326) Program Studi Teknik Informatika, STMIK Provisi Semarang Email: jc.masterboyz4ever@gmail.com Abstrak Distribusi Binomial adalah salah satu dari beberapa distribusi probabiltias untuk menghitung peluang suatu kejadian. Distribusi Binomial menggunakan variable diskret dimana hasilnya (outcome) hanya memiliki dua kemungkinan, seperti sukses atau gagal, tinggi atau rendah, dsb. Kata kunci: Distribusi; Binomial; Peluang; Diskret I. PENDAHULUAN Dalam teori probabilitas dan statistika, distribusi binomial adalah distribusi probabilitas diskret jumlah keberhasilan dalam n percobaan ya/tidak (berhasil/gagal) yang saling bebas, dimana setiap hasil percobaan memiliki probabilitas p. Eksperimen berhasil/gagal juga disebut percobaan bernoulli. Ketika n = 1, distribusi binomial adalah distribusi bernoulli. Distribusi binomial merupakan dasar dari uji binomial dalam uji signifikansi statistik. Distribusi ini seringkali digunakan untuk memodelkan jumlah keberhasilan pada jumlah sampel n dari jumlah populasi N. Apabila sampel tidak saling bebas (yakni pengambilan sampel tanpa pengembalian), distribusi yang dihasilkan adalah distribusi hipergeometrik, bukan binomial. Semakin besar N daripada n, distribusi binomial merupakan pendekatan yang baik dan banyak digunakan. II. Landasan Teori Disebut pula distribusi BERNOULLI ditemukan oleh JAMES BERNOULLI adalah suatu distribusi teoritis yang menggunakan variable acak diskrit (variable yang hanya memiliki nilai tertentu, nilainya merupakan bilangan bulat dan asli tidak berbentuk pecahan) yang terdiri dari dua kejadian yang berkomplementer seperti sukses-gagal, baik- cacat, siang malam, dsb. Syarat-syarat Distribusi Binomial : 1. Jumlah percobaan merupakan bilangan bulat, contohnya seuatu percobaan melambungkan koin sebanyak 3 kali, bukan 3 setengah kali. 2. Sebuah percobaan mempunyai dua outcome atau hasil, contohnya sukses atau gagal, sakit atau sehat, hidup atau mati, dsb. 3. Peluang sukses sama pada setiap percobaannya. Ciri-ciri Distribusi Binomial : Setiap percobaan hanya memiliki dua peristiwa, seperti sukses-gagal Probabilitas satu peristiwa adalah tetap, tidak berubah untuk setiap perubahan Percobaannya bersifat independen, artinya peristiwa dari suatu percobaan tidak mempengaruhi atau dipengaruhi peristiwa dalam percobaan lainnya Jumlah atau banyaknya percobaan yang merupakan komponen percobaan binomial harus tetap Beberapa contoh kasus penerapan Distribusi Binomial ini adalah : 1. Menghitung jumlah probabilitas dalam pelemparan dadu ataupun koin. 2. Menghitung jumlah lemparan bebas yang dilakukan oleh pemain basket. 3. Menghitung jumlah pertanyaan yang dapat anda jawab dengan benar pada sebuah soal pilihan ganda. Definisi Distribusi Peluang Binomial untuk x = 0,1,23,...,n n: banyaknya ulangan x: banyak keberhasilan dalam peubah acak X p: peluang berhasil pada setiap ulangan q: peluang gagal = 1 - p pada setiap ulangan III. Pembahasan Contoh soal : 1. Probabilitas bahwa sejenis mobil tertentu yang lolos uji emisi adalah 0,7. Tentukan dimana 3 dari 5 mobil yang selanjutnya diujikan dinyatakan lolos! 2. Pada soal no 1, tentukan nilai P(X<3) dengan mengacu pada table distribusi komulatif Binomial! Jawab : 1. n-xxn x qpCx)P(X 緒 x = 3; n = 5; p = 0,7 q = 1-0,7 = 0,3 3535 3 3,07,03 - C)P(X 緒 = 5! 3! 2! . 0,343 . 0,09 = 10. 0,343 . 0,09 = 0,3087 n-xxn x qpCx)P(Xb(x;n,p) 緒緒
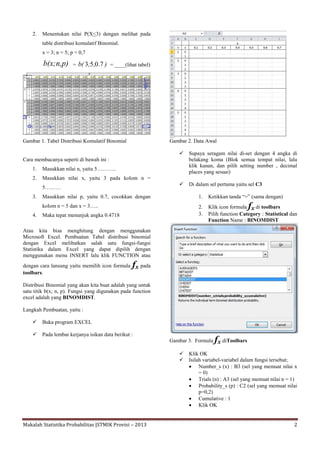
- 2. Makalah Statistika Probabilitas |STMIK Provisi 2013 2 2. Menentukan nilai P(X<3) dengan melihat pada table distribusi komulatif Binomial. x = 3; n = 5; p = 0,7 b(x;n,p) = ),;b( 7.053 = ____(lihat tabel) Gambar 1. Tabel Distribusi Komulatif Binomial Cara membacanya seperti di bawah ini : 1. Masukkan nilai n, yaitu 5.. 2. Masukkan nilai x, yaitu 3 pada kolom n = 5 3. Masukkan nilai p, yaitu 0.7, cocokkan dengan kolom n = 5 dan x = 3.. 4. Maka tepat menunjuk angka 0.4718 Atau kita bisa menghitung dengan menggunakan Microsoft Excel. Pembuatan Tabel distribusi binomial dengan Excel melibatkan salah satu fungsi-fungsi Statistika dalam Excel yang dapat dipilih dengan menggunakan menu INSERT lalu klik FUNCTION atau dengan cara lansung yaitu memilih icon formula fx pada toolbars. Distribusi Binomial yang akan kita buat adalah yang untuk satu titik b(x; n, p). Fungsi yang digunakan pada function excel adalah yang BINOMDIST. Langkah Pembuatan, yaitu : Buka program EXCEL Pada lembar kerjanya isikan data berikut : Gambar 2. Data Awal Supaya seragam nilai di-set dengan 4 angka di belakang koma (Blok semua tempat nilai, lalu klik kanan, dan pilih setting number , decimal places yang sesuai) Di dalam sel pertama yaitu sel C3 1. Ketikkan tanda = (sama dengan) 2. Klik icon formula fx di toolbars 3. Pilih function Category : Statistical dan Function Name : BINOMDIST Gambar 3. Formula fx diToolbars Klik OK Isilah variabel-variabel dalam fungsi tersebut; Number_s (x) : B3 (sel yang memuat nilai x = 0) Trials (n) : A3 (sel yang memuat nilai n = 1) Probability_s (p) : C2 (sel yang memuat nilai p=0,2) Cumulative : 1 Klik OK
- 3. Makalah Statistika Probabilitas |STMIK Provisi 2013 3 Gambar 4. Function Arguments Nilai yang akan keluar adalah 0,8. Terapkan cara tersebut untuk n, x dan p pada contoh soal. Diketahui : n = 5 x = 3 p = 0,7 Isilah variabel-variabel dalam fungsi tersebut; Number_s (x) : B6 (sel yang memuat nilai x = 3) Trials (n) : A3 (sel yang memuat nilai n = 5) Probability_s (p) : I2 = 0,7 Cumulative : 1 Klik OK Gambar 5. Hasil Perhitungan Nilai yang akan keluar adalah 0,47178 atau dibulatkan ke atas menjadi 0,4718 Rata-rata dan Varian Distribusi Binomial b(x; n, p) adalah Rata-rata = np Varian 族 = npq n = ukuran populasi p = peluang keberhasilan setiap ulangan q = 1 - p = peluang gagal setiap ulangan 3. Dari soal nomor 1, hitunglah rata-rata dan variannya! Jawab : = np = 5 x 0,7 = 3,5 族 = npq = 5 x 0,7 x 0,3 = 1,05 IV. Kesimpulan Dari uraian tersebut kami menyimpulkan bahwa probabilitas sangatlah membantu dalam mengambil suatu keputusan. Misalnya menentukan peluang sukses atau tidak dalam dunia bisnis dan usaha. Distribusi Binomial ditemukan oleh James Bernoulli yang kemudian dikembangkan menjadi Distribusi Binomial, yaitu merupakan suatu percobaan dimana hanya ada 2 outcome (hasil), seperti sukses dan gagal. Rumus yang dipakai adalah . n-xxn x qpCx)P(Xb(x;n,p) 緒緒 Untuk menentukan rata-rata adalah = np, dan untuk menentukan varian atau ragam adalah 蛎 = npq. REFERENSI Sudaryono, M.Pd. 2011. STATISTIKA PROBABILITAS [Teori & Aplikasi]. Tangerang: Penerbit ANDI http://id.wikipedia.org/wiki/Distribusi_binomial diakses hari Sabtu tanggal 15 bulan Juni tahun 2013 pukul 10.38 WIB. http://id.scribd.com/doc/122282828/MAKALAH- ProbStat-Distribusi-Binomial diakses hari Sabtu tanggal 15 bulan Juni tahun 2013 pukul 10.07 WIB. http://www.slideshare.net/cvrhmat/distribusi-peluang diakses hari Sabtu tanggal 15 bulan Juni tahun 2013 pukul 11.52 WIB. http://images.tutorvista.com/cms/images/67/cumulative -binomial-distribution.jpg diakses/didownload hari Sabtu tanggal 15 bulan Juni tahun 2013 pukul 11.56 WIB. Biodata Penulis Yehezkiel Yanu Putranto, lahir di kota Semarang pada tanggal 1 Januari 1993. Alumnus dari TK Tunas Harapan, SD Negeri Tirtoyoso 01-02, SMP Negeri 6 Semarang, SMK Negeri 5 Semarang. Kini sedang menyelesaikan studi Strata 1 di STMIK Provisi Semarang yang berkonsentrasi pada jurusan Teknik Informatika.