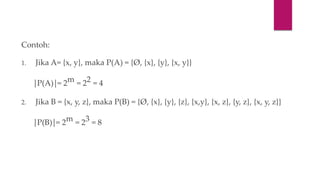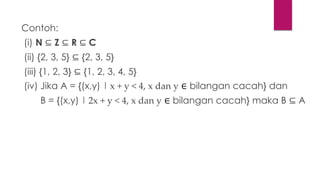�ݺ�ߣ

KARDINALITAS
Oleh : Emanueli Mendrofa, S.Pd
Mata Kuliah : Teori Himpunan dan Logika Matematika

Definisi Kardinalitas
 Jumlah atau banyaknya elemen suatu himpunan berhingga dinamakan
kardinalitas.
 Untuk menyatakan kardinalitas himpunan A ditulis dengan notasi: n(A) atau ⏐A⏐
 Contoh:
(i) B = { x | x merupakan bilangan prima yang lebih kecil dari 20 },
atau B = {2, 3, 5, 7, 11, 13, 17, 19} maka ⏐B⏐ = 8
(ii) K = {kucing, a, Aril, 31, penggaris}, maka ⏐K⏐= 5
(iii) Jika N = {x | x² - 8x + 12 = 0} maka ⏐N⏐= 2

Himpunan Kuasa
Himpunan kuasa (power set) dari himpunan A merupakan suatu himpunan yang unsur-unsurnya
merupakan semua himpunan bagian dari A, termasuk himpunan kosong dan himpunan A
sendiri.
Himpunan kuasa dinotasikan oleh P(A). Jumlah anggota (kardinal) dari suatu himpunan kuasa
bergantung pada kardinal himpunan asal. Misalkan, kardinalitas himpunan A adalah m, maka
⏐P(A)⏐= 2m.

Contoh:
1. Jika A= {x, y}, maka P(A) = {Ø, {x}, {y}, {x, y}}
⏐P(A)⏐= 2m = 22 = 4
2. Jika B = {x, y, z}, maka P(B) = {Ø, {x}, {y}, {z}, {x,y}, {x, z}, {y, z}, {x, y, z}}
⏐P(B)⏐= 2m = 23 = 8

PENGERTIAN
Relasi antara dua buah himpunan adalah
pernyataan yang mendefinisikan hubungan
antara suatu himpunan dengan himpunan
lainnya.

Himpunan Bagian
 Himpunan A dikatakan himpunan bagian (subset) dari himpunan B jika dan hanya jika
setiap unsur A merupakan unsur dari B. Dalam hal ini, B dikatakan superset dari A.
 Notasi himpunan bagian : A ⊆ B atau A ⊂ B
 Diagram Venn himpunan bagian:
A
B
S

Contoh:
(i) N ⊆ Z ⊆ R ⊆ C
(ii) {2, 3, 5} ⊆ {2, 3, 5}
(iii) {1, 2, 3} ⊆ {1, 2, 3, 4, 5}
(iv) Jika A = {(x,y) | x + y < 4, x dan y ∈ bilangan cacah} dan
B = {(x,y) | 2x + y < 4, x dan y ∈ bilangan cacah} maka B ⊆ A
Anggota himpunan dari:
A = {(0,0); (0,1); (0,2); (0,3); (1,0); (2,0); (3,0); (1,1); (1,2); (2,1)}
B = {(0,0); (0,1); (0,2); (0,3); (1,(1,1)}

Untuk sembarang himpunan A berlaku hal-hal sebagai
berikut:
(a) A adalah himpunan bagian dari A itu sendiri (yaitu, A ⊆
A).
(b) Himpunan kosong merupakan himpunan bagian dari A
(Ø ⊆ A).
(c) Jika A ⊆ B dan B ⊆ C, maka A ⊆ C

Ø ⊆ A dan A ⊆ A, maka Ø dan A disebut himpunan bagian
tak sebenarnya/sejati (improper subset) dari himpunan A.
Contoh: A = {1, 2, 3}, maka {1, 2, 3} dan Ø adalah improper
subset dari A.

 A  B berbeda dengan A  B
(i) jika A  B maka A adalah himpunan bagian dari B tetapi
A  B.
A adalah himpunan bagian sebenarnya/sejati (proper
subset) dari B.
Contoh: {1} dan {2, 3} adalah proper subset dari {1, 2, 3}
(ii) A  B digunakan untuk menyatakan bahwa A adalah
himpunan bagian (subset) dari B yang memungkinkan A
= B.

Latihan
Misalkan A = {1, 2, 3} dan B = {1, 2, 3, 4, 5}. Tentukan semua
kemungkinan himpunan C sedemikian sehingga A  C dan
C  B, dan C adalah proper subset dari B.

Jawaban:
C harus mengandung semua elemen A = {1, 2, 3} dan
sekurang-kurangnya satu elemen dari B.
Dengan demikian, C = {1, 2, 3, 4} atau
C = {1, 2, 3, 5}.
C tidak boleh memuat 4 dan 5 sekaligus karena C adalah
proper subset dari B.

HIMPUNAN SALING LEPAS
Dua himpunan A dan B dikatakan saling lepas (disjoint) jika
keduanya tidak memiliki elemen yang sama.
Notasi yang digunakan adalah A // B.
Jika dinyatakan dalam bentuk diagram Venn adalah sebagai
berikut:
A B
S

Contoh:
1. L = {1, 3, 5, 7, 9, 11, 13, 15}
G = {2, 4, 6, 8, 10, 12, 14, 16}
Coba kalian perhatikan, adakah anggota himpunan L dan G yang
sama?
Karena tidak ada anggota himpunan L dan G yang sama maka
himpunan L dan G adalah dua himpunan yang saling lepas, jadi L //
G
2. Jika A = { x| x ∈ N, x < 10 } dan B = { 11, 12, 13, 14, 15 },
maka A // B

HIMPUNAN BERPOTONGAN
Himpunan A dan B dikatakan berpotongan (tidak saling lepas) jika
dan hanya jika ada elemen A yang menjadi elemen B.
Contoh:
1. P = {1, 2, 3, 4, 5, 6, 7, 8}
Q = {2, 4, 6, 8, 10, 12, 14, 16}
Elemen himpunan P yang menjadi elemen himpunan Q adalah
2, 4, 6, dan 8. jadi himpunan P berpotongan dengan himpunan
Q.

2. A = {x | x² - 8x + 12 = 0} dan B = {x | x² - 4 = 0}
A dan B berpotongan
3. A = {x | x² - 8x + 12 = 0} dan B = {1, 3, 5}
A dan B tidak berpotongan

HIMPUNAN SAMA
Dua buah himpunan dikatakan sama jika memenuhi kondisi berikut:
Jika dan hanya jika setiap unsur A merupakan unsur B dan
sebaliknya setiap unsur B merupakan unsur A.
Untuk menyatakan A = B, yang perlu dibuktikan adalah A adalah
himpunan bagian dari B dan B merupakan himpunan bagian dari
A. Jika tidak demikian, maka A ≠ B.
atau
A = B ⟺ A ⊆ B dan B ⊆ A

CONTOH
1. K = {x | x² - 3x + 2 = 0}
L = {1, 2}
Maka K = L
2. Jika A = { 0, 1 } dan B = { x| x (x – 1) = 0 },
maka A = B
3. Jika A = { 3, 5, 8, 5 } dan B = {5, 3, 8 },
maka A = B

4. Jika A = { 3, 5, 8, 5 } dan B = {3, 8},
maka A ≠ B
Untuk tiga buah himpunan, A, B, dan C berlaku aksioma berikut:
(a) A = A, B = B, dan C = C
(b) Jika A = B, maka B = A
(c) Jika A = B dan B = C, maka A = C
Aksioma adalah pernyataan yang dapat diterima sebagai kebenaran tanpa
pembuktian

Himpunan Ekivalen
Dua buah himpunan dikatakan ekivalen jika masing-masing mempunyai kardinalitas
yang sama. Misalkan, himpunan A adalah ekivalen dengan himpunan B berarti
kardinal dari himpunan A dan himpunan B adalah sama, notasi yang digunakan
adalah : A ~ B.
Contoh:
Misalkan A = { 2, 3, 5, 7 } dan B = { a, b, c, d},
maka A ~ B sebab ⏐A⏐ = ⏐B⏐ = 4

TUGAS
1. Jika diketahui A = {1, 2, 3, 4}, berapa banyak
himpunan bagian dari A? Sebutkan!
2. Jika P = {jajargenjang}, Q = {belah ketupat}, R =
{persegi}, dan T = {persegi panjang} pada bidang
datar.
Tentukan relasi antar himpunan-himpunan
tersebut!
Tentukan diagram venn untuk melukiskan relasi
antar himpunan P, Q, R, dan T

TUGAS
3. Diketahui P  Q dan Q  R. Misalkan p ∈ P, q ∈ Q, r
∈ R dan juga t ∉ P, u ∉ Q, v ∉ R. Mana diantara
pernyataan berikut yang benar?
 p ∈ R
 q ∉ P
 v ∈ R
 t ∉ R
 P  R

Kardinalitas dan Operasi Dua Himpunan

�ݺ�ߣ

Kardinalitas dan Operasi Dua Himpunan

More Related Content

Kardinalitas dan Operasi Dua Himpunan