�ݺ�ߣ

KELOMPOK 1
FAUZIAH
ISTI ASHARI RACHMAN
A. RESKIANTI ARDI
UMMUL J.
KAMARUDDIN

UJI HIPOTESIS TENTANG
RERATA
RERATA SEBUAH POPULASI

Uji Hipotesis tentang Rerata
• Rerata adalah salah satu ukuran gejala pusat
yang banyak digunakan dalam mengungkap
informasi dari sekumpulan data
• Yang akan kita bahas adalah
RERATA SEBUAH POPULASI

Rerata
Sebuah
Populasi
Simpangan
baku 𝜎
diketahui
Simpangan
baku 𝜎 tidak
diketahui

Simpangan baku 𝝈 diketahui
• Statistik z dengan rumus:
𝑧 =
𝑥 − 𝜇0
𝜎 𝑛
• Hipotesis Uji dua pihak
1. H0 diterima jika −𝑧(1−𝛼)/2≤ 𝑧 ≤ 𝑧(1−𝛼)/2
2. H0 ditolak jika 𝑧 < −𝑧(1−𝛼)/2 atau 𝑧 > 𝑧(1−𝛼)/2.
• Hipotesis Uji pihak kanan
1. H0 diterima jika 𝑧 ≤ 𝑧 0,5−𝛼
2. H0 ditolak jika 𝑧 > 𝑧(0,5−𝛼)
• Hipotesis Uji pihak kiri
1. H0 diterima jika 𝑧 ≥ −𝑧 0,5−𝛼
2. H0 ditolak jika 𝑧 < −𝑧(0,5−𝛼)

Simpangan baku 𝝈 tidak diketahui
• Rumus statistic yang digunakan:
𝑡 =
𝑥 − 𝜇0
𝑠 𝑛
• Hipotesis Uji dua pihak
1. H0 diterima jika – 𝑡1−𝛼
2
≤ 𝑡 ≤ 𝑧1−𝛼
2
2. H0 ditolak jika 𝑡 < −𝑡(1−𝛼)/2 atau 𝑡 > 𝑡(1−𝛼)/2
• Hipotesis Uji pihak kanan
1. H0 diterima jika 𝑡 ≤ 𝑡 1−𝛼
2. H0 ditolak jika 𝑡 > 𝑡(1−𝛼)
• Hipotesis Uji pihak kiri
1. 𝐻0 diterima jika 𝑡 ≥ −𝑡 1−𝛼
2. 𝐻0 diitolak jika 𝑡 < −𝑡(1−𝛼)

Contoh 1
Pabrik lamou pijar A mengatakan bahwa
lampunya bisa tahan sekitas 1000 jam. Akhir-
akhir ini timbul dugaan bahwa masa pakai lapu itu
sudah menurun. Untuk mengji dugaan ini,
penelitian dilakukan terhadap 75 bola lampu.
Hasil yang diperoleh ialah rerata masa pakai 𝑥 =
980. Dari pengalam diketahui bahwa simpangan
baku masa hidup lampu itu 45 jam. Selidikilah
dengan taraf signifikan 5% apakah mutu lampu
tersebut benar menurun?

Jawaban
• Penelitian akan menguji hipotesis: Mutu lampu pijar
A sudah menurun
• Hipotesis yang akan diuji 𝐻0: 𝜇 = 1000 melawan
𝐻1: 𝜇 < 1000 atau yang ekuivalen 𝐻0: 𝜇 ≥ 1000
melawan 𝐻1: 𝜇 < 1000
• Karena simpangan baku populasi diketahui, yaitu
𝜎 = 45 jam, statistik yang sesuai adalah =
𝑥−𝜇0
𝜎 𝑛
.
karena rerata 𝑥 = 980, 𝑛 = 75, maka 𝑧 = −3,85
• Nilai kritis untuk −𝑧0,45= −1,645 menunjukkan
bahwa nilai statistik 𝑧 = −3,85 < −𝑧0,45= −1,645,
sehingga kesimpulannya adalah 𝐻0 ditolak

Contoh 2
Seorang peneliti ingin menguji hipotesisi tentang
rerata berat bayi yang baru lahir di suatu rumah
barsalin. Sampel sepuluh orang bayi yang baru
lahir memberikan data berat (dalam Kg): 2,5 2,6
2,8 2,8 3,1 2,9 3,0 3,9 2,6 2,6. Ujilah 𝐻0: 𝜇 = 3 kg
melawan 𝐻1: 𝜇 < 3 kg pada taraf signifikasi 𝛼 =
5%

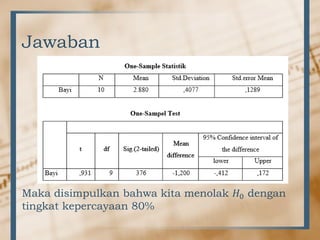
Jawaban
Maka disimpulkan bahwa kita menolak 𝐻0 dengan
tingkat kepercayaan 80%

�ݺ�ߣ

KELOMPOK 1.pptx

More Related Content

Similar to KELOMPOK 1.pptx (15)

Recently uploaded (20)

KELOMPOK 1.pptx