Keseimbangan benda tegar
- 1. Keseimbangan benda tegar SMA Indnesia
- 2. Mekanika memiliki tiga cabang: 1.Kinematika 2.Dinamika 3.Statika
- 3. Kinematika Ilmu yang mempelajari gerak tanpa mempedulikan penyebabnya
- 4. Dinamika Ilmu yang mempelajari gerak dengan melibatkan gaya sebagai penyebab perubahan gerak
- 5. Statika Adalah cabang mekanika yang mempelajari gaya-gaya yang bekerja pada suatu benda yang ada dalam keseimbangan dan diam
- 7. Partikel Adalah benda yang ukurannya dapat diabaikan
- 8. Syarat partikel seimbang Resultan gaya yang bekerja pada partikel adalah nol (Hukum pertama Newton) ΣF = 0
- 9. Untuk satu dimensi Σ Fx = 0 Untuk dua dimensi Σ Fx = 0 Σ Fy = 0 Untuk tiga dimensi Σ Fx = 0 Σ Fy = 0 Σ Fz = 0
- 10. Contoh untuk satu dimensi T ΣF = 0 25 N 25 N T-w = 0 T = w T = 25 N w
- 11. Contoh untuk dua dimensi 370 530 400 N
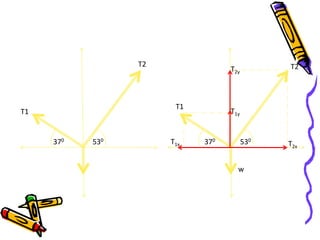
- 12. T2 T2 T2y T1 T1 T1y 370 530 T1x 370 530 T2x w
- 13. Untuk sumbu x Σ Fx = 0 T2x – T1x = 0 T2 cos 530 – T1 cos 370 = 0 0.6 T2 – 0.8T1 = 0 0.75T2 = T1 Dengan memasukan T2 0.75T2 = T1 Untuk sumbu y 0.75(320) = T1 Σ Fy = 0 240 = T1 T1y + T2y - w = 0 T1 sin 370 + T2 sin 530 = w 0.6 T1 + 0.8T2 = 400 0.6(0.75T2) + 0.8T2 = 400 400/1.25 = T2 320 = T2
- 14. Dengan Persamaan sinus F2 F1 ά3 ά1 ά2 F1 F2 F3 = = F3 sin ά1 sin ά2 sin ά3
- 16. Benda Tegar Adalah benda yang tidak berubah bentuknya bila diberi gaya luar
- 17. Syarat benda tegar seimbang ΣF = 0 Σ = 0
- 18. Contoh: 300 A B 8N Pada ujung batang AB digantungkan sebuah beban 8 N. Bila massa batang AB diabaikan hitung tegangan tali?
- 19. T sin 300 T 300 A B T cos 300 L 8N Σ A = 0 L 8 – L T sin 300 = 0 8 L = L T sin 300 8 = 0.5 T T = 16 N
- 20. Contoh : Batang BC bersandar pada dinding licin dan bertumpu pada lantai kasar. Hitung koefisien gesekan di B pada saat batang tepat akan bergeser? C 4m 5m A A B
- 21. Fx = 0 C Nc Nc - f = 0 Nc = f 4m 5m Σ A = 0 4 NC + 1.5 w – 3 NB = 0 w NB 4 NC + 1.5 w – 3 w = 0 4 NC = 1.5 w NC = 0.375 f A B w NC = f 0.375 w = w 0.375 =
- 22. Contoh: 10 N O 40 N A B X=… Batang AB panjangnya 1 m. Agar batang AB horisontal , hitunglah jarak x.?
- 23. Σ O = 0 40 (1 –x) - 10 x = 0 40 – 40 x – 10 x = 0 40 = 50 x x = 0.8 m
- 24. Latihan 1 Dua orang bersaudara hendak memikul sebuah beban dengan menggunakan tongkat pemikul. Keduanya memikul pada ujung-ujung tongkat yang berlawanan. Kakak harus memikul 50% lebih berat benda dari adiknya. Jika panjang tongkat pemikul panjang 2 meter, dimanakah benda tersebut digantungkan? Latihan 2 Batang homogen beratnya 50 N, seperti tampak pada Gambar, berada 37 dalam keadaan seimbang. Hitunglah tegangan kabel pendukung dan 100 cm 40 cm komponen-komponen gaya yang dikerjakan oleh engsel pada batang. 100 N
- 25. TITIK BERAT
- 26. MENENTUKAN TITIK BERAT DENGAN PERCOBAAN Buat tiga lubang Titik berat …….? C A B
- 30. Dengan perhitungan y (x3,y3 (x1,y1 ) ) (x0,y0 ) (x2,y2 w3 w1 ) w2 w x 0 x1w1 + x2w2 + x3w3 + … x0 = w1 + w2 + w3 + … y1w1 + y2w2 + y3w3 + … y0 = w1 + w2 + w3 + …
- 31. Menghitung titik berat dari massa partikel x1m1g+x2m2g+x3m3g+ … w = mg x0 = m1g+m2g+m3g + … x1m1+x2m2+x3m3+ … x0 = m1+m2+m3 + … y1m1 + y2m2 + y3m3 + … y0 = m1 + m2 + m3 + …
- 32. Menghitung titik berat benda homogen berdimensi tiga x1V1 +x2V2 +x3V3 + … m= V x0 = V1 +V2 +V3 + … x1V1+x2V2+x3V3+ … x0 = V1+V2+V3+ … y1V1 + y2V2 + y3V3 + … y0 = V1 + V2 + V3 + …
- 33. Menghitung titik berat benda homogen berdimensi dua x1A1t+x2A2t+x3A3t+ … V = At x0 = A1t+A2t+A3t+ … x1A1+x2A2+x3A3+ … x0 = A1+A2+A3+ … y1A1 + y2A2 + y3A3 + … y0 = A1 + A2 + A3 + …
- 34. Menghitung titik berat benda homogen berdimensi dua x1pl1+x2pl2+x3pl3+ … A=pl x0 = pl1+pl2+pl3+ … x1l1+x2l2+x3l3+ … x0 = l1+l2+l3+ … y1l1 + y2l2 + y3l3 + … y0 = l1 + l2 + l 3 + …
- 35. Macam-macam keseimbangan 1. Labil 2. Stabil 3. Netral