KMC 競技プログラミング練習会 Advanced 第3回 ふろー
?
3 likes?2,374 views
KMCの競技プログラミング練習会Advanced第3回を担当いたしました。 去年Normalでフローを行わなかったので, 基本からやっていきます.
KMC 競技プログラミング練習会 Advanced 第3回 ふろー
- 2. ? 最大流 ? 最小費用流 ? 応用 ? 線形計画問題 2 ふろー
- 3. ? 重み付き有向グラフ上で s から t まで どのくらい流せるか – 各辺の重みはその辺に流せる最大流量(容量) – 最大流問題 – 下の場合最大流は 9 s t 5 4 1 3 9 5 7 3 6 最大流
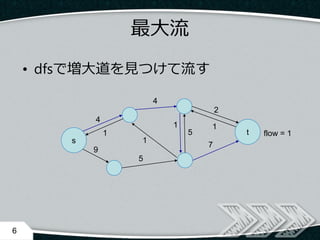
- 4. ? Ford-Fulkerson法 – ? ? ? – 残余グラフ(後述)上で 増大道(sからtに1以上流せるパス)を見つけて 流し続ける 4 s t 5 4 1 3 9 5 7 6 増大道 ─ に1を流す flow = 0 最大流
- 5. ? 残余グラフ ? = ?, ? ∈ ? に ? 流したら 逆辺 ?′ = ?, ? の容量を ? 増やす 5 s t 4 4 0 2 9 5 7 51 1 1 1 最大流 flow = 1
- 6. ? dfsで増大道を見つけて流す 6 s t 4 4 2 9 5 7 5 flow = 11 1 1 1 最大流
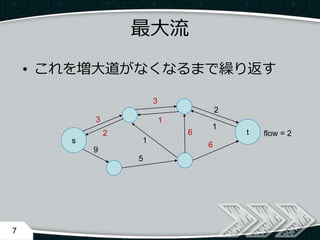
- 7. ? これを増大道がなくなるまで繰り返す 7 s t 3 3 2 9 5 6 6 flow = 22 1 1 1 最大流
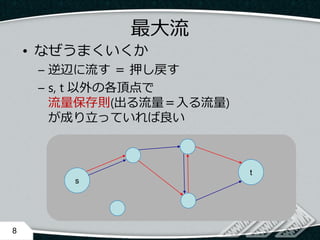
- 8. ? なぜうまくいくか – 逆辺に流す ＝ 押し戻す – s, t 以外の各頂点で 流量保存則(出る流量＝入る流量) が成り立っていれば良い 8 s t 最大流
- 9. 最大流 増大道がなくなったらそれが最大流 ∵ sから残余グラフ上で到達可能な頂点集合 Sを考えると, S→V＼T へ残余グラフ上で 辺がないから元のグラフではめいいっぱい 流れているのでこれ以上流せない 9
- 10. 最大流 増大道は dfs すれば ? ? で見つけられ, 1回流すと今まで合計で流した流量は 少なくとも1増えるので, 答えとなる流量を ? とすると ? ? ? . 10
- 11. 最大流 ? Ford-Fulkerson法は無駄が多そう – 遠回りして見つけたパスを後から近いルート で更新したりする – 計算量が ? に依存する ?s-t 間の距離が近い順に見ていく！ ?Dinicのアルゴリズム 11
- 12. 最大流 ? Dinicのアルゴリズム – dfsする前にbfsして, sから遠ざかっていく辺 だけを辿っていく – ? ? 2 ? (よりもかなり高速) 12 flow = 0; while (1) { update = false; bfsして各頂点のsからの距離を計算する; while ((f = dfsして増大道を見つけて流した流量) > 0) { flow += flow; update = true; } if (!update) return flow; }
- 13. 最大流 ? 容量スケーリング – 2 ? 単位で流せるだけ流すといった操作を ? を減らしていきながら繰り返す 13
- 14. 最小費用流 ? 各辺に容量だけでなくコストの重みもある ? その辺に流量1のフローを流したときに そのコストが発生する ? s – t 間に 流量 ? のフローを流したときの 合計コストを最小化したい 14
- 15. 最小費用流 ? アルゴリズム – コスト ? の辺の逆辺のコストを ?? とする – Ford-Fulkerson法の増大道を見つけるフェイズで dfsする代わりに Bellman–Ford を行い, s – t 最短経路を見つける – それだけ！！ – ?(? ? ? ) 15
- 16. 最小費用流 ? Bellman-Ford の部分を dijkstraにしたい ? 逆辺のせいで負の辺が現れるので dijkstra使えなさそう – 実は使える 16
- 17. 最小費用流 ? 各頂点にポテンシャルを良い感じに 設定するとdijkstraできる ? ポテンシャルとはゲタ的なもので, 各頂点のポテンシャルを ? ? とし, 辺? = ?, ? のコスト? ??を ? ?? ′ = ? ?? + ? ? ? ? ?として考えたときに 残余グラフ上の全ての辺で ? ?? ′ ≥ 0 であればdijkstraが使える！ 17
- 18. 最小費用流 1. 各頂点のポテンシャルを ? ? とする 2. 初期状態では ? ? = 0 とする 3. 初期状態で負コストの辺がなければ, dijkstraを1回まわせるので回してフローを流す 4. 回した結果, sからの距離を???? ?とする 5. 全ての? ?に???? ?を加える 6. すると, なぜか残余グラフ上でコストが正になるので 3にもどって反復的にできる (詳しくは蟻本) 18
- 19. 最小費用流 ? dijkstraを使えば? ? ? log ? 19
- 20. ? 応用 – 通信速度 – 二部マッチング – DAGの最小パス被覆 – 区間グラフ – 最小カット – 最小頂点被覆 – 最大安定集合(独立集合) 20 最大流?最小費用流
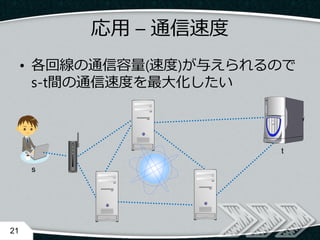
- 21. 応用 – 通信速度 ? 各回線の通信容量(速度)が与えられるので s-t間の通信速度を最大化したい 21 s t
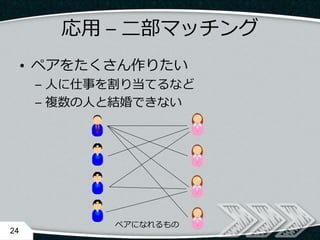
- 22. 応用 – 通信速度 ? 各回線の通信容量が与えられるので 通信速度を最大化したい – 無向グラフの場合は双方向に辺を張れば良い 22 cap cap cap
- 23. 応用 – 通信速度 ? 回線利用料がかかる場合は最小費用流 23
- 24. 応用 – 二部マッチング ? ペアをたくさん作りたい – 人に仕事を割り当てるなど – 複数の人と結婚できない 24 ペアになれるもの
- 25. 応用 – 二部マッチング ? ペアをたくさん作りたい – 以下のグラフで最大流を求めれば良い 25 s t 全て容量 1
- 26. 応用 – 二部マッチング ? ペアを作るのに異なるコストがかかる 場合は最小費用流 26
- 27. 応用 – DAGの最小パス被覆 ? グラフをいくつかの独立したパスで 被覆したい ? パス数を最小化したい 27 1 3 4 5 2
- 28. 応用 – DAGの最小パス被覆 ? 二部マッチングに帰着できる 自分の次の頂点をどれにするか (頂点数) – (最大流) が答え 28 1 3 4 5 2 s t 1 2 3 4 5 1 2 3 4 5
- 29. 応用 – 区間グラフ ? 重み付きの区間 ?, ? , ?, ? ∈ ? がいくつかあり, 重なる区間がK以下になるように区間を選び 重みの和を最大化したい – 0 → 6 に最小費用流を流量Kだけ流す 29 0 6431 2 5 ∞, 0 ∞, 0 ∞, 0 ∞, 0 ∞, 0 ∞, 0 1,-4 1,-9 1,-2 1,-3 cap, cost
- 30. 応用 – 区間グラフ ? 最小費用流において, 初期状態で 負の辺がある場合 – 初回のみBellman-Fordしてポテンシャル計算 ? 負の閉路がある場合 – 検出して予め目一杯流す 30
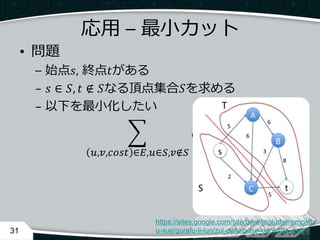
- 31. 応用 – 最小カット ? 問題 – 始点?, 終点?がある – ? ∈ ?, ? ? ?なる頂点集合?を求める – 以下を最小化したい ?,?,???? ∈?,?∈?,??? ???? 31 https://sites.google.com/site/beiwangludememo/sh u-xue/gurafu-li-lun/zui-dafuro-zui-xiaokatto-ding-li
- 32. 応用 – 最小カット ? 問題 – 別の言い方をすれば ? ? ?パスが存在しなくなるように いくつか辺をカットする – カットするのにそのコストがかかる 32 https://sites.google.com/site/beiwangludememo/sh u-xue/gurafu-li-lun/zui-dafuro-zui-xiaokatto-ding-li
- 33. 最大流?最小カット定理 33 ? 最大流 = 最小カット – 最大流 → 最小カット と変換することも 最小カット → 最大流 と変換することもある
- 35. 最大流?最小カット定理 35 ? 証明2 (理解しておくと最小カットの場所もわかる) – 最大流を流した残余グラフにおいて, sから到達可能な頂点集合を?とし, ? = ?＼Sとすると, ? ∈ ?, ? ∈ ?. – ? → ?の辺にはめいいっぱい流れていて ? → ?の辺には全く流れていない.
- 36. 最大流?最小カット定理 36 ? 証明2 – これは1つのカットだから 最小カット ≤ 最大流 TS 最大流 = 辺の合計容量 = カット(のサイズ)
- 37. 最大流?最小カット定理 37 ? 証明2 – 最小カット < 最大流 なるカット?′が 存在したとすると矛盾 T'S' 最大流 ≤ 辺の合計容量 = 最小カット
- 38. 応用 – 最小頂点被覆 ? 問題 – 無向グラフが与えられる – 頂点集合?を求める – 全ての辺 ?, ? について ? ∈ ? または ? ∈ ? でなければならない – ? のサイズを最小化したい 38
- 39. 応用 – 最小頂点被覆 ? 一般グラフの場合 最小頂点被覆の頂点数 ≥ 最大マッチングのサイズ ? 証明 – 最大マッチングの各辺に接続する頂点の一方は 少なくとも被覆されていなければならない – ≠ な例 (最小頂点被覆2, 最大マッチング1) 39 1 32
- 40. 応用 – 最小頂点被覆 ? 二部グラフの場合 最小頂点被覆の頂点数 = 最大マッチングのサイズ ? 証明 – 最小カットに帰着できる 40 全てコスト1 s t
- 41. 応用 – 最小頂点被覆 ? 証明 – 最小カットに帰着できる ??? なぜか – 最小カットが求まったとする – 下の例では赤い辺を3つ切るのが最小カット 41 全てコスト1 s t
- 42. 応用 – 最小頂点被覆 ? 証明 – カットされる辺が ? か ? に接続していると仮定する – 接続する ?, ? でないもう一方の頂点を選ぶと 頂点被覆になっている 42 s t
- 43. 応用 – 最小頂点被覆 ? 証明 – なぜか – B – D 間に枝がないことを示せばよい – あったとすると, カットではない – つまりこれは頂点被覆になっている 43 A B B C D D s t A
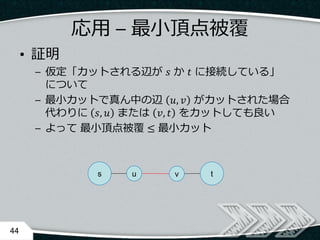
- 44. 応用 – 最小頂点被覆 ? 証明 – 仮定「カットされる辺が ? か ? に接続している」 について – 最小カットで真ん中の辺 ?, ? がカットされた場合 代わりに ?, ? または ?, ? をカットしても良い – よって 最小頂点被覆 ≤ 最小カット 44 us tv
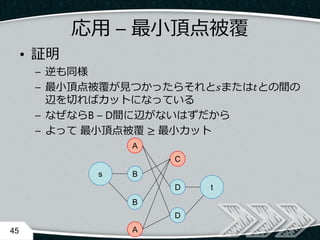
- 45. 応用 – 最小頂点被覆 ? 証明 – 逆も同様 – 最小頂点被覆が見つかったらそれと?または?との間の 辺を切ればカットになっている – なぜならB – D間に辺がないはずだから – よって 最小頂点被覆 ≥ 最小カット 45 A B B C D D s t A
- 46. 応用 – 最大安定集合(独立集合) ? 安定集合(独立集合) – どの2点間にも辺がない頂点集合 ? 最大独立集合(安定集合) は 最小頂点被覆 の補集合 46
- 47. 線形計画問題 min ? ? ? ?. ?. ?? ≤ ? 47 min 4 ?2 10 ? ?1 ?2 ?3 ?. ?. 1 6 8 4 2 5 ?1 ?2 ?3 ≤ 3 5 例
- 48. ? 主問題の最適解 = 双対問題の最適解 線形計画問題 max ? ? ? ?. ?. ?? ≤ ?, ? ≥ 0 48 min ? ? ? ?. ?. ? ? ? ≥ ?, ? ≥ 0
- 49. 線形計画問題 ? 最短経路問題 49 min 10 3 5 ? ?1 ?2 ?3 ?. ?. ?1 ?1 0 0 1 ?1 1 0 1 ?1 ?2 ?3 ≥ ?1 0 1 , ?? ≥ 0 t s 3 5 10 ?1 ?2 ?3
- 50. 線形計画問題 ? 最短経路問題 (双対) 50 t s v3 5 10 ?1 ?2 ?3 max ?1 0 1 ? ?? ? ? ?? ?. ?. ?1 0 1 ?1 1 0 0 ?1 1 ?? ? ? ?? ≤ 10 3 5
- 51. 線形計画問題 ? 最短経路問題 (双対) – 決定変数 ? ? ? ∈ ? をポテンシャルという – 1つは適当に決めて良いので ?? = 0 とする 51 ?? ? ?? ? ? ? ? ? ≤ ? ? ??? ??? ? = ?, ? ∈ ? ??? ?. ?.
- 52. 線形計画問題 ? つまり, 差分制約の最大化問題は 双対をとれば最短経路問題になる！ ? もちろん逆もできる 52