Kobe.R #18: 本の紹介: 通称「緑本」
- 2. 背景
- 4. 背景 Kobe.R の印象(参加前) ? R 専门家が自慢の业を竞い合う场
- 5. 背景 Kobe.R の印象(参加前) ? R 専门家が自慢の业を竞い合う场 ? きびしい勉強会
- 6. 背景 Kobe.R の印象(参加前) ? R 専门家が自慢の业を竞い合う场 ? きびしい勉強会 ? こわそう
- 7. 背景 Kobe.R の印象(参加前) ? R 専门家が自慢の业を竞い合う场 ? きびしい勉強会 ? こわそう
- 8. 背景 Kobe.R の印象(参加前) ? R 専门家が自慢の业を竞い合う场 ? きびしい勉強会 ? こわそう Kobe.R の印象(参加後)
- 9. 背景 Kobe.R の印象(参加前) ? R 専门家が自慢の业を竞い合う场 ? きびしい勉強会 ? こわそう Kobe.R の印象(参加後) ? そんなことはなかった
- 10. 背景 Kobe.R の印象(参加前) ? R 専门家が自慢の业を竞い合う场 ? きびしい勉強会 ? こわそう Kobe.R の印象(参加後) ? そんなことはなかった ? 以外と「どうしていいのか分からない人」が多い
- 11. 背景 Kobe.R の印象(参加前) ? R 専门家が自慢の业を竞い合う场 ? きびしい勉強会 ? こわそう Kobe.R の印象(参加後) ? そんなことはなかった ? 以外と「どうしていいのか分からない人」が多い ? R の使い方に困っているわけではない
- 12. 背景 Kobe.R の印象(参加前) ? R 専门家が自慢の业を竞い合う场 ? きびしい勉強会 ? こわそう Kobe.R の印象(参加後) ? そんなことはなかった ? 以外と「どうしていいのか分からない人」が多い ? R の使い方に困っているわけではない ? 手法の選択に困っている
- 13. 背景 Kobe.R の印象(参加前) ? R 専门家が自慢の业を竞い合う场 ? きびしい勉強会 ? こわそう Kobe.R の印象(参加後) ? そんなことはなかった ? 以外と「どうしていいのか分からない人」が多い ? R の使い方に困っているわけではない ? 手法の選択に困っている ? e.g. 弁当屋の販売数予測
- 14. 通称「緑本」
- 15. 通称「緑本」 ? 著者 ? 久保拓也(北大) ? ウミガメ上陸数のベイズ統計モデリ ング ? エゾアカヤマアリ敵対性実験の統計モ デリング ? タイトル ? データ解析のための統計モデリング入 門 — 一般化線形モデル?階層ベイズモ デル?MCMC (確率と情報の科学) ? 出版社 ? 岩波書店 ? ISBN ? 978-4-00-006973-1 ? 定価 ? 本体 3,800 円 + 税
- 16. Outline 緑本の概要 ? 本書が解説している範囲 ? おすすめポイント ? 対象読者 緑本が解説している内容 ? モデル選択の基本と GLM まで ? (GLMM 以降は次回以降に)
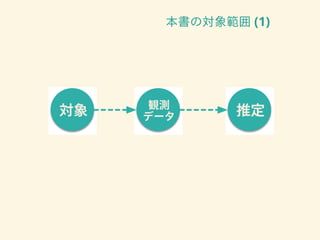
- 17. 本書の対象範囲 (1)
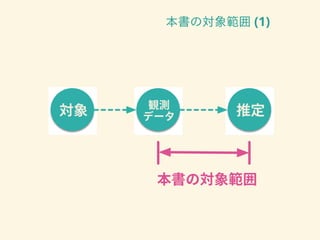
- 18. 本書の対象範囲 (1)
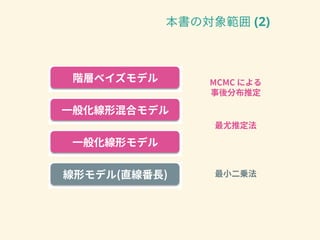
- 19. 本書の対象範囲 (2)
- 20. おすすめポイント
- 22. おすすめポイント 学部生向け ? 高校数学 ? 統計の初歩 例が身近 ? 架空の植物 ? 特定分野の知識不要
- 23. おすすめポイント 学部生向け ? 高校数学 ? 統計の初歩 例が身近 ? 架空の植物 ? 特定分野の知識不要 R の実例 ? 本書で使用するデータはダウンロード可 ? 自分で試してみることができる
- 24. Checkpoint 1
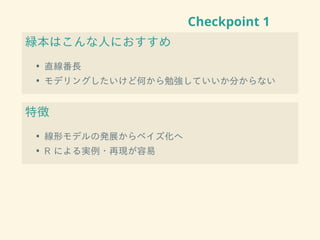
- 25. Checkpoint 1 緑本はこんな人におすすめ ? 直線番長 ? モデリングしたいけど何から勉強していいか分からない 特徴 ? 線形モデルの発展からベイズ化へ ? R による実例?再現が容易
- 26. Checkpoint 1 緑本はこんな人におすすめ ? 直線番長 ? モデリングしたいけど何から勉強していいか分からない 特徴 ? 線形モデルの発展からベイズ化へ ? R による実例?再現が容易 ではない ? 統計を学ぶために最初に手に取る ? R プログラミングを学びたい
- 27. 统计モデリングとは?
- 28. 统计モデリングとは?
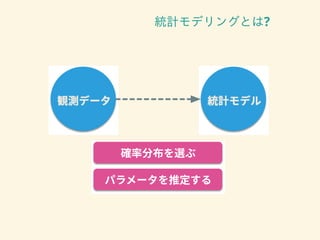
- 29. 確率分布を選ぶ 離散か連続か ? ポアソン分布?二項分布 ? 正規分布?ガンマ分布 範囲 ? 0 以上、上限とくになし ? {0, ..., N} 分散と平均との関係 ? 分散 ≈ 平均 ? 分散は平均の関数
- 30. パラメータを推定する ポワソン分布 p(y|λ) = λy exp(?λ) y! (1) ? 平均が λ であるときにポワソン分布に従う確率変数の値が y となる確率
- 31. パラメータを推定する ポワソン分布 p(y|λ) = λy exp(?λ) y! (1) ? 平均が λ であるときにポワソン分布に従う確率変数の値が y となる確率 ポワソン分布のパラメータ 平均 λ が唯一のパラメータ
- 32. 一般化線形モデル 種子数 y がポワソン分布に従う架空植物の例 ? 平均 λ ? 説明変数 xi ( x1i , x2i , . . . ) ? たとえば、植物の大きさ、施肥処理したかどうか、など ? 応答変数 y は平均 λ のポワソン分布に従う ? すなわち、「ある個体 i の平均種子数が λi 」 一般化線形モデルの二つの特徴 logλi = β0 + β1x1i + β2x2i + · · · (2) ? 左辺の log . . . リンク関数 ? 右辺 . . . 線形予測子
- 33. リンク関数と線形予測子 logλi = β0 + β1x1i + β2x2i + · · · (3) なぜ log をとるの? ? 右辺の線形予測子が負になっても λ は負にならない ? わかりやすい(和→積)、計算しやすい(積→和) パラメータ推定 ? λ の推定 → β0, β1, · · · の推定 ? 最尤推定値を探せばよい
- 34. 最尤推定
- 36. 最尤推定 緑本の展開 ? きちんと尤度の説明から対数尤度の最大化まで式を導出しな がら解説 実務的には ? R の glm 関数におまかせ ? 標準でついてきます ? くわしくは help(glm) > fit <- glm(y ~ x, data = d, family = poisson) リンク関数を指定しなければ glm 関数が正準リンク関数として対 数リンク関数(デフォルト)を使用
- 37. モデルのあてはまりのよさ 観測されたデータを全て説明変数に使えばよい? logλi = β0 + β1x1i + β2x2i + · · · (4) logλi = β0 + β1x1i (5)
- 38. モデルのあてはまりのよさ 観測されたデータを全て説明変数に使えばよい? logλi = β0 + β1x1i + β2x2i + · · · (4) logλi = β0 + β1x1i (5) 緑本の展開 最大対数尤度 → 逸脱度 (deviance) → AIC
- 39. モデルのあてはまりのよさ 観測されたデータを全て説明変数に使えばよい? logλi = β0 + β1x1i + β2x2i + · · · (4) logλi = β0 + β1x1i (5) 緑本の展開 最大対数尤度 → 逸脱度 (deviance) → AIC 実務的には ? R の MASS パッケージの stepAIC 関数(緑本 6 章) ? いい感じに AIC 最小のモデルを選択してくれる
- 40. Checkpoint 2 GLM ? 確率分布を選んでモデルを推定 ? リンク関数と線形予測子 ? モデルのあてはまりの良さ (AIC) 実務的には ? R の glm 関数 ? R の MASS パッケージの stepAIC 関数 緑本の対応範囲 第 1 章から第 4 章まで(一部第 6 章)
- 42. おわりに 緑本の紹介 入門向けに線形モデルからベイズ化までの学習に最適 (仮)緑本快速輪講 ? 緑本 5 章以降を速いペースで読んでいきます
- 43. おわりに 緑本の紹介 入門向けに線形モデルからベイズ化までの学習に最適 (仮)緑本快速輪講 ? 緑本 5 章以降を速いペースで読んでいきます ? 2 章 / 週、 担当 2 名 / 週
- 44. おわりに 緑本の紹介 入門向けに線形モデルからベイズ化までの学習に最適 (仮)緑本快速輪講 ? 緑本 5 章以降を速いペースで読んでいきます ? 2 章 / 週、 担当 2 名 / 週 ? 各週担当者が担当範囲のレジュメを用意して説明
- 45. おわりに 緑本の紹介 入門向けに線形モデルからベイズ化までの学習に最適 (仮)緑本快速輪講 ? 緑本 5 章以降を速いペースで読んでいきます ? 2 章 / 週、 担当 2 名 / 週 ? 各週担当者が担当範囲のレジュメを用意して説明 ? 参加者が集まりそうなら開催するかも
- 46. おわりに 緑本の紹介 入門向けに線形モデルからベイズ化までの学習に最適 (仮)緑本快速輪講 ? 緑本 5 章以降を速いペースで読んでいきます ? 2 章 / 週、 担当 2 名 / 週 ? 各週担当者が担当範囲のレジュメを用意して説明 ? 参加者が集まりそうなら開催するかも ? 毎週平日夜 1 時間程度を想定
- 47. おわりに 緑本の紹介 入門向けに線形モデルからベイズ化までの学習に最適 (仮)緑本快速輪講 ? 緑本 5 章以降を速いペースで読んでいきます ? 2 章 / 週、 担当 2 名 / 週 ? 各週担当者が担当範囲のレジュメを用意して説明 ? 参加者が集まりそうなら開催するかも ? 毎週平日夜 1 時間程度を想定 ? 第一回の内容(案)
- 48. おわりに 緑本の紹介 入門向けに線形モデルからベイズ化までの学習に最適 (仮)緑本快速輪講 ? 緑本 5 章以降を速いペースで読んでいきます ? 2 章 / 週、 担当 2 名 / 週 ? 各週担当者が担当範囲のレジュメを用意して説明 ? 参加者が集まりそうなら開催するかも ? 毎週平日夜 1 時間程度を想定 ? 第一回の内容(案) ? 第 4 章までのおさらいと疑問の解決
- 49. おわりに 緑本の紹介 入門向けに線形モデルからベイズ化までの学習に最適 (仮)緑本快速輪講 ? 緑本 5 章以降を速いペースで読んでいきます ? 2 章 / 週、 担当 2 名 / 週 ? 各週担当者が担当範囲のレジュメを用意して説明 ? 参加者が集まりそうなら開催するかも ? 毎週平日夜 1 時間程度を想定 ? 第一回の内容(案) ? 第 4 章までのおさらいと疑問の解決 ? 第 5 章