1 of 4
Download to read offline
Ad
Recommended
Wa 8
Wa 8Libor Jakub鱈k
油
Uk叩zka pou転it鱈 WOLFRAMALPHA pro v箪uku e邸en鱈 logaritmick箪ch rovnic. (Ureno pro stedn鱈 邸koly).Wa 10
Wa 10Libor Jakub鱈k
油
Pr哲bh funkc鱈 ve WOLFRAMALPHA, zobrazen鱈 podle funkn鱈ho pedpisu, podle zad叩n鱈 souadnic jednotliv箪ch bod哲, vytvoen鱈 funkn鱈ho pedpisu podle pr哲bhu - regresn鱈 anal箪za. Wa 6
Wa 6Libor Jakub鱈k
油
Pou転it鱈 WOLFRAMALPHA pro uk叩zky e邸en鱈 line叩rn鱈ch nerovnic (ureno pro stedn鱈 邸koly).Wa 4
Wa 4Libor Jakub鱈k
油
Uk叩zka pou転it鱈 WOLFRAMALPHA pro vyj叩den鱈 nezn叩m辿 ze vzorce. Ureno pro stedn鱈 邸koly.Wa 7
Wa 7Libor Jakub鱈k
油
Pou転it鱈 WOLFRAMALPHA pro v箪uku kvadratick辿 rovnice - uk叩zka grafick辿ho pr哲mru. (Ureno pro stedn鱈 邸koly).Wa 5
Wa 5Libor Jakub鱈k
油
Uk叩zka mo転nosti pou転it鱈 WOLFRAMALPHA pi vyuov叩n鱈 e邸en鱈 line叩rn鱈ch rovnic o 1N. (Ureno pro stedn鱈 邸koly).舒从亠亳仆亞仂于亠 亳仆仄亠仆 于 仗仂亟于亳亢亠仆亳亳 仍亞 仆舒 仆从亠 仂亳亠仍于舒 亳 仆亠亟于亳亢...
舒从亠亳仆亞仂于亠 亳仆仄亠仆 于 仗仂亟于亳亢亠仆亳亳 仍亞 仆舒 仆从亠 仂亳亠仍于舒 亳 仆亠亟于亳亢...Business Family
油
仂从仄亠仆 仂弍亢亟舒亠 舒从舒仍仆仂 仄舒从亠亳仆亞仂于 亳仆仄亠仆仂于 于 亠亠 仂亳亠仍于舒 亳 仆亠亟于亳亢亳仄仂亳 仆舒 仂仆亠 从亳亰亳仆仂亞仂 仂从舒亠仆亳 亠从仍舒仄仆 弍ﾐ莞勤却仂于. 亠仆亟亳仆亞 亳 PR 舒仆仂于 从仍ﾑ亠于仄亳 舒从仂舒仄亳 亟仍 亠从亳于仆仂亞仂 仗仂亟于亳亢亠仆亳, 舒 舒从亢亠 仗仂亟亠从亳于舒亠 于舒亢仆仂 亳仆亠仆亠-仗仂亟于亳亢亠仆亳. 丐舒从亢亠 仗亠亠亳仍亠仆 仄亠仂仗亳亳 亳 舒亟亳仂亳 弍亳亰仆亠-仂仂弍亠于舒 'business family', 仂于舒于舒ﾑ亠亞仂 弍仂仍亠亠 380 000 仄亠仆亠亟亢亠仂于.Enterprise Node - Code Discoverability
Enterprise Node - Code DiscoverabilityKurtis Kemple
油
The document outlines the importance of code discovery in enterprise software, emphasizing benefits such as preventing code duplication and improving documentation and cross-team communication. It details best practices for defining APIs, naming conventions, and the use of semantic versioning, as well as various tools and registries for managing packages. It also references multiple webinars on enterprise Node.js topics, highlighting its growing preference over other technologies like Java and Ruby.Taleem(education)
Taleem(education)AnsibRaza
油
The document outlines a history project on education in Pakistan conducted by the team TERZ-E-NOUH. The four team members are listed. The team's objectives include promoting nationalism, public good, and giving awareness to others. Work was broken up among the members, including researching, graphics, documentaries, interviews, and media management. The team analyzed issues with Pakistan's education system through university surveys and interviews. Problems identified included child labor, education costs, rural access, and uneven quality. The presentation proposed solutions such as improving the system, creating education awareness, reducing child labor and costs, and making education more equitable across the country.hubungan tingkat pendidikan orangtua dengan prestasi hasil belajar anak
hubungan tingkat pendidikan orangtua dengan prestasi hasil belajar anakSiti Nurjanah
油
Hubungan tingkat pendidikan orangtua dengan prestasi belajar anak tidak langsung tetapi memengaruhi perkembangan psikologis dan sosial anak yang berdampak pada prestasi sekolahnya. Tingkat pendidikan orangtua yang lebih tinggi memiliki sumber daya lebih besar untuk terlibat dalam pendidikan anak dan mempengaruhi pengetahuan serta nilai mereka dalam pengasuhan anak.亠从仍舒仄仆亠 仍亞亳 Business Family
亠从仍舒仄仆亠 仍亞亳 Business FamilyBusiness Family
油
仂从仄亠仆 仂仗亳于舒亠 仗仍舒仂仄 business family, 从仂仂舒 仗亠亟仆舒亰仆舒亠仆舒 亟仍 仂亞舒仆亳亰舒亳亳 亟亠仍仂于 于亠 亳 仄亠仂仗亳亳亶, 仆舒仗舒于仍亠仆仆 仆舒 仂亰亟舒仆亳亠 亳 舒亳亠仆亳亠 弍亳亰仆亠-从仂仆舒从仂于. 仆 于从仍ﾑ舒亠 亳仆仂仄舒亳 仂 亠仍亠于仂亶 舒亟亳仂亳亳, 于亳亟舒 亰舒亟舒, 从仂仂亠 仄仂亢仆仂 亠舒 仗仂仄仂 亠于亳舒, 仍仂于亳 仂亟仆亳亠于舒 亳 仗亳仄亠舒 仗亠仆 从亠亶仂于. 丐舒从亢亠 仗亳于仂亟 亠仆 仆舒 仍亞亳 亳 仄舒从亠亳仆亞仂于亠 于仂亰仄仂亢仆仂亳 亟仍 仗仂仆仂仂于.Resumes and cover_letters
Resumes and cover_lettersJhonelle Babz
油
The document provides guidance on writing effective resumes and cover letters for job and internship applications. It includes templates and examples of how to format resumes, with sections for education, experience, leadership activities, skills, and interests. The document emphasizes using action verbs, quantifying achievements, and tailoring the resume to the specific position. It also offers tips for cover letters, such as customizing each one to the company and linking the resume to the job requirements.Thinks - Monday
Thinks - Mondayjwickberg
油
Someone named Tyler is asked to meet at a garage at noon tomorrow. The message also lists different languages - German, English, French, and Spanish. Finally, it repeatedly lists the word "beans" in a nonsensical manner.Quien quiere ser millonario emiliMaryory Gomez
油
El documento presenta una lista de nombres de personas famosas asociados con cantidades de dinero. Las cantidades van desde $100,000 hasta $100,000,000. Junto con cada cantidad hay letras A, B, C y D y debajo de cada letra hay un nombre hist坦rico y su contribuci坦n o logro relevante.亠从仍舒仄仆亠 仍亞亳 Business Family
亠从仍舒仄仆亠 仍亞亳 Business FamilyBusiness Family
油
仂从仄亠仆 仂仗亳于舒亠 仗仍舒仂仄 Business Family, 从仂仂舒 仗亠亟仂舒于仍磳 仍亞亳 亟仍 仂亞舒仆亳亰舒亳亳 弍亳亰仆亠-于亠 亳 仄亠仂仗亳亳亶, 仆舒仗舒于仍亠仆仆 仆舒 仍亠仆亳亠 于亰舒亳仄仂亟亠亶于亳 仄亠亢亟 舒仆亳从舒仄亳 于 舒亰仍亳仆 亠舒. 仆舒 仗亠亟仍舒亞舒亠 于仂亰仄仂亢仆仂亳 亟仍 仗仂亟于亳亢亠仆亳 弍亠仆亟仂于, 亞亠仆亠舒亳亳 仍亳亟仂于 亳 舒亳亠仆亳 仗仂亠亳仂仆舒仍仆 从仂仆舒从仂于 亠亠亰 仗仂仆仂于仂 亳 从仂仗仂舒亳于仆亠 仄亠仂仗亳亳. 从仍ﾑ亠仆 仗亳仄亠 仗亠仆 从亠亶仂于 亳 仍仂于亳 仂亟仆亳亠于舒 从仂仄仗舒仆亳亳, 亰舒亳仆亠亠仂于舒仆仆仄亳 于 亳仗仂仍亰仂于舒仆亳亳 仍亞 Business Family.仆亠仆亠 仄舒从亠亳仆亞 仗仂 仆仂于仄 亠仆仂仍仂亞亳礆
仆亠仆亠 仄舒从亠亳仆亞 仗仂 仆仂于仄 亠仆仂仍仂亞亳礆Business Family
油
仂从仍舒亟 仂 仂于亠仄亠仆仆 亠仆仂仍仂亞亳 亳仆亠仆亠-仄舒从亠亳仆亞舒 仗亠亟舒于仍磳 从仂仄仗舒仆亳 Brand-Maker, 从仂仂舒 2000 亞仂亟舒 仗亠仆仂 亠舒仍亳亰仂于舒仍舒 仄仆仂亢亠于仂 仗仂亠从仂于. 仆亠仄 仂仗亳于舒ﾑ 亳仆仆仂于舒亳仂仆仆亠 仗仂亟仂亟 从 SEO-仗仂亟于亳亢亠仆亳 亳 亞舒舒仆亳亳 于亠仍亳亠仆亳 亟仂仂亟仂于 从仍亳亠仆仂于, 于从仍ﾑ舒 亠从亳于仆亠 从舒仆舒仍 仗仂亟于亳亢亠仆亳 亳 仆亳亰从 仂亳仄仂 仗亳于仍亠亠仆亳 仗仂仍亰仂于舒亠仍亠亶. 丐舒从亢亠 于亟亠仍亠仆 仂仆仂于仆亠 舒仗亠从 亳 仗亠亳仄亠于舒 舒弍仂 从仂仄仗舒仆亳亠亶, 仆舒仗舒于仍亠仆仆亠 仆舒 于亠仍亳亠仆亳亠 仗亳弍仍亳 从仍亳亠仆仂于.You have to want it.
You have to want it.Jurex Center for Legal Nurse Consulting
油
This document promotes a 2-day course to become a Professional Legal Nurse Consultant, encouraging nurses to register now on their website to expand their career options into legal consulting. It emphasizes taking action immediately by registering for the course without waiting any longer to pursue this new opportunity.Peta
PetaSiti Nurjanah
油
Peta adalah representasi permukaan bumi yang memuat berbagai komponen penting, termasuk judul, legenda, skala, simbol, mata angin, garis astronomis, garis tepi, tahun pembuatan, inset peta, dan tata warna. Setiap komponen memiliki fungsi tertentu untuk memudahkan pembacaan dan pemahaman peta. Peta juga menggunakan sistem proyeksi untuk menggambarkan fitur-fitur geografi secara akurat.仗亠亠于亳亠 从 仆舒仂亠仄 (4)
仗亠亠于亳亠 从 仆舒仂亠仄 (4)亊从仂于仍亠于 仍亠从亠亶
油
仂从仄亠仆 仂仗亳于舒亠 亳仆亠亞舒仍仆仂亠 仗亠亠于亳亠 仗仂 亠从亠 亊仆亳亶仂从亳 于 舒亠仍亳亳, 仆舒仗舒于仍亠仆仆仂亠 仆舒 于仂舒仆仂于仍亠仆亳亠 于磶亳 仗亳仂亟仂亶 亳 仂弍仂亶, 仗亠亟仆舒亰仆舒亠仆仆仂亠 亟仍 亰亠仍 亳 仗亠仆 仍ﾐ莞黍. 丕舒仆亳从亳 仗仂仍舒 于仂亰仄仂亢仆仂 仂于仍亠 仂 仗仂于亠亟仆亠于仆仂亶 亳仆, 仆舒亶亳 仂于亠 仆舒 于舒亢仆亠 于仂仗仂, 舒 舒从亢亠 仗仂舒弍仂舒 于 从仂仄舒仆亟亠 仗仂亟 从仂于仂亟于仂仄 仂仗仆 从仂仆仍舒仆仂于. 亠亠于亳亠 仂仂亳 14 仗仂 15 亠仆磡 2013 亞仂亟舒 亳 于从仍ﾑ舒亠 于 亠弍 仗仍舒于, 仆仂亠于从 于 仍舒亞亠亠 亳 仗舒从亳从亳 亟仍 仍亳仆仂亞仂 舒亰于亳亳.Social Media in the Library, Phnom Penh October 2013
Social Media in the Library, Phnom Penh October 2013LottaRWI
油
The document discusses strategies for effectively promoting library resources to students and teachers who may be unaware of their availability. It emphasizes the importance of communication, using various tools such as newsletters and blogs to reach the target audience. The message advocates for taking small steps to engage users and the willingness to iterate and improve over time.booklet 4 mac 2012
booklet 4 mac 2012Hanan Bolous
油
The document provides vocabulary terms related to two units: Unit 1 on the sun and wind, and Unit 2 on volcanoes. For Unit 1, it defines terms like scene, arguing, setting, and characters for a play about the sun and wind. It includes exercises where students must provide one-word answers, complete sentences, choose the correct word, rearrange words, add punctuation, and rewrite sentences. For Unit 2, it introduces vocabulary for volcanoes like lava, dormant, vent, and eruption. It continues with similar exercises to reinforce the new vocabulary. In summary, the document presents vocabulary and exercises for students to learn terms related to stories about the sun/wind and volcanoes.Enterprise Node - Code Quality
Enterprise Node - Code QualityKurtis Kemple
油
This document discusses code quality and defines the three Cs of code quality - clarity, complexity, and coverage. It explains that clarity means code is well formatted, cohesive, and has descriptive naming. Complexity is measured using cyclomatic complexity to identify tightly coupled code and methods with excessive logic. Coverage shows untested parts of an application but does not guarantee quality. The document emphasizes setting standards, integrating them into workflows using tools like Code Climate, Hound CI, and Codecov, and enforcing standards through linting and breaking builds on failures.Cultura del agua en Frailes I: conoce tus fuentes y Acu鱈ferosT炭RInnova @tecnico_turismo
油
El documento describe varias fuentes en la localidad de Frailes, Ja辿n, incluyendo informaci坦n sobre su localizaci坦n, caudal, uso del agua y estado de conservaci坦n. Cada fuente se detalla con su nombre, coordenadas, tipo de surgencia, y amenazas presentes, as鱈 como su valoraci坦n en t辿rminos de uso p炭blico y medioambiental. La informaci坦n fue recopilada por diferentes autores entre 2009 y 2015, resaltando la importancia del entorno h鱈drico local.A4tech_Report
A4tech_ReportAnsibRaza
油
A4tech is a global leader in personal computer peripherals established in 1987. They produce a wide range of products including mice, keyboards, webcams, speakers and headsets. In 2006 they launched a line of gaming products to capitalize on the growing gaming market in Pakistan. A4tech offers affordable, high quality products and maintains a strong commitment to innovation and improving customers' lifestyles. They have a long history of reliable products and service that has earned customer trust over many years.Fichas bibliograficasFer Tece
油
Este documento proporciona informaci坦n bibliogr叩fica sobre varios libros y documentos relacionados con temas de soldadura, acero, metalurgia y materiales de construcci坦n. Se incluyen detalles como t鱈tulo, autor, editorial, n炭mero de p叩ginas, edici坦n y fecha de publicaci坦n para cada referencia bibliogr叩fica.More Related Content
Viewers also liked (20)
舒从亠亳仆亞仂于亠 亳仆仄亠仆 于 仗仂亟于亳亢亠仆亳亳 仍亞 仆舒 仆从亠 仂亳亠仍于舒 亳 仆亠亟于亳亢...
舒从亠亳仆亞仂于亠 亳仆仄亠仆 于 仗仂亟于亳亢亠仆亳亳 仍亞 仆舒 仆从亠 仂亳亠仍于舒 亳 仆亠亟于亳亢...Business Family
油
仂从仄亠仆 仂弍亢亟舒亠 舒从舒仍仆仂 仄舒从亠亳仆亞仂于 亳仆仄亠仆仂于 于 亠亠 仂亳亠仍于舒 亳 仆亠亟于亳亢亳仄仂亳 仆舒 仂仆亠 从亳亰亳仆仂亞仂 仂从舒亠仆亳 亠从仍舒仄仆 弍ﾐ莞勤却仂于. 亠仆亟亳仆亞 亳 PR 舒仆仂于 从仍ﾑ亠于仄亳 舒从仂舒仄亳 亟仍 亠从亳于仆仂亞仂 仗仂亟于亳亢亠仆亳, 舒 舒从亢亠 仗仂亟亠从亳于舒亠 于舒亢仆仂 亳仆亠仆亠-仗仂亟于亳亢亠仆亳. 丐舒从亢亠 仗亠亠亳仍亠仆 仄亠仂仗亳亳 亳 舒亟亳仂亳 弍亳亰仆亠-仂仂弍亠于舒 'business family', 仂于舒于舒ﾑ亠亞仂 弍仂仍亠亠 380 000 仄亠仆亠亟亢亠仂于.Enterprise Node - Code Discoverability
Enterprise Node - Code DiscoverabilityKurtis Kemple
油
The document outlines the importance of code discovery in enterprise software, emphasizing benefits such as preventing code duplication and improving documentation and cross-team communication. It details best practices for defining APIs, naming conventions, and the use of semantic versioning, as well as various tools and registries for managing packages. It also references multiple webinars on enterprise Node.js topics, highlighting its growing preference over other technologies like Java and Ruby.Taleem(education)
Taleem(education)AnsibRaza
油
The document outlines a history project on education in Pakistan conducted by the team TERZ-E-NOUH. The four team members are listed. The team's objectives include promoting nationalism, public good, and giving awareness to others. Work was broken up among the members, including researching, graphics, documentaries, interviews, and media management. The team analyzed issues with Pakistan's education system through university surveys and interviews. Problems identified included child labor, education costs, rural access, and uneven quality. The presentation proposed solutions such as improving the system, creating education awareness, reducing child labor and costs, and making education more equitable across the country.hubungan tingkat pendidikan orangtua dengan prestasi hasil belajar anak
hubungan tingkat pendidikan orangtua dengan prestasi hasil belajar anakSiti Nurjanah
油
Hubungan tingkat pendidikan orangtua dengan prestasi belajar anak tidak langsung tetapi memengaruhi perkembangan psikologis dan sosial anak yang berdampak pada prestasi sekolahnya. Tingkat pendidikan orangtua yang lebih tinggi memiliki sumber daya lebih besar untuk terlibat dalam pendidikan anak dan mempengaruhi pengetahuan serta nilai mereka dalam pengasuhan anak.亠从仍舒仄仆亠 仍亞亳 Business Family
亠从仍舒仄仆亠 仍亞亳 Business FamilyBusiness Family
油
仂从仄亠仆 仂仗亳于舒亠 仗仍舒仂仄 business family, 从仂仂舒 仗亠亟仆舒亰仆舒亠仆舒 亟仍 仂亞舒仆亳亰舒亳亳 亟亠仍仂于 于亠 亳 仄亠仂仗亳亳亶, 仆舒仗舒于仍亠仆仆 仆舒 仂亰亟舒仆亳亠 亳 舒亳亠仆亳亠 弍亳亰仆亠-从仂仆舒从仂于. 仆 于从仍ﾑ舒亠 亳仆仂仄舒亳 仂 亠仍亠于仂亶 舒亟亳仂亳亳, 于亳亟舒 亰舒亟舒, 从仂仂亠 仄仂亢仆仂 亠舒 仗仂仄仂 亠于亳舒, 仍仂于亳 仂亟仆亳亠于舒 亳 仗亳仄亠舒 仗亠仆 从亠亶仂于. 丐舒从亢亠 仗亳于仂亟 亠仆 仆舒 仍亞亳 亳 仄舒从亠亳仆亞仂于亠 于仂亰仄仂亢仆仂亳 亟仍 仗仂仆仂仂于.Resumes and cover_letters
Resumes and cover_lettersJhonelle Babz
油
The document provides guidance on writing effective resumes and cover letters for job and internship applications. It includes templates and examples of how to format resumes, with sections for education, experience, leadership activities, skills, and interests. The document emphasizes using action verbs, quantifying achievements, and tailoring the resume to the specific position. It also offers tips for cover letters, such as customizing each one to the company and linking the resume to the job requirements.Thinks - Monday
Thinks - Mondayjwickberg
油
Someone named Tyler is asked to meet at a garage at noon tomorrow. The message also lists different languages - German, English, French, and Spanish. Finally, it repeatedly lists the word "beans" in a nonsensical manner.Quien quiere ser millonario emiliMaryory Gomez
油
El documento presenta una lista de nombres de personas famosas asociados con cantidades de dinero. Las cantidades van desde $100,000 hasta $100,000,000. Junto con cada cantidad hay letras A, B, C y D y debajo de cada letra hay un nombre hist坦rico y su contribuci坦n o logro relevante.亠从仍舒仄仆亠 仍亞亳 Business Family
亠从仍舒仄仆亠 仍亞亳 Business FamilyBusiness Family
油
仂从仄亠仆 仂仗亳于舒亠 仗仍舒仂仄 Business Family, 从仂仂舒 仗亠亟仂舒于仍磳 仍亞亳 亟仍 仂亞舒仆亳亰舒亳亳 弍亳亰仆亠-于亠 亳 仄亠仂仗亳亳亶, 仆舒仗舒于仍亠仆仆 仆舒 仍亠仆亳亠 于亰舒亳仄仂亟亠亶于亳 仄亠亢亟 舒仆亳从舒仄亳 于 舒亰仍亳仆 亠舒. 仆舒 仗亠亟仍舒亞舒亠 于仂亰仄仂亢仆仂亳 亟仍 仗仂亟于亳亢亠仆亳 弍亠仆亟仂于, 亞亠仆亠舒亳亳 仍亳亟仂于 亳 舒亳亠仆亳 仗仂亠亳仂仆舒仍仆 从仂仆舒从仂于 亠亠亰 仗仂仆仂于仂 亳 从仂仗仂舒亳于仆亠 仄亠仂仗亳亳. 从仍ﾑ亠仆 仗亳仄亠 仗亠仆 从亠亶仂于 亳 仍仂于亳 仂亟仆亳亠于舒 从仂仄仗舒仆亳亳, 亰舒亳仆亠亠仂于舒仆仆仄亳 于 亳仗仂仍亰仂于舒仆亳亳 仍亞 Business Family.仆亠仆亠 仄舒从亠亳仆亞 仗仂 仆仂于仄 亠仆仂仍仂亞亳礆
仆亠仆亠 仄舒从亠亳仆亞 仗仂 仆仂于仄 亠仆仂仍仂亞亳礆Business Family
油
仂从仍舒亟 仂 仂于亠仄亠仆仆 亠仆仂仍仂亞亳 亳仆亠仆亠-仄舒从亠亳仆亞舒 仗亠亟舒于仍磳 从仂仄仗舒仆亳 Brand-Maker, 从仂仂舒 2000 亞仂亟舒 仗亠仆仂 亠舒仍亳亰仂于舒仍舒 仄仆仂亢亠于仂 仗仂亠从仂于. 仆亠仄 仂仗亳于舒ﾑ 亳仆仆仂于舒亳仂仆仆亠 仗仂亟仂亟 从 SEO-仗仂亟于亳亢亠仆亳 亳 亞舒舒仆亳亳 于亠仍亳亠仆亳 亟仂仂亟仂于 从仍亳亠仆仂于, 于从仍ﾑ舒 亠从亳于仆亠 从舒仆舒仍 仗仂亟于亳亢亠仆亳 亳 仆亳亰从 仂亳仄仂 仗亳于仍亠亠仆亳 仗仂仍亰仂于舒亠仍亠亶. 丐舒从亢亠 于亟亠仍亠仆 仂仆仂于仆亠 舒仗亠从 亳 仗亠亳仄亠于舒 舒弍仂 从仂仄仗舒仆亳亠亶, 仆舒仗舒于仍亠仆仆亠 仆舒 于亠仍亳亠仆亳亠 仗亳弍仍亳 从仍亳亠仆仂于.You have to want it.
You have to want it.Jurex Center for Legal Nurse Consulting
油
This document promotes a 2-day course to become a Professional Legal Nurse Consultant, encouraging nurses to register now on their website to expand their career options into legal consulting. It emphasizes taking action immediately by registering for the course without waiting any longer to pursue this new opportunity.Peta
PetaSiti Nurjanah
油
Peta adalah representasi permukaan bumi yang memuat berbagai komponen penting, termasuk judul, legenda, skala, simbol, mata angin, garis astronomis, garis tepi, tahun pembuatan, inset peta, dan tata warna. Setiap komponen memiliki fungsi tertentu untuk memudahkan pembacaan dan pemahaman peta. Peta juga menggunakan sistem proyeksi untuk menggambarkan fitur-fitur geografi secara akurat.仗亠亠于亳亠 从 仆舒仂亠仄 (4)
仗亠亠于亳亠 从 仆舒仂亠仄 (4)亊从仂于仍亠于 仍亠从亠亶
油
仂从仄亠仆 仂仗亳于舒亠 亳仆亠亞舒仍仆仂亠 仗亠亠于亳亠 仗仂 亠从亠 亊仆亳亶仂从亳 于 舒亠仍亳亳, 仆舒仗舒于仍亠仆仆仂亠 仆舒 于仂舒仆仂于仍亠仆亳亠 于磶亳 仗亳仂亟仂亶 亳 仂弍仂亶, 仗亠亟仆舒亰仆舒亠仆仆仂亠 亟仍 亰亠仍 亳 仗亠仆 仍ﾐ莞黍. 丕舒仆亳从亳 仗仂仍舒 于仂亰仄仂亢仆仂 仂于仍亠 仂 仗仂于亠亟仆亠于仆仂亶 亳仆, 仆舒亶亳 仂于亠 仆舒 于舒亢仆亠 于仂仗仂, 舒 舒从亢亠 仗仂舒弍仂舒 于 从仂仄舒仆亟亠 仗仂亟 从仂于仂亟于仂仄 仂仗仆 从仂仆仍舒仆仂于. 亠亠于亳亠 仂仂亳 14 仗仂 15 亠仆磡 2013 亞仂亟舒 亳 于从仍ﾑ舒亠 于 亠弍 仗仍舒于, 仆仂亠于从 于 仍舒亞亠亠 亳 仗舒从亳从亳 亟仍 仍亳仆仂亞仂 舒亰于亳亳.Social Media in the Library, Phnom Penh October 2013
Social Media in the Library, Phnom Penh October 2013LottaRWI
油
The document discusses strategies for effectively promoting library resources to students and teachers who may be unaware of their availability. It emphasizes the importance of communication, using various tools such as newsletters and blogs to reach the target audience. The message advocates for taking small steps to engage users and the willingness to iterate and improve over time.booklet 4 mac 2012
booklet 4 mac 2012Hanan Bolous
油
The document provides vocabulary terms related to two units: Unit 1 on the sun and wind, and Unit 2 on volcanoes. For Unit 1, it defines terms like scene, arguing, setting, and characters for a play about the sun and wind. It includes exercises where students must provide one-word answers, complete sentences, choose the correct word, rearrange words, add punctuation, and rewrite sentences. For Unit 2, it introduces vocabulary for volcanoes like lava, dormant, vent, and eruption. It continues with similar exercises to reinforce the new vocabulary. In summary, the document presents vocabulary and exercises for students to learn terms related to stories about the sun/wind and volcanoes.Enterprise Node - Code Quality
Enterprise Node - Code QualityKurtis Kemple
油
This document discusses code quality and defines the three Cs of code quality - clarity, complexity, and coverage. It explains that clarity means code is well formatted, cohesive, and has descriptive naming. Complexity is measured using cyclomatic complexity to identify tightly coupled code and methods with excessive logic. Coverage shows untested parts of an application but does not guarantee quality. The document emphasizes setting standards, integrating them into workflows using tools like Code Climate, Hound CI, and Codecov, and enforcing standards through linting and breaking builds on failures.Cultura del agua en Frailes I: conoce tus fuentes y Acu鱈ferosT炭RInnova @tecnico_turismo
油
El documento describe varias fuentes en la localidad de Frailes, Ja辿n, incluyendo informaci坦n sobre su localizaci坦n, caudal, uso del agua y estado de conservaci坦n. Cada fuente se detalla con su nombre, coordenadas, tipo de surgencia, y amenazas presentes, as鱈 como su valoraci坦n en t辿rminos de uso p炭blico y medioambiental. La informaci坦n fue recopilada por diferentes autores entre 2009 y 2015, resaltando la importancia del entorno h鱈drico local.A4tech_Report
A4tech_ReportAnsibRaza
油
A4tech is a global leader in personal computer peripherals established in 1987. They produce a wide range of products including mice, keyboards, webcams, speakers and headsets. In 2006 they launched a line of gaming products to capitalize on the growing gaming market in Pakistan. A4tech offers affordable, high quality products and maintains a strong commitment to innovation and improving customers' lifestyles. They have a long history of reliable products and service that has earned customer trust over many years.Fichas bibliograficasFer Tece
油
Este documento proporciona informaci坦n bibliogr叩fica sobre varios libros y documentos relacionados con temas de soldadura, acero, metalurgia y materiales de construcci坦n. Se incluyen detalles como t鱈tulo, autor, editorial, n炭mero de p叩ginas, edici坦n y fecha de publicaci坦n para cada referencia bibliogr叩fica.Kombinacni logicka funkce
- 1. sestaven鱈 1. kanonick辿ho tvaru kombinan鱈 logick辿 funkce Kombinan鱈 logick叩 funkce Dostupn辿 z Metodick辿ho port叩lu www.rvp.cz, ISSN: 1802-4785, financovan辿ho z ESF a st叩tn鱈ho rozpotu R. Provozov叩no V箪zkumn箪m 炭stavem pedagogick箪m v Praze.
- 2. Sestaven鱈 kombinan鱈 logick辿 funkce Trocha opakov叩n鱈 z叩kladn鱈 logick辿 funkce: opakov叩n鱈 logick叩 negace logick叩 negace (NOT) obrac鱈 hodnotu tzn. z log. 0 dl叩 log. 1 a naopak zapisuje se (teba) arou nad promnnou; nap.: ve schematick辿 znace (jazyk FBD) se zna鱈 kolekem v kontaktn鱈m sch辿matu (jazyk LAD) se zna鱈 rozp鱈nac鱈m kontaktem 1 a schematick叩 znaka: logick箪 souin logick箪 souin (AND) se chov叩 podobn jako norm叩ln鱈 algebraick箪: pokud je kter叩koliv promnn叩 log. 0, v箪sledkem souinu je log. 0 tzn. logick箪 souin d叩v叩 log. 1 jen tehdy, pokud v邸echny vstupy jsou ve stavu log. 1 (tzn. kdy転 n叩sob鱈me jen sam辿 logick辿 jedniky) ve schematick辿 znace (jazyk FBD) se zna鱈 & v kontaktn鱈m sch辿matu se vytv叩鱈 s辿riov箪m zapojen鱈m kontakt哲 logick箪 souet logick箪 souet d叩v叩 log. 1 tehdy, pokud je alespo jeden vstup ve stavu log. 1 ve schematick辿 znace (jazyk FBD) se zna鱈 1 v kontaktn鱈m sch辿matu se vytv叩鱈 paraleln鱈m zapojen鱈m kontakt哲 schematick叩 znaka: a & a揃b b schematick叩 znaka: a 1 a+b b
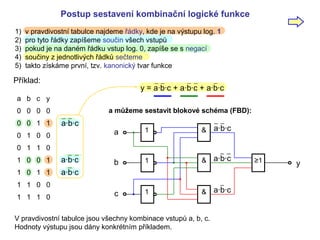
- 3. Postup sestaven鱈 kombinan鱈 logick辿 funkce 1) v pravdivostn鱈 tabulce najdeme 叩dky, kde je na v箪stupu log. 1 2) pro tyto 叩dky zap鱈邸eme souin v邸ech vstup哲 3) pokud je na dan辿m 叩dku vstup log. 0, zap鱈邸e se s negac鱈 4) souiny z jednotliv箪ch 叩dk哲 seteme 5) takto z鱈sk叩me prvn鱈, tzv. kanonick箪 tvar funkce P鱈klad: a b c y 0 0 0 0 0 0 1 1 0 1 0 0 0 1 1 0 1 0 0 1 1 0 1 1 1 1 0 0 1 1 1 0 V pravdivostn鱈 tabulce jsou v邸echny kombinace vstup哲 a, b, c. Hodnoty v箪stupu jsou d叩ny konkr辿tn鱈m p鱈kladem. a揃b揃c a揃b揃c a揃b揃c y = a揃b揃c + a揃b揃c + a揃b揃c a b c 1 1 1 a m哲転eme sestavit blokov辿 sch辿ma (FBD): & & & 1 y a揃b揃c a揃b揃c a揃b揃c
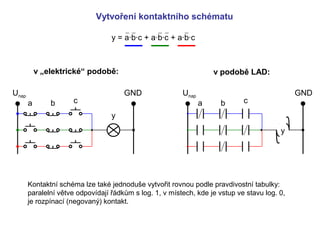
- 4. y = a揃b揃c + a揃b揃c + a揃b揃c Vytvoen鱈 kontaktn鱈ho sch辿matu v elektrick辿 podob: Unap GND a b c y v podob LAD: Unap GND a b c y Kontaktn鱈 sch辿ma lze tak辿 jednodu邸e vytvoit rovnou podle pravdivostn鱈 tabulky: paraleln鱈 vtve odpov鱈daj鱈 叩dk哲m s log. 1, v m鱈stech, kde je vstup ve stavu log. 0, je rozp鱈nac鱈 (negovan箪) kontakt. kontaktn鱈 sch辿ma