Kuantor dan Validitas Pembuktian
- 1. Oleh : Emanueli Mendrofa, S.Pd Mata Kuliah : Teori Himpunan dan Logika Matematika
- 2. Fungsi Pernyataan Definisi: Suatu fungsi pernyataan adalah suatu kalimat terbuka di dalam semesta pembicaraan (semesta pembicaraan diberikan secara eksplisit atau implisit). Fungsi pernyataan merupakan suatu kalimat terbuka yang ditulis sebagai p(x) yang bersifat bahwa p(x) bernilai benar atau salah (tidak keduanya) untuk setiap x (x adalah anggota dari semesta pembicaraan). Ingat bahwa p(x) suatu pernyataan.
- 3. Contoh: 1. Jika p(x) = 1 + x > 5 p(x) akan merupakan fungsi pernyataan pada A = himpunan bilangan asli. Karena demikian maka p(x) bernilai benar untuk x = 5, 6, 7, . . . 2. Jika q(x) = x + 3 < 1 didefinisikan pada A = himpunan bilangan asli, tidak ada x yang menyebabkan q(x) bernilai benar.
- 4. Kuantor Umum (Kuantor Universal) Simbol ’Ćó yang dibaca ŌĆ£untuk semuaŌĆØ atau ŌĆ£untuk setiapŌĆØ disebut kuantor umum. Jika p(x) adalah fungsi proposisi pada suatu himpunan A (himpunan A adalah semesta pembicaraannya) maka: ’Ćóx ’āÄ A, p(x) dibaca untuk semua x elemen A berlakulah p(x) ’Ćóx, p(x) atau ’Ćóx p(x) dibaca untuk semua x
- 5. Contoh: 1. p(x) = x tidak kekal p(manusia) = Manusia tidak kekal maka ’Ćóx, p(x) = ’Ćóx ’āÄ {manusia}, p(x) = semua manusia tidak kekal (Benar) Perhatikan bahwa p(x) merupakan kalimat terbuka (tidak mempunyai nilai kebenaran). Tetapi ’Ćóx p(x) merupakan pernyataan (mempunyai nilai benar atau salah tetapi tidak kedua-duanya). 11.p(x) = Semua mahasiswa IKIP Gunungsitoli pandai (Benar) berarti: semua (tanpa terkecuali) mahasiswa IKIP
- 6. Kuantor Khusus (Kuantor Eksistensial) Simbol ’Ćż dibaca ŌĆ£adaŌĆØ atau ŌĆ£untuk beberapaŌĆØ atau ŌĆ£untuk paling sedikit satuŌĆØ disebut kuantor khusus. Jika p(x) adalah fungsi pernyataan pada himpunan tertentu yaitu A (himpunan A adalah semesta pembicaraan) maka: ’Ćżx ’āÄ A, p(x) dibaca ada x elemen A, sedemikian hingga p(x) ’Ćżx! p(x) atau ’Ćżx, p(x) atau ’Ćżx p(x) dibaca untuk
- 7. Contoh: 1. p(x) = x adalah wanita p(perwira ABRI) = Perwira ABRI adalah wanita ’Ćżx p(x) = ’Ćżx! p(x) = ’Ćżx ’āÄ {perwira ABRI}, p(x) = ada perwira ABRI adalah wanita (Benar) 11.Misalkan: A= Himpunan Semua Mahasiswa IKIP Gunungsitoli B= Beberapa Mahasiswa IKIP Gunungsitoli pandai berarti: ada Mahasiswa IKIP Gunungsitoli yang pandai atau sekurang-kurangya ada seorang Mahasiswa IKIP Gunungsitoli yang pandai.
- 8. Negasi Suatu Pernyatan yang Mengandung Kuantor Negasi dari: Semua manusia tidak kekal = Atau: Semua manusia tidak kekal = Jika p(x) adalah manusia tidak kekal atau x tidak kekal, maka ŌĆ£Semua manusia adalah tidak kekalŌĆØ atau ’Ćóx, p(x) bernilai benar, dan ŌĆ£Beberapa manusia kekalŌĆØ atau ’Ćżx, ~p(x) bernilai salah. Pernyataan di atas dapat dituliskan dengan simbol: ~ [’Ćóx p(x)] ’é║ ’Ćżx ~p(x) Tidak benar bahwa semua manusia tidak kekal Beberapa manusia kekal
- 9. Jadi negasi dari suatu pernyataan yang mengandung kuantor universal adalah ekivalen dengan pernyataan yang mengandung kuantor eksistensial (fungsi pernyataan yang dinegasikan) dan sebaliknya : ~[’Ćżx p(x)] ’é║ ’Ćóx ~p(x) Contoh: p : ~p : q : ~q : r : ~r : ~r : Semua mahasiswa rajin belajar Ada mahasiswa yang tidak rajin belajar Ada mahasiswa yang rumahnya di Lahewa Semua mahasiswa rumahnya bukan di Lahewa Jika semua mahasiswa rajin belajar maka lulus ujianSemua mahasiswa rajin belajar dan tidak lulus ujianSemua mahasiswa rajin belajar tetapi tidak lulus ujian
- 11. Premis dan Argumen Premis adalah pernyataan-pernyataan yang digunakan untuk menarik suatu kesimpulan. Suatu premis dapat berupa aksioma, hipotesa, definisi atau pernyataan yang sudah dibuktikan sebelumnya. Sedangkan argumen adalah kumpulan kalimat yang terdiri atas satu atau lebih premis yang mengandung bukti-bukti (evidence) dan suatu (satu) konklusi. Secara sederhana dapat dikatakan bahwa suatu argumen dikatakan sah/valid jika premis-premisnya benar, maka konklusinya juga benar.
- 12. Validitas Pembuktian atau Penarikan Kesimpulan Dalam penarikan kesimpulan biasanya menggunakan prinsip logika dimana pernyataan disebut premis serta penarikan kesimpulan disebut argumentasi. Prinsip logika bila premis- premisnya benar maka konklusinya sah atau valid. Sebaliknya jika premis-premisnya salah maka konklusinya tidak sah atau tidak valid.
- 14. Modus Ponen Dalam bentuk implikasi pernyataan penarikan kesimpulan dengan modus ponen ditulis: {(p ŌćÆ q) Ōł¦ p} ŌćÆ q dibaca ŌĆ£implikasi dikonjungsikan dengan p berimplikasi (menghasilkan) kesimpulan atau konklusi q. Uraian modus ponen dapat ditulis: Premis 1 : Premis 2 : Konklusi : Uraian di atas dapat juga dibaca: Apabila diketahui jika p maka q benar, dan p benar, disimpulkan q benar. (Notasi: Ada yang menggunakan tanda ’ü£ untuk menyatakan konklusi, seperti p ŌćÆ q, p’ü£q) p ŌćÆ q p q
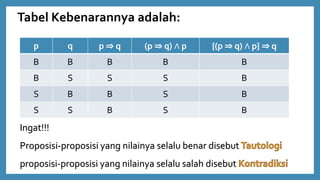
- 15. Tabel Kebenarannya adalah: p q p ŌćÆ q (p ŌćÆ q) Ōł¦ p {(p ŌćÆ q) Ōł¦ p} ŌćÆ q B B B B B B S S S B S B B S B S S B S B Ingat!!! Proposisi-proposisi yang nilainya selalu benar disebut proposisi-proposisi yang nilainya selalu salah disebut
- 16. Contoh: Premis 1 : Premis 2 : ’ü£ : Baris pertama dari tabel kebenaran kondisional (implikasi) menunjukkan validitas dari bentuk argumen modus ponen. Premis 1 : Premis 2 : ’ü£ : Jika saya belajar, maka saya lulus ujian (benar) Saya belajar (benar) Saya lulus ujian (benar) Jika x = 7, maka x┬▓ = 49 x = 7 x┬▓ = 49
- 17. ModusTolens Penarikan kesimpulan dengan modus tolens dilakukan dengan simbol matematika: {(p ŌćÆ q) Ōł¦ ~q} ŌćÆ ~p dibaca ŌĆ£implikasi dikonjungsikan terhadap negasi q berimplikasi (menghasilkan) kesimpulan atau konklusi negasi p. Uraian modus tolens dapat ditulis: Premis 1 : Premis 2 : ’ü£ : p ŌćÆ q ~q ~p
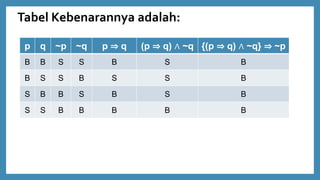
- 18. Tabel Kebenarannya adalah: p q ~p ~q p ŌćÆ q (p ŌćÆ q) Ōł¦ ~q {(p ŌćÆ q) Ōł¦ ~q} ŌćÆ ~p B B S S B S B B S S B S S B S B B S B S B S S B B B B B
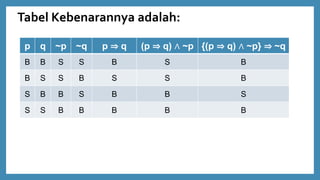
- 19. Tabel Kebenarannya adalah: p q ~p ~q p ŌćÆ q (p ŌćÆ q) Ōł¦ ~p {(p ŌćÆ q) Ōł¦ ~p} ŌćÆ ~q B B S S B S B B S S B S S B S B B S B B S S S B B B B B
- 20. Contoh: Premis 1 : Premis 2 : ’ü£ : Perhatikan bahwa jika p terjadi maka q terjadi, sehingga jika q tidak terjadi maka p tidak terjadi. Premis 1 : Premis 2 : ’ü£ : Jika hari hujan maka saya memakai jas hujan (benar) Saya tidak memakai jas hujan (benar) Hari tidak hujan (benar) Jika ada gula maka ada semut Tidak ada semut Tidak ada gula
- 21. Silogisme Penarikan kesimpulan dengan silogisme dilakukan berdasarkan implikasi-implikasi berturut-turut. Secara simbolik logika penarikan kesimpulan dengan silogisme dituliskan dengan lambang: {(p ŌćÆ q) Ōł¦ (q ŌćÆ r)} ŌćÆ (p ŌćÆ r) Uraian silogisme dapat ditulis: Premis 1 : Premis 2 : ’ü£ : p ŌćÆ q q ŌćÆ r p ŌćÆ r
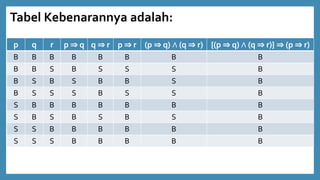
- 22. Tabel Kebenarannya adalah: p q r p ŌćÆ q q ŌćÆ r p ŌćÆ r (p ŌćÆ q) Ōł¦ (q ŌćÆ r) {(p ŌćÆ q) Ōł¦ (q ŌćÆ r)} ŌćÆ (p ŌćÆ r) B B B B B B B B B B S B S S S B B S B S B B S B B S S S B S S B S B B B B B B B S B S B S B S B S S B B B B B B S S S B B B B B
- 23. Contoh: Premis 1 : Premis 2 : ’ü£ : Premis 1 : Premis 2 : ’ü£ : Jika kamu benar maka saya bersalah (benar) Jika saya bersalah maka saya minta maaf (benar) Jika kamu benar maka saya minta maaf (benar) Jika hari ini hujan maka jalanan basah (benar) Jika jalanan basah maka saya tidak berangkat kuliah(benar) Jika hari ini hujan maka saya tidak berangkat kuliah (benar)
- 24. Silogisme Disjungtif Jika ada kemungkinan bahwa kedua pernyataan p dan q dapat sekaligus bernilai benar, maka argumen di bawah ini tidak valid. Premis 1 : Premis 2 : ’ü£ : Tetapi jika ada kemungkinan kedua pernyataan p dan q tidak sekaligus bernilai benar (disjungsi eksklusif), maka silogisme disjungtif di atas adalah valid. p Ōł© q ~p q p Ōł© q q ~p Premis 1 : Premis 2 : ’ü£ : Premis 1 : Premis 2 : ’ü£ : Atau p Ōł© q ~q p
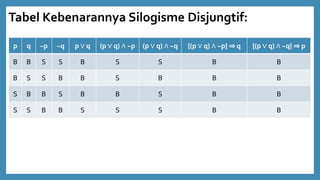
- 25. Tabel Kebenarannya Silogisme Disjungtif: p q ~p ~q p Ōł© q (p Ōł© q) Ōł¦ ~p (p Ōł© q) Ōł¦ ~q {(p Ōł© q) Ōł¦ ~p} ŌćÆ q {(p Ōł© q) Ōł¦ ~q} ŌćÆ p B B S S B S S B B B S S B B S B B B S B B S B B S B B S S B B S S S B B
- 26. Contoh: 1. Premis 1 : Premis 2 : ’ü£ : 2. Premis 1 : Premis 2 : ’ü£ : 3. Premis 1 : Premis 2 : ’ü£ : Pengalaman ini berbahaya atau membosankan (B) Pengalaman ini tidak berbahaya (B) Pengalaman ini membosankan (B) Air ini panas atau dingin (B) Air ini panas (B) Air ini tidak dingin (B) Obyeknya berwarna merah atau sepatu Obyek ini berwarna merah Obyeknya bukan sepatu (tidak valid)
- 27. Konjungsi Premis 1 : Premis 2 : ’ü£ : Artinya: p benar, q benar. Maka p Ōł¦ q benar. Tambahan (Addition) Premis 1 : ’ü£ : Artinya: p benar, maka p Ōł© q benar (tidak peduli nilai benar atau nilai salah yang dimiliki q). p q p Ōł¦ q p Ōł© q p
- 28. Duabentuk argumenvalid yang lainadalah dilema konstruktif dandilema destruktif
- 29. Dilema Konstruktif Premis 1 : Premis 2 : ’ü£ : Dilema konstruktif ini merupakan kombinasi dua argumen modus ponen (periksa argumen modus ponen). Contoh: Premis 1 : Premis 2: ’ü£ : Jika hari hujan, aku akan tinggal di rumah; tetapi jika pacar datang, aku pergi berbelanja Hari ini hujan atau pacar datang Aku akan tinggal di rumah atau pergi berbelanja (p ŌćÆ q) Ōł¦ (r ŌćÆ s) p Ōł© r q Ōł© s
- 30. Dilema Destruktif Premis 1 : Premis 2 : ’ü£ : Dilema destruktif ini merupakan kombinasi dari dua argumen modus tolens (perhatikan argumen modus tolens). Contoh: Premis 1 : Premis 2: ’ü£ : Jika aku memberikan pengakuan, aku akan digantung; dan jika aku tutup mulut, aku akan ditembak mati Aku tidak akan digantung atau ditembak mati Aku tidak akan memberikan pengakuan, atau tidak akan tutup mulut (p ŌćÆ q) Ōł¦ (r ŌćÆ s) ~q Ōł© ~s ~p Ōł© ~r
- 31. Contoh lain penarikan kesimpulan logika
- 32. Contoh: 1. Premis 1 : Premis 2 : ’ü£ : 2. Premis 1 : Premis 2 : ’ü£ : 3. Premis 1 : Premis 2 : ’ü£ : Jika semua pejabat tidak korupsi maka rakyat hidup sejahtera Rakyat hidup sengsara Semua pejabat korupsi (ModusTolens) Tidak ada politikus yang suka berbohong Orang yang tidak suka berbohong adalah orang bijak Semua politikus adalah orang bijak (Silogisme) Setiap rumah memiliki lampu Setiap rumah memiliki televisi Setiap rumah memiliki lampu dan televisi (konjungsi)
- 33. Contoh: 4. Premis 1 : Premis 2 : ’ü£ : 5. Premis 1 : Premis 2 : ’ü£ : 6. Premis 1 : Premis 2 : ’ü£ : Berbelanja tanpa perencanaan mengakibatkan pemborosan Resti selalu berbelanja tanpa perencanaan Resti selalu melakukan pemborosan (Modus Ponen) Jika Ayah di kantor dan Andri di sekolah, maka Ibu di rumah Ibu tidak dirumah Ayah tidak di kantor atau Andri tidak di sekolah (ModusTolens) Jika Fadli Kuliah atau menikah makaAyah menghadiahkannya uang Ayah tidak menghadiahkannya uang Fadli tidak kuliah dan tidak menikah (ModusTolens)
- 34. Contoh: 7. Premis 1 : Premis 2 : ’ü£ : 8. Premis 1 : Premis 2 : ’ü£ : 9. Premis 1 : Premis 2 : ’ü£ : Jika saya ganteng maka pacar saya banyak Jika pacar saya banyak maka saya adalah playboy Jika saya ganteng maka saya adalah playboy (Silogisme) Jika pacar saya cantik maka saya mencintainya Jika saya mencintai pacar saya maka saya menikahinya Jika pacar saya cantik maka saya menikahinya (Silogisme) Jika istri saya cantik atau menawan maka anak saya ganteng Anak saya tidak ganteng Istri saya tidak cantik dan tidak menawan (ModusTolens)








![Negasi Suatu Pernyatan yang Mengandung Kuantor
Negasi dari:
Semua manusia tidak kekal =
Atau:
Semua manusia tidak kekal =
Jika p(x) adalah manusia tidak kekal atau x tidak kekal, maka
ŌĆ£Semua manusia adalah tidak kekalŌĆØ atau ’Ćóx, p(x) bernilai benar,
dan ŌĆ£Beberapa manusia kekalŌĆØ atau ’Ćżx, ~p(x) bernilai salah.
Pernyataan di atas dapat dituliskan dengan simbol:
~ [’Ćóx p(x)] ’é║ ’Ćżx ~p(x)
Tidak benar bahwa semua manusia
tidak kekal
Beberapa manusia kekal](https://image.slidesharecdn.com/kuantor-181122121826/85/Kuantor-dan-Validitas-Pembuktian-8-320.jpg)
![Jadi negasi dari suatu pernyataan yang mengandung kuantor
universal adalah ekivalen dengan pernyataan yang mengandung
kuantor eksistensial (fungsi pernyataan yang dinegasikan) dan
sebaliknya :
~[’Ćżx p(x)] ’é║ ’Ćóx ~p(x)
Contoh:
p :
~p :
q :
~q :
r :
~r :
~r :
Semua mahasiswa rajin belajar
Ada mahasiswa yang tidak rajin belajar
Ada mahasiswa yang rumahnya di Lahewa
Semua mahasiswa rumahnya bukan di Lahewa
Jika semua mahasiswa rajin belajar maka
lulus ujianSemua mahasiswa rajin belajar dan tidak
lulus ujianSemua mahasiswa rajin belajar tetapi tidak lulus
ujian](https://image.slidesharecdn.com/kuantor-181122121826/85/Kuantor-dan-Validitas-Pembuktian-9-320.jpg)