�ݺ�ߣ

Pendahuluan






Komputer digital -> sistem yang memproses informasi
diskrit
Elemen diskrit -> biner (0/1)
Input yang bukan bilangan biner diubah terlebih dahulu
ke dalam bilangan biner.
Sistem bilangan : base atau radix (r)
Macam sistem bilangan :






Desimal : r=10
Biner : r=2
Oktal : r=8
Heksadesimal r=16
dsb

2

Sistem-Sistem Bilangan
 Sistem-Sistem

Bilangan secara matematis:

Bilangan : Dr = d n −1d n − 2  d1d 0 , d −1  d − n
Nilai :

Dr = ∑i = − n d i × r i
n −1

 Contoh-2:
 desimal:

5185.6810 = 5x103 + 1x102 + 8x101 + 5x100 + 6 x 10-1 + 8 x 10-2
= 5x1000 + 1x100 + 8x10 + 5 x 1 + 6x.1 + 8x.01
 biner

(radiks=2, digit={0, 1})

100112 = 1 × 16 + 0 × 8 + 0 × 4 + 1 × 2 + 1 × 1 = 1910
|

|
MSB

LSB

3

101.0012 = 1x4 + 0x2 + 1x1 + 0x.5 + 0x.25 + 1x.125 = 5.12510

Sistem-Sistem Bilangan Umum
Sistem

Radiks

Desimal

r=10

{0,1,2,3,4,5,6,7,8,9}

Biner

r=2

{0,1}

Oktal

r= 8

{0,1,2,3,4,5,6,7}

Heksadesimal

r=16

{0,1,2,3,4,5,6,7,8,9,A, B, C, D, E, F}

2

4

Desimal

0

1

Heksa 0 1
Biner 0000 0001
Oktal

0

1

3
2

3

Himpunan/elemen Digit

5
4

25510
111111112

6
5

Contoh

7
6

8
7

3778

9
8

FF16

10 11 12 13 14 15
9

A

B

C

D

E

F

0010 0011 0100 0101 0110 0111 1000 1001 1010 1011 1100 1101 1110 1111

2

3

4

5

6

7

10 11 12 13 14 15 16 17

4

Radiks-r ke desimal
 Ekspansikan

dgn menggunakan definisi berikut

Dr = ∑ i = − n d i × r
n −1

 Contoh-2:

 1101.1012 =

i

1×23 + 1×22 + 1×20 + 1×2-1 + 1×2-3
= 8 + 4 + 1 + 0.5 + 0.125 = 13.62510

 572.68 =
8

5×82 + 7×81 + 2×80 + 6×8-1
= 320 + 56 + 16 + 0.75 = 392.7510
6

Radiks-r ke desimal (lanj.)
 2A.816 =

2×161 + 10×160 + 8×16-1

16

= 32 + 10 + 0.5 = 42.510
 132.34 =

1×42 + 3×41 + 2×40 + 3×4-1
= 16 + 12 + 2 + 0.75 = 30.7510

 341.245 =
5

3×52 + 4×51 + 1×50 + 2×5-1 + 4×5-2

= 75 + 20 + 1 + 0.4 + 0.16 = 96.5610

7

Desimal ke biner
 Untuk

bilangan desimal bulat

 Gunakan

pembagian dgn 2 secara suksesif sampai
sisanya = 0.
 Sisa-sisa pembagian membentuk jawaban, yaitu
sisa yang pertama akan menjadi least significant bit
(LSB) dan sisa yang terakhir menjadi most
significant bit (MSB).

8

Desimal ke biner (lanj.)
 Contoh:

Konversi 17910 ke biner:

179 / 2 = 89 sisa 1 (LSB)
/ 2 = 44 sisa 1
/ 2 = 22 sisa 0
/ 2 = 11 sisa 0
/ 2 = 5 sisa 1
/ 2 = 2 sisa 1
/ 2 = 1 sisa 0
/ 2 = 0 sisa 1
(MSB)
⇒ 17910 = 101100112
9

 Untuk

bilangan desimal di belakang koma

 kalikan

dengan 2 secara berulang sampai fraksi hasil
perkalian = 0 (atau sampai jumlah penempatan biner
yang diharapkan).

 Digit

kesleuruhan hasil perkalian memrupakan
jawaban, dengan yang pertama  MSB, dan yang
terakhir LSB.

10



Contoh: Konversi 0.312510 ke biner
Digit hasil
.3125 × 2

=

0.625

0

.625 × 2

=

1.25

1

.25 × 2

=

0.50

0

.5 × 2

=

1.0

1

(MSB)

(LSB)

⇒ 0.312510 = .01012

11

Desimal ke Oktal


Untuk bilangan bulat
 Gunakan pembagian dgn 8 secara suksesif sampai
sisanya = 0.
 Sisa-sisa pembagian membentuk jawaban, yaitu sisa
yang pertama akan menjadi LSB dan sisa yang
terakhir menjadi MSB.



Untuk bilangan desimal di belakang koma :
 kalikan dengan 8 secara berulang sampai fraksi hasil
perkalian = 0 (atau sampai jumlah penempatan biner
yang diharapkan).
 Digit keseluruhan hasil perkalian merupakan jawaban,
dengan yang pertama  MSB, dan yang terakhir
LSB.
12

Desimal ke Oktal (lanj.)
Contoh : Konversi 153.513 ke oktal sampai 8 angka di belakang
koma
 Untuk bilangan desimal bulat 153
153 / 8 = 19 sisa 1 (LSB)
/ 8 = 2 sisa 3
/ 8 = 0 sisa 2 (MSB)
⇒ 15310 = 2318


Untuk bilangan desimal dibelakang koma 0.513
0.513 x 8 = 4.104
0.104 x 8 = 0.832
0.832 x 8 = 6.656
0.656 x 8 = 5.248
0.248 x 8 = 1.984
0.984 x 8 = 7.872

4
0
6
5
1
7

(MSB)

(LSB)

⇒ 0.51310 = .4065178

Sehingga 153.51310 = 231.4065178

13

Biner ke Oktal/Heksadesimal
 Base/radix

oktal = 8 = 23
 Base/radix heksadesimal =16 = 2 4
 Konversi dari biner ke oktal maupun ke
heksadesimal dilakukan dengan cara
mengelompokkan bilangan biner tiap 3
digit (oktal) atau 4 digit (heksadesimal)
dimulai dari tanda koma ke kiri dan ke
kanan.
14

Biner ke Oktal/Heksadesimal
 Contoh
 (10

:

110 001 101 011 . 111 100 000 110) 2 =

(2 6
(

1

5

3

.

7

4

0

6 )8

10 1100 0110 1011 . 1111 0000 0110) 2 =

( 2

C

6

B

.

F

0

6 )16

15

Oktal/Heksadesimal ke Biner
 Setiap

digit oktal dikonversi ke 3 digit biner
yang ekivalen.
 Setiap digit heksadesimal dikonversi ke 4
digit biner yang ekivalen.
 Contoh :
 (673.124)8
 (306.D)16

= ( 110 111 011 . 001 010 100 )2

= ( 0011 0000 0110 . 1101 )2
16

1.2 Operasi Matematika
Biner
Penjumlahan
Pengurangan
Perkalian
Pembagian
17

Penjumlahan aritmatika Biner
 Mirip

spt penjumlahan bil. Desimal, dua
bil. biner dijumlahkan melalui
penambahan setiap pasangan bit-bit
bersamaan dengan propagasi carry.

 Contoh:

Cout dr bit ke-5
= Cin dr bit ke-6

18

Pengurangan aritmatika Biner
 Dua

bil. Biner dikurangkan melalui
pengurangan setiap pasangan bit-bit berikut
suatu borrowing, jika diperlukan.
 Contoh:

19

Perkalian Biner
 Contoh:

11
X 13
-------33
11
______
143

11 x 13 = ?
1011
multiplicand (4 bits)
X 1101
multiplier (4 bits)
------------------1011
0000
1011
1011
--------------------10001111
Hasil kali (8 bits)
20

Pembagian Biner
 Contoh

: 15 : 3 = ?

15 = 1111
3 = 11

11
11 1111
11
0011
11 00

21

Pembagian Biner
 Contoh

: 33 : 11 = ?

33 = 100001
11 = 1011

1011

011
100001
0000
10000
1011 1011
1011 0000
22

Latihan konversi bilangan
1. Konversi desimal ke biner, oktal, heksa
a. 1231
b. 673.23
2. Konversi biner ke desimal, oktal, heksa
a. 101110
b. 1110101.11
3. Konversi oktal ke biner
a. 623
b. 715
4. Konversi heksa ke biner
a. 15F
b. A7
23

Latihan op. aritmatika biner
Lakukan operasi aritmatika biner :
 80 : 20 = ?
 13 x 7 = ?
 46 + 27 = ?
 89 – 24 = ?

24

 Komplemen

digunakan untuk menyederhanakan
operasi pengurangan atau untuk manipulasi
logika.
 Ada 2 macam :
 r’s

komplemen
 (r-1)’s komplemen
 Contoh

:

 r=10

(desimal) : 10’s dan 9’s komplemen
 r=2 (biner) : 2’s dan 1’s komplemen
 dst
26

r’s komplemen
⇒ r’s = ( rn – N)
⇒









N : bilangan
r : basis bil.
n : jumlah digit N

10’s komplemen dari 546700
= 1000000 – 546700 = 453300
= 1000000 – 012398 = 987602
= 10000000 – 1011000 = 0101000
= 10000000 – 0101101 = 1010011

27

(r-1)’s komplemen
⇒ (r-1)’s = rn - rm – N
⇒ N : bilangan r : basis bil. n : jumlah digit integer N
m : jumlah digit pecahan N








= 106 - 100 – 546700 = 453299
9’s komplemen dari 0.3267
= 100 - 104 – 0.3267 = 0.6732
= 27 – 20 – 1011000 = 0100111
= 27 - 20 – 0101101 = 1010010

28

Rumusan :
r’s complement = (r-1)’s complement +1
(r-1)’s complement = r’s complement - 1

29

1.4 Operasi Aritmatika
Menggunakan Komplemen

30

Pengurangan dengan
2’s Komplemen
 Pengurangan

2 n-digit bilangan M-N pada basis
r dapat dilakukan sbb :
 Tambahkan

M dengan r’s komplemen dari N
M + ( rn – N ) = M - N + r n
 Jika M>=N, hasil penjumlahan menghasilkan carry
(sisa), yang kemudian dibuang dengan cara
mengurangi dengan rn.
hasil akhir = M - N
 Jika M<N, hasil penjumlahan tidak menghasilkan
carry
hasil = rn – ( N – M )
hasil akhir diperoleh dari r’s komplemen dari hasil
hasil akhir = - r’s komplemen (hasil)
31

Contoh (1)
Menggunakan 10’s komplemen, lakukan
pengurangan 72532 – 3250.
M=
10’s komplemen N =
Jumlah =
Buang carry 105 =
Hasil =

72532
96750 +
169282
100000 –
69282
32

Contoh (2)
pengurangan 3250 - 72532.
M=
10’s komplemen N =
Jumlah =

03250
27468 +
30718

Hasil = -(10’s komplemen 30718) = -69282
33

Contoh (3)
pengurangan 1010100 – 1000011
M=
1010100
2’s komplemen N =
0111101 +
Jumlah = 10010001
Buang carry 27 = 10000000 0010001
34

Contoh (4)
pengurangan 1000011 – 1010100
M
2’s komplemen N
Jumlah

= 1000011
= 0101100 +
= 1101111

Hasil = - (2’s komplemen 1101111) = -0010001
35

Pengurangan dengan
1’s Komplemen
 Pengurangan

2 n-digit bilangan M-N pada basis
r dapat dilakukan sbb :
 Tambahkan

M dengan r’s komplemen dari N
M + ( r n – r m – N ) = M - N + r n - rm
 Jika M>=N, hasil penjumlahan menghasilkan carry
(sisa), yang kemudian dibuang dengan cara
menambahkan carry ke hasil penjumlahan
 Jika M<N, hasil penjumlahan tidak menghasilkan
carry. Hasil akhir diperoleh dari (r-1)’s komplemen
dari hasil.
hasil akhir = - (r-1)’s komplemen (hasil)
36

Contoh (1)
X – Y = 1010100 – 1000011
X
1’s komplemen N
Jumlah
Tambahkan carry

=
1010100
=
0111100 +
= 10010000
=
1 +
0010001
37

Contoh (2)
X – Y = 1000011 – 1010100
M
1’s komplemen N
Jumlah

= 1000011
= 0101011 +
= 1101110

Hasil = - (1’s komplemen 1101110) = -0010001
38

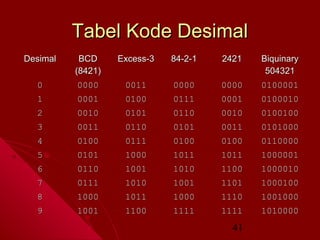
Kode Desimal
 Kode

biner untuk bilangan desimal
minimum terdiri dari 4 digit.
 Ada 5 macam kode desimal :
 BCD

(Binary Code Decimal) atau 8421
 Excess-3, diperoleh dari BCD + (11) 2
 84-2-1
 2421
 Biquinary

atau 5043210
40

Tabel Kode Desimal
Desimal

BCD
(8421)

Excess-3

84-2-1

2421

Biquinary
504321

0

0000

0011

0000

0000

0100001

1

0001

0100

0111

0001

0100010

2

0010

0101

0110

0010

0100100

3

0011

0110

0101

0011

0101000

4

0100

0111

0100

0100

0110000

5

0101

1000

1011

1011

1000001

6

0110

1001

1010

1100

1000010

7

0111

1010

1001

1101

1000100

8

1000

1011

1000

1110

1001000

9

1001

1100

1111

1111

1010000

41

Konversi Desimal ke Kode Biner
 Setiap

digit bilangan desimal di konversi
ke n-digit kode desimal.
 Contoh : Bilangan desimal 639
 BCD
 Excess-3
 84-2-1
 2421
 Biquinary

: 0110 0011 1001
: 1001 0110 1100
: 1010 0101 1111
: 1100 0011 1111
: 1000010 0101000 1010000
42

Komplemen
 9’s

komplemen dari suatu bilangan desimal
diperoleh mengubah 1 jadi 0 dan 0 jadi 1,
kecuali BCD.
 Contoh :
 395

dengan 2421 = 0011 1111 1011
9’s komplemen dari 395 = 1100 0000 0100 =
604
 123 dengan BCD = 0001 0010 0011
9’s komplemen dari 123 = 1110 1101 1100 = xxx
43

Kode Pendeteksian Error
 Pengiriman

data melalui media kabel
ataupun yang lain kadang menimbulkan
error.
 Error terjadi ketika data yang diterima
tidak sesuai dengan data yang dikirim
atau perubahan 0 jadi 1 atau sebaliknya.
 Pendeteksian error dapat dilakukan
dengan menambahkan satu bit (parity bit)
pada akhir data.
44

Parity Bit
 Merupakan

ekstra bit yang disisipkan
pada pesan untuk menjadikan total 1’s
yang dikirim genap atau ganjil.
 Macam
 Odd

Parity (parity ganjil)
 Even Parity (parity genap)

45

Odd Parity

Even Parity

Message

P

Message

P

0000

1

0000

0

0001

0

0001

1

0010

0

0010

1

0011

1

0011

0

0100

0

0100

1

0101

1

0101

0

0110

1

0110

0

0111

0

0111

1

1000

0

1000

1

1001

1

1001

0

1010

1

1010

0

1011

0

1011

1

1100

1

1100

0

1101

0

1101

1

1110

0

1110

1

1111

1

1111

46

0

 Keunggulan

gray
code daripada
bilangan biner bahwa
hanya satu bit yang
berubah untuk ke
bilangan selanjutnya

Gray Code

0

0000

1

Gray Code

Desimal

0001

2

0011

3

0010

4

0110

5

0111

6

0101

7

0100

8

1100

9

1101

10

1111

11

1110

12

1010

13

1011

14

1001

15

47

1000

Kode ASCII
 ASCII

(American Standard Code fir
Information Interchange)
 Terdiri dari 128 karakter, yaitu :
 26

huruf besar (A sampai Z)
 26 huruf kecil (a sampai z)
 10 numerik (1 sampai 9)
 32 karakter spesial , spt %, * dan $
 34 karakter nonprinting
48

b7b6b5

b4b3b2b1

000

001

010

011

100

101

110

111

0000

NUL

DLE

SP

0

@

P

`

p

0001

SOH

DC1

!

1

A

Q

a

q

0010

STX

DC2

“

2

B

R

b

r

0011

ETX

DC3

#

3

C

S

c

s

0100

EOT

DC4

$

4

D

T

d

t

0101

ENQ

NAK

%

5

E

U

e

u

0110

ACK

SYN

&

6

F

V

f

v

0111

BEL

ETB

‘

7

G

W

g

w

1000

BS

CAN

(

8

H

X

h

x

1001

HT

EM

)

9

I

Y

i

y

1010

LF

SUB

*

:

J

Z

j

z

1011

VT

ESC

+

;

K

[

k

{

1100

FF

FS

,

<

L

l

|

1101

CR

GS

-

=

M

m

}

]49

Contoh
 Huruf

‘A’ memiliki kode ASCII 1000001
(kolom 100, baris 0001)
 Karakter ‘{‘ memiliki kode ASCII 1111011
 Dsb.

50

Latihan
1. Lakukan proses pengurangan dengan
dan tanpa komplemen (ubah dulu ke
biner) :
482 – 256 = ?
2. Lakukan pengurangan 2 bilangan
dengan menggunakan komplemen
(ubah dulu ke biner)
324 – 742 = ?
51

�ݺ�ߣ

Kuliah 1 sistem_bilangan

More Related Content

Kuliah 1 sistem_bilangan