特徴选択のための尝补蝉蝉辞解列挙
- 1. 特徴选択のための尝补蝉蝉辞解列挙(AAAI’17) 原 聡1,2、前原 貴憲3 1 ERATO感謝祭 Season IV 1) 国立情報学研究所 2) JST, ERATO, 河原林巨大グラフプロジェクト 3) 理研AIP
- 2. 研究背景 2
- 3. 研究背景:特徴選択は完璧か? n 『特徴選択を使うと、タスクに関連する特徴量と、タスクに関連し ない特徴量とを識別することができる』と言われている。 ? Lassoを使うとモデルのスパースな表現が得られる。 ? Lassoによって選ばれた特徴量が重要な特徴量だと言われている。 3
- 4. 研究背景:特徴選択は完璧か? n 『特徴選択を使うと、タスクに関連する特徴量と、タスクに関連し ない特徴量とを識別することができる』と言われている。 ? Lassoを使うとモデルのスパースな表現が得られる。 ? Lassoによって選ばれた特徴量が重要な特徴量だと言われている。 n しかし、機械学習に完璧はありえない。 ? 有限のデータから学習する以上、ある程度のエラーは起こりうる。 ? データ由来?学習手法由来のバイアスがのることがある。 4
- 5. 研究背景:特徴選択は完璧か? n 『特徴選択を使うと、タスクに関連する特徴量と、タスクに関連し ない特徴量とを識別することができる』と言われている。 ? Lassoを使うとモデルのスパースな表現が得られる。 ? Lassoによって選ばれた特徴量が重要な特徴量だと言われている。 n しかし、機械学習に完璧はありえない。 ? 有限のデータから学習する以上、ある程度のエラーは起こりうる。 ? データ由来?学習手法由来のバイアスがのることがある。 5 機械学習は時として間違える。 機械学習がミスすると。。。
- 11. 研究背景:ユーザに信頼される特徴選択をしたい。 n しかし、“間違えない特徴選択”は難しい。 ? Lassoは選ばれた特徴量が“真に重要な特徴量”であることが保証されな い。 - Adaptive Lassoをはじめ、様々な改善法が考案されている。 - しかし、有限のデータから学習している以上、エラーは避けられない。 11
- 12. 研究背景:ユーザに信頼される特徴選択をしたい。 n しかし、“間違えない特徴選択”は難しい。 ? Lassoは選ばれた特徴量が“真に重要な特徴量”であることが保証されな い。 - Adaptive Lassoをはじめ、様々な改善法が考案されている。 - しかし、有限のデータから学習している以上、エラーは避けられない。 n 本研究のアイディア ? そもそも“重要な特徴量の組”を一つ探そうとしているから難しい。 12
- 13. 研究背景:ユーザに信頼される特徴選択をしたい。 n しかし、“間違えない特徴選択”は難しい。 ? Lassoは選ばれた特徴量が“真に重要な特徴量”であることが保証されな い。 - Adaptive Lassoをはじめ、様々な改善法が考案されている。 - しかし、有限のデータから学習している以上、エラーは避けられない。 n 本研究のアイディア ? そもそも“重要な特徴量の組”を一つ探そうとしているから難しい。 ? “重要な特徴量の組”をたくさん見つけて、それをユーザに提示したらどう か? → 「Lasso解を複数列挙する問題」を考える。 13
- 14. 研究背景:ユーザに信頼される特徴選択をしたい。 n しかし、“間違えない特徴選択”は難しい。 ? Lassoは選ばれた特徴量が“真に重要な特徴量”であることが保証されな い。 - Adaptive Lassoをはじめ、様々な改善法が考案されている。 - しかし、有限のデータから学習している以上、エラーは避けられない。 n 本研究のアイディア ? そもそも“重要な特徴量の組”を一つ探そうとしているから難しい。 ? “重要な特徴量の組”をたくさん見つけて、それをユーザに提示したらどう か? → 「Lasso解を複数列挙する問題」を考える。 14 Xという病気に関連す る項目は。。。
- 15. 研究背景:ユーザに信頼される特徴選択をしたい。 n しかし、“間違えない特徴選択”は難しい。 ? Lassoは選ばれた特徴量が“真に重要な特徴量”であることが保証されな い。 - Adaptive Lassoをはじめ、様々な改善法が考案されている。 - しかし、有限のデータから学習している以上、エラーは避けられない。 n 本研究のアイディア ? そもそも“重要な特徴量の組”を一つ探そうとしているから難しい。 ? “重要な特徴量の組”をたくさん見つけて、それをユーザに提示したらどう か? → 「Lasso解を複数列挙する問題」を考える。 15 Xという病気に関連す る項目は。。。 「身長」と「血圧」 う?ん?
- 16. 研究背景:ユーザに信頼される特徴選択をしたい。 n しかし、“間違えない特徴選択”は難しい。 ? Lassoは選ばれた特徴量が“真に重要な特徴量”であることが保証されな い。 - Adaptive Lassoをはじめ、様々な改善法が考案されている。 - しかし、有限のデータから学習している以上、エラーは避けられない。 n 本研究のアイディア ? そもそも“重要な特徴量の組”を一つ探そうとしているから難しい。 ? “重要な特徴量の組”をたくさん見つけて、それをユーザに提示したらどう か? → 「Lasso解を複数列挙する問題」を考える。 16 Xという病気に関連す る項目は。。。 「身長」と「血圧」 う?ん? 「体重」と「血糖値」 う?ん?
- 17. 研究背景:ユーザに信頼される特徴選択をしたい。 n しかし、“間違えない特徴選択”は難しい。 ? Lassoは選ばれた特徴量が“真に重要な特徴量”であることが保証されな い。 - Adaptive Lassoをはじめ、様々な改善法が考案されている。 - しかし、有限のデータから学習している以上、エラーは避けられない。 n 本研究のアイディア ? そもそも“重要な特徴量の組”を一つ探そうとしているから難しい。 ? “重要な特徴量の組”をたくさん見つけて、それをユーザに提示したらどう か? → 「Lasso解を複数列挙する問題」を考える。 17 Xという病気に関連す る項目は。。。 「身長」と「血圧」 う?ん? 「体重」と「血糖値」 う?ん? 「体重」と「血圧」 これだ!!
- 18. Lasso 18
- 19. Lassoによる特徴選択 スパース線形回帰問題 Given: 入出力のペア ?", ?" ∈ ?'×? ? = 1, 2, … , ? Find: 回帰係数? ∈ ?' s.t. ?" 1 ? ≈ ? (? = 1, 2, … , ?) ただし、?は非ゼロ要素が少ない(スパース) n スパース性 ? 物理的要請 - 大量の特徴量のうち、効く特徴量は少ないはずという直感。 ? 解釈性向上 - 解から意味のある特徴量を見出したい。変数の絞込み。 解法:Lasso回帰( ?6正則化) ?? = argmin > 1 2 ?? ? ? A + ? ? 6 ? Lasso解??はスパース。supp(??) = {? ∶ ?" ? ≠ 0}が重要な特徴量。 19
- 20. Lassoの理論的正当性:復元定理 Lasso解:?? = argmin > 6 A ?? ? ? A + ? ? 6 適当な設定の元で、Lasso解??は真のパラメータ?Lのサポート(非 零要素)を高い確率で復元する。 n 仮定 ? 真のモデルが? = ??L + ?; ?Lはスパース, ? ~ ?(0, ?A) ? 正則化パラメータ?は十分小さい。 ? ?の各行は十分独立(高相関な特徴量はない)。 n 上記仮定の元で、高い確率で真のパラメータ?Lのサポートが復 元できる。 supp(??) = supp(?L) 20
- 21. Lassoの限界:重要な特徴量を見落とす。 n 高次元データでは、類似した特徴量が存在することが多い。 ? 類似特徴量のうち、どれを使っても同等の予測精度のモデルが作れる。 ? 「?の各行は十分独立(高相関な特徴量はない)」という仮定が成立しない 場合に相当。 →このような場合、Lassoは類似特徴量の一部だけを使い残りを無 視する。 n Lassoの限界:類似特徴量の中の重要な特徴量を見落とす。 ? 例えば、「身長」と「体重」のような相関の高い特徴量のうち、片方(例えば 「身長」)だけを使ったモデルを出力する。 →「体重」を見落とす。「体重」を使ったモデルを期待するユーザとの間に齟 齬が起きる。 n 本研究:「身長」、「体重」それぞれを使ったモデルを両方出力す る。 21
- 23. 問題の定式化と提案法 23
- 24. 問題の定式化:Lasso解の列挙 n 解のサポートを? ? {?6, ?A, … , ?'}に制限したLasso: Lasso ? = min > 6 A ?? ? ? A + ? ? 6 s.t. supp ? ? ? 問題:Lasso解の列挙 Lasso ? の小さい順に極小の?を?個列挙する。 (極小:supp ? = ?となるもの。それ以外は冗長。) 【注意】正則化パスに基づいた解の列挙ではない。 ? 正則化パスでは疎な解から密な解へと?を変化させた時の解を列挙する。 ? 本問題では?固定の元で、目的関数値が昇順になるように解のサポートを列 挙する。 ? ?6, ?A, ?V , ?6, ?A, ?W , ?6, ?W, ?X , ?6, ?A , … 24 最適解での目的関数値をLasso ? とする。
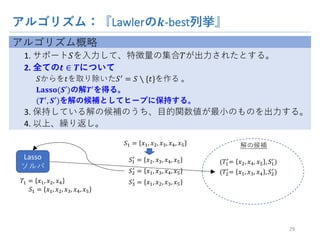
- 25. アルゴリズム:『Lawlerの ?-best列挙』 アルゴリズム概略 1. サポート?を入力して、特徴量の集合?が出力されたとする。 2. 全ての? ∈ ?について ?からを?を取り除いた? = ? ? {?}を作る 。 Lasso(?′)の解?′を得る。 (? , ?′)を解の候補としてヒープに保持する。 3. 保持している解の候補のうち、目的関数値が最小のものを出力する。 4. 以上、繰り返し。 25
- 26. アルゴリズム:『Lawlerの ?-best列挙』 アルゴリズム概略 1. サポート ?を入力して、特徴量の集合 ?が出力されたとする。 2. 全ての? ∈ ?について ?からを?を取り除いた? = ? ? {?}を作る 。 Lasso(?′)の解?′を得る。 (? , ?′)を解の候補としてヒープに保持する。 3. 保持している解の候補のうち、目的関数値が最小のものを出力する。 4. 以上、繰り返し。 26 解の候補 Lasso ソルバ ? = ?6, ?A, ?V 出力 ? = ?6, ?A, ?W, ?V, ?X ?6 = ?6, ?A, ?V ?6 = ?6, ?A, ?W, ?V, ?X
- 27. アルゴリズム:『Lawlerの ?-best列挙』 アルゴリズム概略 1. サポート?を入力して、特徴量の集合?が出力されたとする。 2. 全ての ? ∈ ?について ?からを ?を取り除いた ? = ? ? {?}を作る 。 Lasso(?′)の解?′を得る。 (? , ?′)を解の候補としてヒープに保持する。 3. 保持している解の候補のうち、目的関数値が最小のものを出力する。 4. 以上、繰り返し。 27 解の候補 ?6 = ?A, ?W, ?V, ?X ?A = ?6, ?W, ?V, ?X ?W = ?6, ?A, ?W, ?X ?6 = ?6, ?A, ?W, ?V, ?X Lasso ソルバ ?6 = ?6, ?A, ?V ?6 = ?6, ?A, ?W, ?V, ?X
- 28. アルゴリズム:『Lawlerの ?-best列挙』 アルゴリズム概略 1. サポート?を入力して、特徴量の集合?が出力されたとする。 2. 全ての ? ∈ ?について ?からを?を取り除いた? = ? ? {?}を作る 。 ?????(?′)の解 ?′を得る。 (? , ?′)を解の候補としてヒープに保持する。 3. 保持している解の候補のうち、目的関数値が最小のものを出力する。 4. 以上、繰り返し。 28 解の候補 (?6 = ?A, ?V, ?X , ?6 )?6 = ?A, ?W, ?V, ?X ?A = ?6, ?W, ?V, ?X ?W = ?6, ?A, ?W, ?X ?6 = ?6, ?A, ?W, ?V, ?X Lasso ソルバ ?6 = ?6, ?A, ?V ?6 = ?6, ?A, ?W, ?V, ?X
- 29. アルゴリズム:『Lawlerの ?-best列挙』 アルゴリズム概略 1. サポート?を入力して、特徴量の集合?が出力されたとする。 2. 全ての ? ∈ ?について ?からを?を取り除いた? = ? ? {?}を作る 。 ?????(?′)の解 ?′を得る。 (? , ?′)を解の候補としてヒープに保持する。 3. 保持している解の候補のうち、目的関数値が最小のものを出力する。 4. 以上、繰り返し。 29 解の候補 (?6 = ?A, ?V, ?X , ?6 )?6 = ?A, ?W, ?V, ?X ?A = ?6, ?W, ?V, ?X ?W = ?6, ?A, ?W, ?X ?6 = ?6, ?A, ?W, ?V, ?X Lasso ソルバ (?A = ?6, ?W, ?V , ?A ) ?6 = ?6, ?A, ?V ?6 = ?6, ?A, ?W, ?V, ?X
- 30. アルゴリズム:『Lawlerの ?-best列挙』 アルゴリズム概略 1. サポート?を入力して、特徴量の集合?が出力されたとする。 2. 全ての ? ∈ ?について ?からを?を取り除いた? = ? ? {?}を作る 。 ?????(?′)の解 ?′を得る。 (? , ?′)を解の候補としてヒープに保持する。 3. 保持している解の候補のうち、目的関数値が最小のものを出力する。 4. 以上、繰り返し。 30 解の候補 (?6 = ?A, ?V, ?X , ?6 )?6 = ?A, ?W, ?V, ?X ?A = ?6, ?W, ?V, ?X ?W = ?6, ?A, ?W, ?X ?6 = ?6, ?A, ?W, ?V, ?X Lasso ソルバ (?A = ?6, ?W, ?V , ?A ) (?W = ?6, ?A, ?X , ?W )?6 = ?6, ?A, ?V ?6 = ?6, ?A, ?W, ?V, ?X
- 31. アルゴリズム:『Lawlerの ?-best列挙』 アルゴリズム概略 1. サポート?を入力して、特徴量の集合?が出力されたとする。 2. 全ての? ∈ ?について ?からを?を取り除いた? = ? ? {?}を作る 。 ?????(?′)の解?′を得る。 (? , ?′)を解の候補としてヒープに保持する。 3. 保持している解の候補のうち、目的関数値が最小のものを出力する。 4. 以上、繰り返し。 31 解の候補 (?6 = ?A, ?V, ?X , ?6 ) Lasso ソルバ (?A = ?6, ?W, ?V , ?A ) (?W = ?6, ?A, ?X , ?W )出力 ?A = ?A, ?V, ?X ?A = ?A, ?W, ?V, ?X ?6 = ?6, ?A, ?V ?6 = ?6, ?A, ?W, ?V, ?X
- 32. アルゴリズム:『Lawlerの ?-best列挙』 アルゴリズム概略 1. サポート?を入力して、特徴量の集合?が出力されたとする。 2. 全ての ? ∈ ?について ?からを ?を取り除いた ? = ? ? {?}を作る 。 Lasso(?′)の解?′を得る。 (? , ?′)を解の候補としてヒープに保持する。 3. 保持している解の候補のうち、目的関数値が最小のものを出力する。 4. 以上、繰り返し。 32 解の候補 Lasso ソルバ ?6 = ?6, ?A, ?V ?6 = ?6, ?A, ?W, ?V, ?X (?A = ?6, ?W, ?V , ?A ) (?W = ?6, ?A, ?X , ?W ) ?A = ?A, ?V, ?X ?A = ?A, ?W, ?V, ?X ?V = ?W, ?V, ?X ?X = ?A, ?W, ?X ?j = ?A, ?W, ?V ?A = ?A, ?W, ?V, ?X
- 33. アルゴリズムの妥当性 定理 提案法によりLasso ? の小さい順に極小の?を列挙できる。 n 不要な探索をスキップすることで、提案法を効率化できる。 ? 既に探索した?を重複して探索しないようにする。取り除く変数の履歴を保 持する。 ? 探索したことのない? についても、Lassoの最適性条件から解が既に探索 済みのものと一致することが判定できることがある。 33
- 34. 列挙版の復元定理 定理概略 適当な仮定の元で、十分たくさん列挙すれば、高い確率で列挙した解の中に supp(?L)が含まれる。 n 適当な仮定??い確率: ? 正則化パラメータ?は?分?さい(?Lの?ゼロ成分を下からバウンド)。 ? ノイズが?さいほど確率は?い。 n 列挙個数について?えること: ? 正則化パラメータ?が?さいほど列挙すべき要素が増える。 ? ?の独?性が低い(高相関の特徴量が多い)ほど列挙すべき要素が増え る。 34
- 35. 実験結果 35
- 36. 実験1. シロイズナの開花 n Thaliana gene expression data (Atwell et al. ’10): どの遺伝?が開花に効くかを知りたい。 ? ? ∈ ?A6j6Wk:遺伝?各パターンが?起しているかどうか(2 値) ? ? ∈ ?:発現量 ? データ数(個体数):134 36 50個列挙しても、目的関数値は0.05% しか増加しなかった。 大域解が6個あった。 解のサポートのサイズは 大体40~45くらい。 大域解が複数ある = 単純にLassoを適用すると、6個のうちの1つが見つかるだけ。他の特徴量は見落とす。
- 37. 実験2. ニュース記事の分類 n 20 Newsgroups Data (Lang’95); ibm vs mac ニュース記事を二つのカテゴリに分類するのに特徴的な単語を知りたい。 ? ? ∈ ?66jVl:単語の発現(実数値、tf-idf) ? ? ∈ {ibm, mac} :記事のカテゴリ(2値) ? データ数(投稿数):1168 → 分類問題なので、ロジスティック回帰に提案法を適用。 37 大域解にあった語 列挙解で置き換わった語 drive, os, diskのようなibmマシン(Windows 機)に特有の単語が見落とされていたのが 見つかった。 040, 610のようなmacマシン(型番)に特有 の単語が見落とされていたのが見つかった。
- 38. まとめ n 問題意識:ユーザに信頼される特徴選択をしたい。 ? 単一の特徴選択結果を出力するのでなく、複数の結果を列挙して出力す る。 n 「Lasso解のサポート列挙」として問題を定式化した。 n Lawlerの?-best フレームワークを適?した効率的なアルゴリズ ムを設計。 n 列挙版のスパース復元定理を証明した。 ? どれだけ列挙するかは問題パラメタ依存。 n 実験より,実際の特徴選択問題には「同じくらいの品質の解が ?量に存在する」ことを確認。 ? Lasso で得られた特徴量を安易に信じるのは危険。 38 GitHub: sato9hara/LassoVariants
- 39. 補足資料 39
- 40. 列挙版の復元定理(完全版) n 仮定:? = ??L + ?; ?Lスパース, ? ~ ?(0, ?^2) ? ??L ? ? A ≤ ? ??? ? ? A for some ? ≥ 0 ? ??? ? ? A ≤ ? for some ? ≥ 0 ? ?? ≠ 0 with ?? A ≤ 1 + ? ?, ?vw 6 ≤ ? ?vwy 6 for some ? ≥ max{1, ?A} 定理1:No False Inclusion By enumerating solutions up to ? ? ? ≥ ??(??), we can find ? { , ? { , 1 ≤ ? ≤ ? such that supp ? { ? supp ?L ? ? { and ? ? { ≤ ?(?L). 定理2:No False Exclusion Let ? { , ? { be an enumerated solution where supp ? { ? supp ?L ? ? { . If ?vw 1 ?vw is invertible, then we have supp ? { ? ? ∶ ?" L > 2? ?vw 1 ?vw ~6 ? with probability 1 ? ?L exp ??A/2? ???… ?vw 1 ?vw . 40