LBNLppt
- 1. 30th April 2010 Friday, April 30, 2010
- 2. 30th April 2010 Non-premixed ’¼éame extinction phenomena: analytical and numerical investigations Friday, April 30, 2010
- 3. 30th April 2010 Non-premixed ’¼éame extinction phenomena: analytical and numerical investigations Praveen Narayanan Department of Fire Protection Engineering University of Maryland, College Park, MD-20740 Sponsors: DOE Of’¼üce of Science (INCITE - Innovative and Novel Computational Impact on Theory and Experiment - Program); and National Science Foundation (CBET) Friday, April 30, 2010
- 4. Scholastic background Friday, April 30, 2010
- 5. Scholastic background Ō£ż PhD: Mechanical/Fire Protection Engineering ŌĆó University of Maryland, College Park (2005-present) ŌĆó Thesis topic: Direct Numerical Simulations of non-premixed ’¼éame extinction phenomena ŌĆó Advisers/collaborators: Dr. Arnaud Trouv├® (UMD), Dr. Howard Baum (UMD), Dr. Hong Im (UMich), Paul Arias (UMich) Friday, April 30, 2010
- 6. Scholastic background Ō£ż PhD: Mechanical/Fire Protection Engineering ŌĆó University of Maryland, College Park (2005-present) ŌĆó Thesis topic: Direct Numerical Simulations of non-premixed ’¼éame extinction phenomena ŌĆó Advisers/collaborators: Dr. Arnaud Trouv├® (UMD), Dr. Howard Baum (UMD), Dr. Hong Im (UMich), Paul Arias (UMich) Ō£ż Batchelor and Master of Technology: Chemical Engineering ŌĆó Indian Institute of Technology Madras, Chennai, India (2000-2005) ŌĆó Masters thesis: Implementation of high order compact schemes for incompressible ’¼éows Friday, April 30, 2010
- 7. Research overview Ō£ż ŌĆśFlame extinction` phenomena in non-premixed ’¼éames ŌĆó Background and motivation ŌĆó Phenomenological description ŌĆó Premise, hypothesis ŌĆó Problems investigated ŌĆó Solution approaches and results Ō£ż Future HPC research in ’¼üre/combustion phenomena Friday, April 30, 2010
- 8. Background and motivation Friday, April 30, 2010
- 9. Ō£ż What is a diffusion ’¼éame? ŌĆó Diffusion ’¼éames (or non-premixed ’¼éames): fuel and oxidizer initially unmixed Ō£” Examples: ’¼üres, diesel engines Fuel Flame Air Diffusion ’¼éames Friday, April 30, 2010
- 10. Diffusion ’¼éame extinction Ō£ż Combustion science ŌĆó Impacts performance of non-premixed combustion systems ŌĆó Determines turbulent ’¼éame structure and levels of pollutant emission (NOx, soot, CO) Ō£ż Engine applications: extinction caused by high turbulence intensities in diesel engines (momentum driven, large Reynolds number ’¼éows Diesel engine Friday, April 30, 2010
- 11. Diffusion ’¼éame extinction Ō£ż Fire applications ŌĆó Extinction caused by air vitiation in underventilated compartment ’¼üres ŌĆó Forest ’¼üres, oil spills ŌĆó Sprinkler systems Ō£” Extinction caused by inert gaseous agents or water spray suppression systems pool fire sprinklers Friday, April 30, 2010
- 12. Diffusion ’¼éame extinction smoke Air Fuel Air Extinction Flame surface (Sunderland et al) Ō£ż What is ’¼éame extinction? ŌĆó A ŌĆśhole` in ’¼éame: mixing without chemical reaction ŌĆó Examples: suppressing (or extinguishing) ’¼üres from water spray, blowing out candle Friday, April 30, 2010
- 13. Phenomenology Friday, April 30, 2010
- 14. Diffusion ’¼éame extinction Fuel side Oxidizer side Flame Fuel side Oxidizer side Flame Fuel side Oxidizer side Flame Friday, April 30, 2010
- 15. Diffusion ’¼éame extinction Ō£ż Types of ’¼éame extinction phenomena Fuel side Oxidizer side Flame Fuel side Oxidizer side Flame Fuel side Oxidizer side Flame Friday, April 30, 2010
- 16. Diffusion ’¼éame extinction Ō£ż Types of ’¼éame extinction phenomena ŌĆó Aerodynamic quenching: ’¼éame weakening due to ’¼éow-induced perturbations (insuf’¼ücient residence time-blowing out a candle) Fuel side Oxidizer side Flame Fuel side Oxidizer side Flame Fuel side Oxidizer side Flame Friday, April 30, 2010
- 17. Diffusion ’¼éame extinction Ō£ż Types of ’¼éame extinction phenomena ŌĆó Aerodynamic quenching: ’¼éame weakening due to ’¼éow-induced perturbations (insuf’¼ücient residence time-blowing out a candle) ŌĆó Thermal quenching: ’¼éame weakening due to heat losses (wall cooling, thermal radiation, evaporative cooling in suppression systems) Fuel side Oxidizer side Flame Fuel side Oxidizer side Flame Fuel side Oxidizer side Flame Friday, April 30, 2010
- 18. Diffusion ’¼éame extinction Ō£ż Types of ’¼éame extinction phenomena ŌĆó Aerodynamic quenching: ’¼éame weakening due to ’¼éow-induced perturbations (insuf’¼ücient residence time-blowing out a candle) ŌĆó Thermal quenching: ’¼éame weakening due to heat losses (wall cooling, thermal radiation, evaporative cooling in suppression systems) ŌĆó Quenching by dilution: insuf’¼ücient fuel/oxidizer concentration (air vitiation in under-ventilated ’¼üres) Fuel side Oxidizer side Flame Fuel side Oxidizer side Flame Fuel side Oxidizer side Flame Friday, April 30, 2010
- 19. Types of ’¼éame extinction phenomena Ō£ż Aerodynamic quenching ŌĆó Blowout at large stretch rates (also known as kinetic extinction) ŌĆó Extinction criterion Ō£ż Sources ŌĆó Linan, 1974, ŌĆ£Acta AstronauticaŌĆØ ŌĆó Williams, 1975, ŌĆ£Combustion theoryŌĆØ ŌĆó Carrier, Fendell & Marble, 1975, ŌĆ£SIAM Journal of Applied MathematicsŌĆØ Friday, April 30, 2010
- 20. Types of ’¼éame extinction phenomena Ō£ż Thermal quenching: ŌĆó Radiative extinction (large radiation heat losses) ŌĆó Extinction due to evaporative cooling ŌĆó Extinction criterion ŌĆó Sources Ō£” Sohrab, Li├▒an & Williams (1982) ŌĆ£Combustion Science and TechnologyŌĆØ Ō£” Chao, Law & TŌĆÖien (1992), ŌĆ£Combustion and FlameŌĆØ Ō£” TŌĆÖien (1986), ŌĆ£Combustion and ’¼éameŌĆØ Friday, April 30, 2010
- 21. The premise: ŌĆśuni’¼üedŌĆÖ extinction criterion Friday, April 30, 2010
- 22. Questions Friday, April 30, 2010
- 23. Questions Ō£ż Whether extinction can be described in phenomenological terms with a consistent mathematical model for cases with Friday, April 30, 2010
- 24. Questions Ō£ż Whether extinction can be described in phenomenological terms with a consistent mathematical model for cases with ŌĆó Stretch (due to turbulence) Friday, April 30, 2010
- 25. Questions Ō£ż Whether extinction can be described in phenomenological terms with a consistent mathematical model for cases with ŌĆó Stretch (due to turbulence) ŌĆó Radiative heat losses (soot, CO2, H2O, other gases) Friday, April 30, 2010
- 26. Questions Ō£ż Whether extinction can be described in phenomenological terms with a consistent mathematical model for cases with ŌĆó Stretch (due to turbulence) ŌĆó Radiative heat losses (soot, CO2, H2O, other gases) ŌĆó Evaporative cooling (suppression from water droplets) Friday, April 30, 2010
- 27. Questions Ō£ż Whether extinction can be described in phenomenological terms with a consistent mathematical model for cases with ŌĆó Stretch (due to turbulence) ŌĆó Radiative heat losses (soot, CO2, H2O, other gases) ŌĆó Evaporative cooling (suppression from water droplets) ŌĆó A combination of the above Friday, April 30, 2010
- 28. Questions Ō£ż Whether extinction can be described in phenomenological terms with a consistent mathematical model for cases with ŌĆó Stretch (due to turbulence) ŌĆó Radiative heat losses (soot, CO2, H2O, other gases) ŌĆó Evaporative cooling (suppression from water droplets) ŌĆó A combination of the above Ō£ż What kind of diagnostics may be developed to qualify (or quantify) extinction? Friday, April 30, 2010
- 29. The extinction ŌĆścriterionŌĆÖ Ō£ż The Damk├Čhler number Ō£ż Code supplies both quantities Ō£ż Need to test if hypothesis holds Friday, April 30, 2010
- 30. The extinction ŌĆścriterionŌĆÖ Ō£ż The Damk├Čhler number Ō£ż Code supplies both quantities Ō£ż Need to test if hypothesis holds Mixing Friday, April 30, 2010
- 31. The extinction ŌĆścriterionŌĆÖ Ō£ż The Damk├Čhler number Ō£ż Code supplies both quantities Ō£ż Need to test if hypothesis holds Mixing Chemistry Friday, April 30, 2010
- 32. What is new about this work? Friday, April 30, 2010
- 33. What is new about this work? Ō£ż Extinction studies with stretch -widely studied (Linan-1974) Friday, April 30, 2010
- 34. What is new about this work? Ō£ż Extinction studies with stretch -widely studied (Linan-1974) Ō£ż Extinction studies with heat losses (primarily, radiation) Friday, April 30, 2010
- 35. What is new about this work? Ō£ż Extinction studies with stretch -widely studied (Linan-1974) Ō£ż Extinction studies with heat losses (primarily, radiation) ŌĆó Some theoretical developments by TŌĆÖien, Law, Chao, Liu Friday, April 30, 2010
- 36. What is new about this work? Ō£ż Extinction studies with stretch -widely studied (Linan-1974) Ō£ż Extinction studies with heat losses (primarily, radiation) ŌĆó Some theoretical developments by TŌĆÖien, Law, Chao, Liu Ō£ż Current study Friday, April 30, 2010
- 37. What is new about this work? Ō£ż Extinction studies with stretch -widely studied (Linan-1974) Ō£ż Extinction studies with heat losses (primarily, radiation) ŌĆó Some theoretical developments by TŌĆÖien, Law, Chao, Liu Ō£ż Current study ŌĆó Rigorous treatment of non-adiabatic environments (soot, radiation, water spray) Friday, April 30, 2010
- 38. What is new about this work? Ō£ż Extinction studies with stretch -widely studied (Linan-1974) Ō£ż Extinction studies with heat losses (primarily, radiation) ŌĆó Some theoretical developments by TŌĆÖien, Law, Chao, Liu Ō£ż Current study ŌĆó Rigorous treatment of non-adiabatic environments (soot, radiation, water spray) ŌĆó Theoretical developments validated with high quality numerical datasets Friday, April 30, 2010
- 39. What is new about this work? Ō£ż Extinction studies with stretch -widely studied (Linan-1974) Ō£ż Extinction studies with heat losses (primarily, radiation) ŌĆó Some theoretical developments by TŌĆÖien, Law, Chao, Liu Ō£ż Current study ŌĆó Rigorous treatment of non-adiabatic environments (soot, radiation, water spray) ŌĆó Theoretical developments validated with high quality numerical datasets ŌĆó Questions asked about soot leakage and connection with radiative extinction Friday, April 30, 2010
- 40. What is new about this work? Ō£ż Extinction studies with stretch -widely studied (Linan-1974) Ō£ż Extinction studies with heat losses (primarily, radiation) ŌĆó Some theoretical developments by TŌĆÖien, Law, Chao, Liu Ō£ż Current study ŌĆó Rigorous treatment of non-adiabatic environments (soot, radiation, water spray) ŌĆó Theoretical developments validated with high quality numerical datasets ŌĆó Questions asked about soot leakage and connection with radiative extinction ŌĆó Treatment of radiation absorption (with possible extension to optically thick media) Friday, April 30, 2010
- 41. What is new about this work? Friday, April 30, 2010
- 42. Pulications Ō£ż Radiation driven ’¼éame weakening effects in sooting turbulent ’¼éames (2008), Narayanan & Trouv├®, ŌĆØProceedings of the combustion instituteŌĆØ Ō£ż Effects of soot addition on extinction limits of luminous laminar counter’¼éow ’¼éames, Narayanan, Baum & Trouv├® (Accepted, Combustion symposium, 2010) Ō£ż Extinction of Nonpremixed Ethylene-Air ’¼éames by water spray, Arias, Im, Narayanan & Trouv├® (Accepted, Combustion symposium, 2010) Ō£ż Mixture fraction and state relationships in diffusion ’¼éames interacting with an evaporating water spray, Narayanan, Trouv├®, Arias & Im (in preparation, presented at the US Combustion meeting, Ann Arbor, 2009) Ō£ż Constructing extinction maps for diffusion ’¼éames predicated by radiation emission in sooting turbulent ’¼éames, Narayanan, Lecoustre & Trouv├® (in preparation, presented at the International Seminar on Fire and Explosions Hazards, Leeds, 2010) Friday, April 30, 2010
- 43. Tools/approach Friday, April 30, 2010
- 44. Tools/approach Ō£ż Direct numerical simulations to generate datasets ŌĆó Massively parallel Combustion solver S3D ŌĆó NERSC machines (Franklin,Hopper) Friday, April 30, 2010
- 45. Tools/approach Ō£ż Direct numerical simulations to generate datasets ŌĆó Massively parallel Combustion solver S3D ŌĆó NERSC machines (Franklin,Hopper) Ō£ż Mathematical modeling ŌĆó Canonical problems solved using singular perturbation techniques Friday, April 30, 2010
- 46. Tools/approach Ō£ż Direct numerical simulations to generate datasets ŌĆó Massively parallel Combustion solver S3D ŌĆó NERSC machines (Franklin,Hopper) Ō£ż Mathematical modeling ŌĆó Canonical problems solved using singular perturbation techniques Ō£ż Model validation and analysis Friday, April 30, 2010
- 47. Numerical approach Friday, April 30, 2010
- 48. Numerical approach Ō£ż Use Direct numerical simulations (DNS) Friday, April 30, 2010
- 49. Numerical approach Ō£ż Use Direct numerical simulations (DNS) Ō£ż Leverage DOE sponsored SciDac collaboration solver S3D ŌĆó Collaborators: Sandia Ntl. Laboratories (J. J. Chen), University of Michigan (H. G. Im) Friday, April 30, 2010
- 50. Numerical approach Ō£ż Use Direct numerical simulations (DNS) Ō£ż Leverage DOE sponsored SciDac collaboration solver S3D ŌĆó Collaborators: Sandia Ntl. Laboratories (J. J. Chen), University of Michigan (H. G. Im) Ō£ż DNS solver S3D Ō£ō Navier-stokes solver; fully compressible ’¼éow formulation Ō£ō Higher-order methods: 8th order ’¼ünite difference; 4th order Runge Kutta time Ō£ō Characteristic based boundary conditions (NSCBC) Ō£ō Structured cartesian grids Ō£ō Parallel, MPI based (excellent scalability) Ō£ō Flame modeling: detailed fuel-air chemistry (CHEMKIN compatible); simpli’¼üed soot formation model; thermal radiation model (Discrete Ordinate/Discrete Transfer Method); Lagrangian particle model to describe dilute liquid sprays Friday, April 30, 2010
- 51. Flame modeling Friday, April 30, 2010
- 52. Single step chemistry Ō£ż Ethylene-air chemistry model (Westbrook & Dryer, 1981) Ō£ż Used for simpli’¼üed extinction model (in asymptotic analysis and numerical validation with DNS) Ōé¼ ╦ÖŽēF = BRR ( ŽüYF MF )╬Į F ( ŽüYO2 MF )╬ĮO exp(ŌłÆ Ta T ) Friday, April 30, 2010
- 53. Detailed Chemistry Ō£ż Used for more detailed calculations with water spray Ō£ż Reduced chemical kinetic mechanism (Lu & Law, 2009, Progress in Energy and Combustion Science) ŌĆó Based on detailed chemistry mechanism for ethylene-air combustion (70 species, 463 elementary reactions, Wang et al., 2000, Proceedings of the Combustion Institute) ŌĆó Reduced chemistry mechanism using: the method of directed relations graphs (DRG): sensitivity analysis; quasi steady-state assumption for fast reacting radicals ŌĆó 19 species, 15 semi-global reactions Friday, April 30, 2010
- 54. Soot formation model Ō£ż Phenomenological, two equation model (Moss et al., Lindstedt et al.) Ō£ż Soot formation process included into phenomenology ŌĆó nucleation, surface growth, coagulation, oxidation Friday, April 30, 2010
- 55. Lagrangian spray model Ō£ż Adapted from ŌĆśWang and RutlandŌĆś (2007), Combustion and Flame Ō£ż Spherical, monodisperse droplets Ō£ż ŌĆśParticle in cellŌĆÖ Ō£ż Dilute liquid phase assumption Ō£ż Lagrangian-Eulerian coupling Position Mass Momentum Energy Lagrangian droplet equations Droplet source terms in Eulerian gas equations Mass Momentum Energy Friday, April 30, 2010
- 56. Thermal radiation model Ō£ż Non-scattering, gray gas assumption; Discrete Transfer Method (Lockwood & Shah, 1981) Ō£ż Solve radiative transfer equation ŌĆó Mean absorption coef’¼ücient (ap,i) Friday, April 30, 2010
- 57. Problems investigated Friday, April 30, 2010
- 58. Problems investigated Ō£ż Turbulent sooting/radiating wall ’¼éames Friday, April 30, 2010
- 59. Problems investigated Ō£ż Turbulent sooting/radiating wall ’¼éames ŌĆó Radiative weakening and extinction ’¼ürst come to light in turbulent simulation Friday, April 30, 2010
- 60. Problems investigated Ō£ż Turbulent sooting/radiating wall ’¼éames ŌĆó Radiative weakening and extinction ’¼ürst come to light in turbulent simulation Ō£ż Laminar counter’¼éow sooting/radiating ’¼éames Friday, April 30, 2010
- 61. Problems investigated Ō£ż Turbulent sooting/radiating wall ’¼éames ŌĆó Radiative weakening and extinction ’¼ürst come to light in turbulent simulation Ō£ż Laminar counter’¼éow sooting/radiating ’¼éames ŌĆó Attempts in understanding radiative extinction through asymptotic analysis and numerical simulations Friday, April 30, 2010
- 62. Problems investigated Ō£ż Turbulent sooting/radiating wall ’¼éames ŌĆó Radiative weakening and extinction ’¼ürst come to light in turbulent simulation Ō£ż Laminar counter’¼éow sooting/radiating ’¼éames ŌĆó Attempts in understanding radiative extinction through asymptotic analysis and numerical simulations Ō£ż Turbulent counter’¼éow ’¼éames weakened by water spray Friday, April 30, 2010
- 63. Problems investigated Ō£ż Turbulent sooting/radiating wall ’¼éames ŌĆó Radiative weakening and extinction ’¼ürst come to light in turbulent simulation Ō£ż Laminar counter’¼éow sooting/radiating ’¼éames ŌĆó Attempts in understanding radiative extinction through asymptotic analysis and numerical simulations Ō£ż Turbulent counter’¼éow ’¼éames weakened by water spray ŌĆó More complex problem with detailed chemistry, explored via numerical simulations and application of asymptotic model developed Friday, April 30, 2010
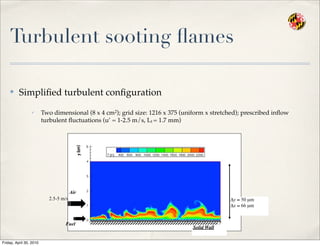
- 64. Turbulent sooting ’¼éames Ō£ż Simpli’¼üed turbulent con’¼üguration Ō£ō Two dimensional (8 x 4 cm2); grid size: 1216 x 375 (uniform x stretched); prescribed in’¼éow turbulent ’¼éuctuations (uŌĆÖ = 1-2.5 m/s, Lt = 1.7 mm) Air Fuel Solid Wall 2.5-5 m/s ╬öy Ōēł 50 ┬Ąm ╬öx Ōēł 66 ┬Ąm Friday, April 30, 2010
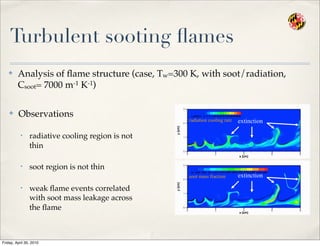
- 65. Turbulent sooting ’¼éames Ō£ż Observations ŌĆó radiative cooling region is not thin ŌĆó soot region is not thin ŌĆó weak ’¼éame events correlated with soot mass leakage across the ’¼éame radiation cooling rate soot mass fraction extinction extinction Ō£ż Analysis of ’¼éame structure (case, Tw=300 K, with soot/radiation, Csoot= 7000 m-1 K-1) Friday, April 30, 2010
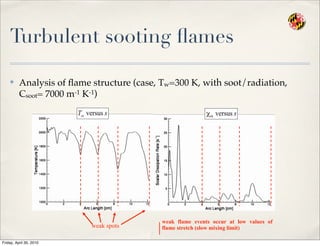
- 66. Turbulent sooting ’¼éames Ō£ż Analysis of ’¼éame structure (case, Tw=300 K, with soot/radiation, Csoot= 7000 m-1 K-1) weak spots weak flame events occur at low values of flame stretch (slow mixing limit) Friday, April 30, 2010
- 67. Radiative extinction under external soot loading Friday, April 30, 2010
- 68. Overview Ō£ż Explore connection between ’¼éame extinction and soot leakage ŌĆó Relevance in radiating/sooting environments Ō£ō Pool’¼üres ŌĆó Connection with smoking candle ’¼éames Cold Soot Hot Soot Friday, April 30, 2010
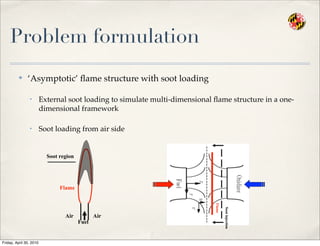
- 69. Problem formulation Ō£ż ŌĆśAsymptoticŌĆÖ ’¼éame structure with soot loading ŌĆó External soot loading to simulate multi-dimensional ’¼éame structure in a one- dimensional framework ŌĆó Soot loading from air side Fuel Air Air Flame Soot region Flame Sootinjection Friday, April 30, 2010
- 70. Problem formulation Ō£ż Approach: setup counter’¼éow ’¼éame with radiative heat loss ŌĆó Analytical setup (transform to one-dimensional scalar ’¼üelds) ŌĆó Numerical setup (DNS) for validation (two dimensional counter’¼éow ’¼éame) Ō£ż Outputs: Flame structure (’¼éame variables such as temperature, mixing rate, radiation cooling rate) Ō£ż Effect of soot loading on extinction properties ŌĆó how are the limits changed with radiation heat loss? Friday, April 30, 2010
- 71. ŌĆśActivation Energy AsymptoticsŌĆÖ Ō£ż Convert governing equations into one-dimensional coordinates using Howarth transformation for variable density Ō£ż Constant speci’¼üc heat, single step Arrhenius Chemistry Ō£ż Conventional solution using singular perturbation: split domain into ŌĆó Outer radiating zone-to obtain radiation corrected outer temperatures Ō£ō Full treatment-both emission and absorption handled (radiation transport equation solved) ŌĆó Inner reacting zone -complete ’¼éame structure and extinction conditions Ō£ō Solve using two point BVP solver ŌĆó Patch outer and inner solutions to obtain complete ’¼éame structure ŌĆó Solve for soot ’¼üeld using completed ’¼éame structure with BVP solver (but do not have bene’¼üt of asymptotic expansions here!) Outer Outer Inner Friday, April 30, 2010
- 72. Governing equations Only contributes near thin reaction zone (inner region) Zero far from reaction zone (outer region) Fuel (Ethylene) Outer layer (radiatively active) Thin ’¼éame (inner layer) Oxidizer (air) Friday, April 30, 2010
- 73. Outer solutions Ō£ż Solve for leading order solutions ŌĆ£farŌĆØ from ’¼éame Algorithm Ō£ōSolve on either side of ’¼éame using GreenŌĆÖs functions Ō£ōGet temperature at ’¼éame location Ō£ōSolve Inner equation Ō£ōObtain complete solution Howarth Transform Friday, April 30, 2010
- 74. Inner solutions Ō£ż Solve for inner solutions by ŌĆśzooming inŌĆÖ at ’¼éame zone Ō£ż Transform Outer Outer Inner Friday, April 30, 2010
- 75. Inner solutions Ō£ż Solve for inner solutions by ŌĆśzooming inŌĆÖ at ’¼éame zone Ō£ż Transform Outer Outer Inner Reduced Damk├Čhler number Friday, April 30, 2010
- 76. What is the effect of radiation in all this? Ō£ż Radiation free ’¼éame: (outer) temperature is the adiabatic ’¼éame temperature Ō£ż With radiation: (outer) temperature is lowered! Ō£ż Effects of radiation felt when ŌĆó Large amounts of soot ŌĆó Small strain Ō£ż Radiation corrected ’¼éame temperature feeds into inner equation Radiation correction to give new ŌĆ£Burke-SchumannŌĆØ temperature Text Solve RTE Friday, April 30, 2010
- 77. What is the effect of radiation in all this? Ō£ż Radiation free ’¼éame: (outer) temperature is the adiabatic ’¼éame temperature Ō£ż With radiation: (outer) temperature is lowered! Ō£ż Effects of radiation felt when ŌĆó Large amounts of soot ŌĆó Small strain Ō£ż Radiation corrected ’¼éame temperature feeds into inner equation Radiation correction to give new ŌĆ£Burke-SchumannŌĆØ temperature Radiation Text Solve RTE Friday, April 30, 2010
- 78. What is the effect of radiation in all this? Ō£ż Radiation free ’¼éame: (outer) temperature is the adiabatic ’¼éame temperature Ō£ż With radiation: (outer) temperature is lowered! Ō£ż Effects of radiation felt when ŌĆó Large amounts of soot ŌĆó Small strain Ō£ż Radiation corrected ’¼éame temperature feeds into inner equation Radiation correction to give new ŌĆ£Burke-SchumannŌĆØ temperature Radiation Strain Text Solve RTE Friday, April 30, 2010
- 79. On radiative emission and absorption Ō£ż Emission: local function of temperature Ō£ż Absorption: non-local convolution integral ŌĆó Depends on optical thickness of surroundings ŌĆó Can develop asymptotic measures for radiating regimes (ŌĆśthickŌĆÖ (Szoke, LLNL), ŌĆśthinŌĆÖ (the optically thin assumption), ŌĆśintermediateŌĆÖ) ŌĆó Possibilities of regime based approximations (thick and thin somewhat amenable to analytical solutions (!?), intermediate needs computation) Radiation source term Optically thin Optically thick Friday, April 30, 2010
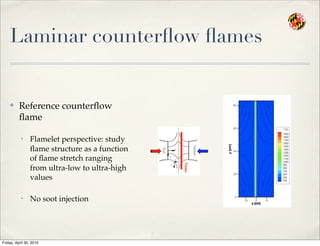
- 80. Laminar counter’¼éow ’¼éames Ō£ż Reference counter’¼éow ’¼éame ŌĆó Flamelet perspective: study ’¼éame structure as a function of ’¼éame stretch ranging from ultra-low to ultra-high values ŌĆó No soot injection Flame Friday, April 30, 2010
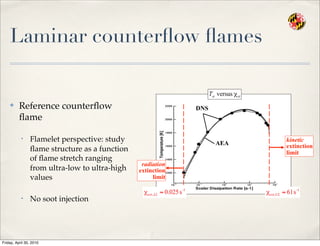
- 81. Laminar counter’¼éow ’¼éames Ō£ż Reference counter’¼éow ’¼éame ŌĆó Flamelet perspective: study ’¼éame structure as a function of ’¼éame stretch ranging from ultra-low to ultra-high values ŌĆó No soot injection kinetic extinction limit radiation extinction limit DNS AEA Friday, April 30, 2010
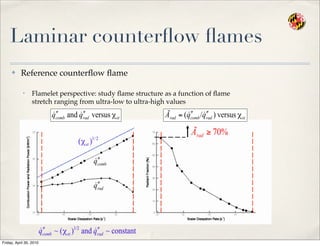
- 82. Laminar counter’¼éow ’¼éames Ō£ż Reference counter’¼éow ’¼éame ŌĆó Flamelet perspective: study ’¼éame structure as a function of ’¼éame stretch ranging from ultra-low to ultra-high values Friday, April 30, 2010
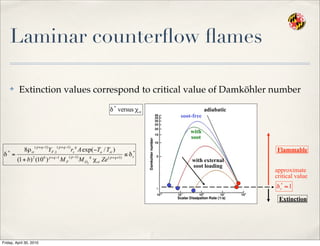
- 83. Laminar counter’¼éow ’¼éames Ō£ż Extinction values correspond to critical value of Damk├Čhler number Friday, April 30, 2010
- 84. Laminar counter’¼éow ’¼éames Ō£ż Extinction values correspond to critical value of Damk├Čhler number adiabatic soot-free with soot with external soot loading approximate critical value Extinction Flammable Friday, April 30, 2010
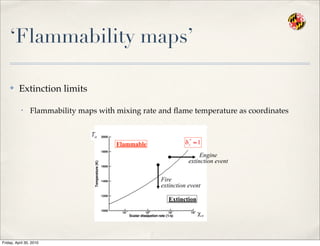
- 85. ŌĆśFlammability mapsŌĆÖ Ō£ż Extinction limits ŌĆó Flammability maps with mixing rate and ’¼éame temperature as coordinates Extinction Flammable Engine extinction event Fire extinction event Friday, April 30, 2010
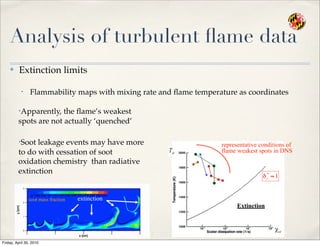
- 86. Analysis of turbulent ’¼éame data Ō£ż Extinction limits ŌĆó Flammability maps with mixing rate and ’¼éame temperature as coordinates Extinction representative conditions of flame weakest spots in DNS ŌĆóApparently, the ’¼éameŌĆÖs weakest spots are not actually ŌĆśquenchedŌĆÖ ŌĆóSoot leakage events may have more to do with cessation of soot oxidation chemistry than radiative extinction soot mass fraction extinction Friday, April 30, 2010
- 87. Conclusions on sooting ’¼éames Friday, April 30, 2010
- 88. Conclusions on sooting ’¼éames Ō£ż Activation energy asymptotics and DNS have been used to make fundamental observations on non-adiabatic turbulent sooting diffusion ’¼éames Friday, April 30, 2010
- 89. Conclusions on sooting ’¼éames Ō£ż Activation energy asymptotics and DNS have been used to make fundamental observations on non-adiabatic turbulent sooting diffusion ’¼éames Ō£ż Two extinction limits are encountered ŌĆó Kinetic extinction (at high stretch) ŌĆó Radiative extinction (at low stretch) Friday, April 30, 2010
- 90. Conclusions on sooting ’¼éames Ō£ż Activation energy asymptotics and DNS have been used to make fundamental observations on non-adiabatic turbulent sooting diffusion ’¼éames Ō£ż Two extinction limits are encountered ŌĆó Kinetic extinction (at high stretch) ŌĆó Radiative extinction (at low stretch) Ō£ż Extinction occurs at a single critical value of the ŌĆśreducedŌĆÖ Damk├Čhler number equalling unity ŌĆó Can construct maps to gauge extinction propensity of ’¼éames Friday, April 30, 2010
- 91. Conclusions on sooting ’¼éames Ō£ż Activation energy asymptotics and DNS have been used to make fundamental observations on non-adiabatic turbulent sooting diffusion ’¼éames Ō£ż Two extinction limits are encountered ŌĆó Kinetic extinction (at high stretch) ŌĆó Radiative extinction (at low stretch) Ō£ż Extinction occurs at a single critical value of the ŌĆśreducedŌĆÖ Damk├Čhler number equalling unity ŌĆó Can construct maps to gauge extinction propensity of ’¼éames Ō£ż Turbulent ’¼éame data indicate that soot leakage events are not necessarily radiative extinction events. Further investigation of soot oxidation chemistry is warranted Friday, April 30, 2010
- 92. DNS of turbulent spray ’¼éames Friday, April 30, 2010
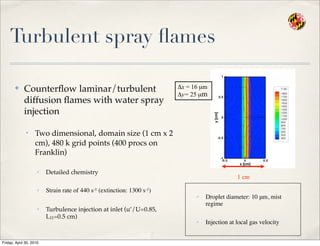
- 93. Turbulent spray ’¼éames Ō£ż Counter’¼éow laminar/turbulent diffusion ’¼éames with water spray injection ŌĆó Two dimensional, domain size (1 cm x 2 cm), 480 k grid points (400 procs on Franklin) Ō£ō Detailed chemistry Ō£ō Strain rate of 440 s-1 (extinction: 1300 s-1) Ō£ō Turbulence injection at inlet (uŌĆÖ/U=0.85, L11=0.5 cm) 1 cm ╬öx = 16 ┬Ąm ╬öy= 25 ┬Ąm Ō£ō Droplet diameter: 10 ╬╝m, mist regime Ō£ō Injection at local gas velocity Friday, April 30, 2010
- 94. Unexplored areas Ō£ż Extinction and soot leakage ŌĆó If soot leakage precedes radiative extinction, can one come up with a description based on soot chemistry Ō£ō ŌĆśDamk├ČhlerŌĆÖ number criterion for cessation of soot oxidation chemistry ŌĆó Could have rami’¼ücations in smoking ’¼üres Ō£ō Strongly radiating, but not quenched Ō£ż Development of approximations in thick media (and thin) and its application to radiating solvers ŌĆó Envisage cost reduction if only ŌĆśintermediateŌĆÖ regions need to be computed Ō£ż How do we incorporate chemistry effects in complex ’¼éames? Friday, April 30, 2010