Lect 5
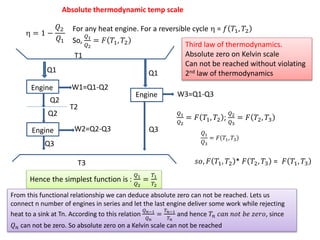
- 1. Absolute thermodynamic temp scale ïĻ = 1 â ð2 ð1 For any heat engine. For a reversible cycle ïĻ = ð ð1, ð2 So, ð1 ð2 = ðđ ð1, ð2 T1 T2 Q1 Q2 Q2 Q3 T3 W1=Q1-Q2 W2=Q2-Q3 Q1 Q3 W3=Q1-Q3 ð1 ð2 = ðđ ð1, ð2 ; ð2 ð3 = ðđ ð2, ð3 ð1 ð3 = ðđ ð1, ð3 ð ð, ðđ ð1, ð2 * ðđ ð2, ð3 = ðđ ð1, ð3 Hence the simplest function is : ð1 ð2 = ð1 ð2 From this functional relationship we can deduce absolute zero can not be reached. Lets us connect n number of engines in series and let the last engine deliver some work while rejecting heat to a sink at Tn. According to this relation ð ðâ1 ð ð = ð ðâ1 ð ð and hence ðð ððð ðððĄ ðð ð§ððð, since ð ð can not be zero. So absolute zero on a Kelvin scale can not be reached Third law of thermodynamics. Absolute zero on Kelvin scale Can not be reached without violating 2nd law of thermodynamics Engine Engine Engine
- 2. ïĻ = 1 â ð2 ð1 = 1 â ð2 ð1 Efficiency of reversible heat engine ððð ref = Q2 Q1 â Q2 = T2 T1 â T2 ððð HP = Q1 Q1 â Q2 = T1 T1 â T2 Internally reversible and externally irreversible process TH TL QH QL Ta Tb Engine W ð ðŧ = ð ðŧ(ð ðŧ â ðð) ð ðŋ = ð ðŋ(ðð â ððŋ) ð = ð ðŧ â ð ðŋ If ð ðŧ â ðð and ðð = ððŋ then ïĻ is max But QH=0 and w=0 On the other hand if ðð ⊠ð ðŧ, ððð ðð âŦ ððŋ ð ðŧ âŦ 0, ïĻ â 0, ððð ðĪ â 0 So there is some optimal set of cycle temp for maximum power output. Find optimum ðð ððð ððfor max power. Known are: ðķ ðŧ, ðķðŋ, ð ðŧ, ððŋ ððð ðĒðððððĪð ððð ðð ððð ðð, find max W ch=100; cl=80; th=900; tl=300 qh=ch*(th-ta) ql=cl*(tb-tl) w=qh-ql qh/ta=ql/tb ta_theo=ch/(ch+cl)*th+cl/(ch+cl)*sqrt(th*tl) tb_theo=cl/(ch+cl)*tl+ch/(ch+cl)*sqrt(th*tl) Make a parametric table with Ta, Tb, Qh, QL, and w Vary Ta from 900 to 630K and get the table solved. Now you can see W as a function of Ta and Tb. Find W_max from the table.