Lect 7 thermo
- 1. Maximum work or available energy from a system Initially a body of mass m, is at temp T, what is the maximum work that can be obtained out of it if the environment is at π0 which is lower than the body temperature T. π0 πβ ππ w ππ π£ π πβ = ππ π£ π β π0 ; βπ π = ππ π£ ln π0 π βπ π π’π = ππ/π0 For max work output, βπ π π’π + βπ π = 0 ππ = βπ0 π π π£ ln π0 π ; π€ = πβ β ππ = ππ π£ π β π0 β π0 ππ π£ ln π π0 π€ = ππ π£ π β π0 β π0 ln π π0 = π1 β π0 β π0(π1 β π0) = π1 β π0 π1 β π0 β π0 π0 = πΉ1 β πΉ0; π€βπππ πΉ = π β π0 π, πΉ ππ ππππππ π‘βπ ππ£πππππππππ‘π¦ ππ π»ππππππ‘π§ ππ’πππ‘πππ If the system boundary expands against the atmospheric pressure p0 then F becomes: π = π β π0 π + π0 π, π1 β π2 = ππ£πππππππ π€πππ = π€ πππ₯
- 2. cm π0 π12 π0 w12 πβ Control mass process when the system receives heat from a source Maximum work or available energy π1 β π2 π1 β π2 The system goes from 1-2, does work w12 and rejects heat π0 Lets us consider two situations: the body rejects heat either reversibly or irreversibly, but it receives heat reversibly. π12 β π0 πππ = π2 β π1 + π€12 πππ‘ π πππ = βπ ππ + βπ π π’π + βπ πππ > 0, for irrev process π πππ πππ£ = π2 β π1 + π0 πππ£ π0 β π12 πβ = 0 for rev process π0 πππ£ = βπ0 π2 β π1 + π0 πβ Q12, From 1st law for the CM we get: π12 β π0 πππ£ = π€12 πππ£ + π2 β π1 π€12 πππ£ = π12 β π0 πππ£ β π2 β π1 π€12 πππ£ = π12 + π0 π2 β π1 β π12 π0 πβ β π2 β π1 π€12 πππ£ = π12 1 β π0 πβ + π1 β π0 π1 β π2 β π0 π2 π€12 πππ£ = π€ πππ₯ = π12 1 β π0 πβ + πΉ1 β πΉ2 sur res π€12 πππ‘ = π12 β π0 πππ β π2 β π1 πΌ = πΌππ = π€12 πππ£ β π€12 πππ‘ = π0 π2 β π1 β π12 π0 πβ + π0 πππ = π0 π2 β π1 β π12 πβ + π0 πππ π0 = π0(βπ ππ + βπ πππ + βπ π π’π) = π0βπ π’πππ£ = π0 π πππ Measure of irreversibility
- 3. NH3 100C Example problem: 1kg of NH3 is contained in a spring loaded piston/cylinder as saturated liquid at -20C. Heat is added from a reservoir at 100C until a final state of 800kpa, 70C is reached. Find the work, heat transfer, and entropy generation assuming the process to be internally reversible. p1=pressure(r717,t=-20,x=0) v1=volume(r717,t=-20,x=0) u1=intenergy(r717,t=-20,x=0) s1=entropy(r717,t=-20,x=0) v2=volume(r717,p=800,t=70) u2=intenergy(r717,t=70,p=800) s2=entropy(r717,t=70,p=800) w12=(800+p1)*.5*(v2-v1) q12=w12+u2-u1 s_gen+q12/373=s2-s1
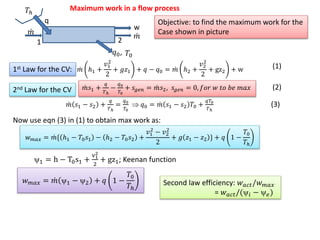
- 4. Maximum work in a flow process 1 2 w π π q πβ π0π0, Objective: to find the maximum work for the Case shown in picture 1st Law for the CV: π β1 + π£1 2 2 + ππ§1 + π β π0 = π β2 + π£2 2 2 + gz2 + w ππ 1 + π πβ β π0 π0 + π πππ = ππ 2, π πππ = 0, πππ π€ π‘π ππ πππ₯2nd Law for the CV π π 1 β π 2 + π πβ = π0 π0 ο π0 = π π 1 β π 2 π0 + ππ0 πβ (1) (2) Now use eqn (3) in (1) to obtain max work as: (3) π€ πππ₯ = π{ β1 β π0 π 1 β β2 β π0 π 2 + π£1 2 β π£2 2 2 + π π§1 β π§2 } + π 1 β π0 πβ οΉ1 = h β T0s1 + v1 2 2 + gz1; Keenan function π€ πππ₯ = π οΉ1 β οΉ2 + π 1 β π0 πβ Second law efficiency: π€ πππ‘/π€ πππ₯ = π€ πππ‘/(οΉπ β οΉ π)
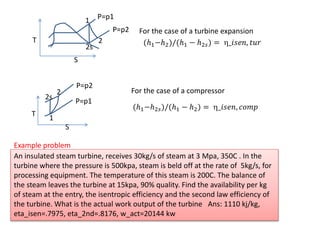
- 5. T S 1 2 2s P=p1 P=p2 (β1ββ2)/(β1 β β2π ) = ο¨_ππ ππ, π‘π’π For the case of a turbine expansion P=p2 1 2s 2 T S P=p1 For the case of a compressor (β1ββ2π )/(β1 β β2) = ο¨_ππ ππ, ππππ An insulated steam turbine, receives 30kg/s of steam at 3 Mpa, 350C . In the turbine where the pressure is 500kpa, steam is beld off at the rate of 5kg/s, for processing equipment. The temperature of this steam is 200C. The balance of the steam leaves the turbine at 15kpa, 90% quality. Find the availability per kg of steam at the entry, the isentropic efficiency and the second law efficiency of the turbine. What is the actual work output of the turbine Ans: 1110 kj/kg, eta_isen=.7975, eta_2nd=.8176, w_act=20144 kw Example problem
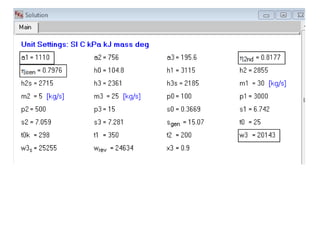
- 6. m1=30 [kg/s]; m2= 5[kg/s]; m3=25 [kg/s] p1=3000; p2=500; p3=15; x3=.9; p0=100 t1= 350; t2=200; t0=25; t0k=298 h1=enthalpy(steam,p=p1,t=t1) s1=entropy(steam,p=p1,t=t1) h0=enthalpy(water,p=p0,t=t0) s0=entropy(water,p=p0,t=t0) h2=enthalpy(steam,p=p2,t=t2) s2=entropy(steam,p=p2,t=t2) h3=enthalpy(steam,p=p3,x=x3) s3=entropy(steam,p=p3,x=x3) a1=h1-t0k*s1-(h0-t0k*s0) { availability at entry} a2=h2-t0k*s2-(h0-t0k*s0) a3=h3-t0k*s3-(h0-t0k*s0) m1*h1=m2*h2+m3*h3+w3 { w3 = actual work output} m1*s1+s_gen=m2*s2+m3*s3 w_rev=w3+t0k*s_gen eta_2nd=w3/w_rev h2s=enthalpy(steam,p=p2,s=s1) h3s=enthalpy(steam,p=p3,s=s1) m1*h1=m2*h2s+m3*h3s+w3_s {w3s = isentropic work of turbine} eta_isen=w3/w3_s 30kg/s 3MPa, 350C 5kg/s .5MPa, 200C 25kg/s 15kPa, 90%quality 1 2 3 π€cv



![m1=30 [kg/s]; m2= 5[kg/s]; m3=25 [kg/s]
p1=3000; p2=500; p3=15; x3=.9; p0=100
t1= 350; t2=200; t0=25; t0k=298
h1=enthalpy(steam,p=p1,t=t1)
s1=entropy(steam,p=p1,t=t1)
h0=enthalpy(water,p=p0,t=t0)
s0=entropy(water,p=p0,t=t0)
h2=enthalpy(steam,p=p2,t=t2)
s2=entropy(steam,p=p2,t=t2)
h3=enthalpy(steam,p=p3,x=x3)
s3=entropy(steam,p=p3,x=x3)
a1=h1-t0k*s1-(h0-t0k*s0) { availability at entry}
a2=h2-t0k*s2-(h0-t0k*s0)
a3=h3-t0k*s3-(h0-t0k*s0)
m1*h1=m2*h2+m3*h3+w3 { w3 = actual work output}
m1*s1+s_gen=m2*s2+m3*s3
w_rev=w3+t0k*s_gen
eta_2nd=w3/w_rev
h2s=enthalpy(steam,p=p2,s=s1)
h3s=enthalpy(steam,p=p3,s=s1)
m1*h1=m2*h2s+m3*h3s+w3_s {w3s = isentropic work of turbine}
eta_isen=w3/w3_s
30kg/s
3MPa, 350C
5kg/s
.5MPa, 200C
25kg/s
15kPa, 90%quality
1
2
3
π€cv](https://image.slidesharecdn.com/lect7-150420145113-conversion-gate01/85/Lect-7-thermo-6-320.jpg)