�ݺ�ߣ

Computer Science Division: CS301
Course CS301, Part:
“ALGORITHMIC COMBINATORICS I”
( 3rd Year Students )
Prepared by:
http://www.researchgate.net/profile/Ahmed_Abdel-Fattah
Lecture #2
Dr. Ahmed Ashry “Algorithmic Combinatorics I” for 3rd Year Students — Lecture #2 1 (of 16)

The ZEROTH Laws of Counting:
The 1st 0th law of counting: The Sum Principle
Disjunction leads to addition: add exclusive options.
If there are ri different objects in the i th set, for 1 ! i ! m, and if the
different m sets are disjoint, then the number of ways to select an object
from (one of) the m sets is
m
!i=1
ri .
The 2nd 0th law of counting: The Product Principle
Conjunction leads to multiplication: multiply successive choices or actions.
For a counting procedure that is decomposable into m successive
(ordered) stages, with distinct ri outcomes in the i th stage, for
1 ! i ! m, then the total procedure has
m
"i=1
ri different composite
outcomes, provided that the composite outcomes are all distinct.

The FIRST Laws of Counting:
Simple Selections and Arrangements:
An r-combination of n distinct objects is an unordered selection of r of the n objects.
C(n, r) =
n!
r! (n − r )!
= !n
r"
An r-permutation of n distinct objects is an arrangement of r out of the n objects.
P(n, r) =
n!
(n − r )!
Example:
How many 4-digit numbers with distinct digits can be formed from the
set of digits {1, 2, 3, 4, 5}?
Ans.:
Product rule: =" 5 × 4 × 3 × 2 = 120
P(n,r): =" P(5, 4) = 5!
(5−4)! = 5! = 120

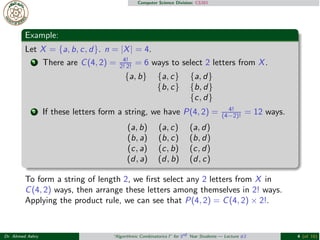
Example:
Let X = {a, b, c, d}. n = |X| = 4.
1 There are C(4, 2) = 4!
2! 2! = 6 ways to select 2 letters from X.
{a, b} {a, c} {a, d}
{b, c} {b, d}
{c, d}
2 If these letters form a string, we have P(4, 2) = 4!
(4−2)! = 12 ways.
(a, b) (a, c) (a, d)
(b, a) (b, c) (b, d)
(c, a) (c, b) (c, d)
(d, a) (d, b) (d, c)
To form a string of length 2, we first select any 2 letters from X in
C(4, 2) ways, then arrange these letters among themselves in 2! ways.
Applying the product rule, we can see that P(4, 2) = C(4, 2) × 2!.

Permutations of Non-Distinct Objects:
Theorem (The Mississippi Rule:a)
a([Tucker, 2007, Theorem 1, Page 187])
The number of permutations of n objects that consist of qi objects of the i th type,
for 1 ! i ! t, i.e. n =
t
!
i=1
qi, is given by:
P(n; q1, q2, . . . , qt) :=
n!
q1! × q2! × ·· ·×qt !
In how many ways can we arrange 3 dashes and 2 dots?
(Ans.) In P(5; 3, 2) =
(3 + 2)!
3! × 2!
= 10 ways (N.B. n = 5, q1 = 3, and q2 = 2).
What is the number of distinct permutations of “MISSISSIPPI”?
(Ans.) In P(11; 1, 4, 4, 2) =
11!
4! × 4! × 2!
= 34, 650 ways (N.B. n = 11, qM = 1, qI = 4, qS = 4,
and qP = 2).

Digression: Deal or No Deal?
Want to get your 6% of oral examination?
Here is the deal:
1 Form a team of 2 students [use: #FOSCS301 Team]
2 Select a (predefined) topic.
3 Take your time.
4 Prepare and present in (max.) 5 minutes/slides.
N.B. Only 13 topics. . . First come first served!

Digression: Coding Things
What’s an Octet?
An octeta is a unit of digital information in computing and
telecommunications that consists of eight bits. The term is often used
when the term byte might be ambiguous, as historically there was no
standard definition for the size of the byte.
a(Source: http://en.wikipedia.org/wiki/Octet_(computing))

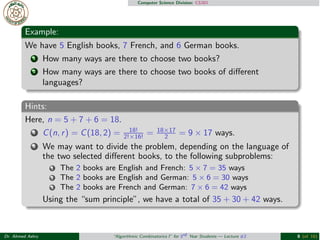
Example:
We have 5 English books, 7 French, and 6 German books.
1 How many ways are there to choose two books?
2 How many ways are there to choose two books of different
languages?
Hints:
Here, n = 5+7+6 = 18.
2!×16! = 18×17
2 = 9× 17 ways.
1 C(n, r) = C(18, 2) = 18!
2 We may want to divide the problem, depending on the language of
the two selected different books, to the following subproblems:
1 The 2 books are English and French: 5 ×7 = 35 ways
2 The 2 books are English and German: 5 ×6 = 30 ways
3 The 2 books are French and German: 7 ×6 = 42 ways
Using the “sum principle”, we have a total of 35 + 30 + 42 ways.

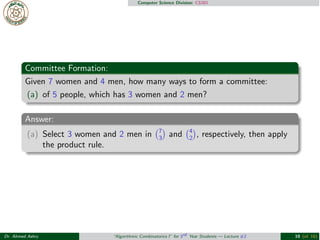
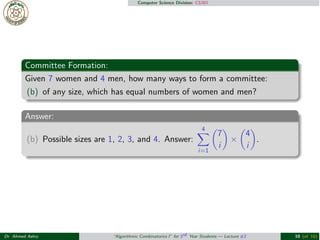
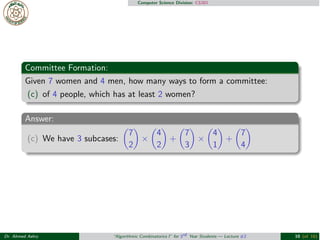
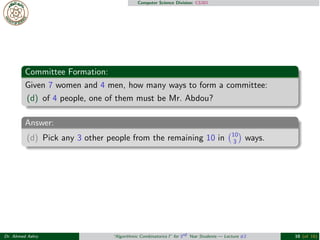
Group Formation:
Given 7 women and 4 men, how many ways to form a committee:
(a) of 5 people, which has 3 women and 2 men?
(b) of any size, which has equal numbers of women and men?
(c) of 4 people, which has at least 2 women?
(d) of 4 people, one of them must be Mr. Abdou?

Committee Formation:
(a) of 5 people, which has 3 women and 2 men?
Answer:
(a) Select 3 women and 2 men in #7
3$ and #4
2$, respectively, then apply
the product rule.

(b) of any size, which has equal numbers of women and men?
Answer:
(b) Possible sizes are 1, 2, 3, and 4. Answer:
4
!i=1
%7
i& × %4
i&.

(c) of 4 people, which has at least 2 women?
Answer:
(c) We have 3 subcases: %7
2& × %4
2& + %7
3& × %4
1& + %7
4&

(d) of 4 people, one of them must be Mr. Abdou?
Answer:
(d) Pick any 3 other people from the remaining 10 in #10
3 $ ways.

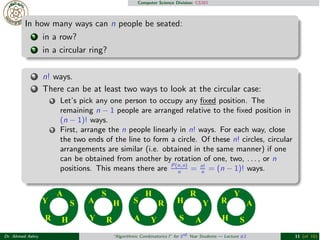
In how many ways can n people be seated:
1 in a row?
2 in a circular ring?
1 n! ways.
2 There can be at least two ways to look at the circular case:
1 Let’s pick any one person to occupy any fixed position. The
remaining n − 1 people are arranged relative to the fixed position in
(n − 1)! ways.
2 First, arrange the n people linearly in n! ways. For each way, close
the two ends of the line to form a circle. Of these n! circles, circular
arrangements are similar (i.e. obtained in the same manner) if one
can be obtained from another by rotation of one, two, . . . , or n
positions. This means there are P(n,n)
n = n!
n = (n − 1)! ways.

How many ways can 8 people sit in a circle if Omar and Salwa must sit
next to each other?
Hints:
Method 1: 1 Treat Omar and Salwa as a single unit, then arrange
7 units in a circle (6! ways).
2 There are 2 ways to place Omar and Salwa next to
each other.
3 Final answer: 6! × 2 = 1440 ways.
Method 2: 1 Seat Omar anywhere.
2 Seat Salwa adjacent to him (i.e. 2 ways).
3 Pick the remaining 6 people one at a time:
6 × 5 × 4 × 3 × 2 × 1.
4 Final answer: 2 × 6 × 5 × 4 × 3 × 2 ×1 = 1440 ways.
Exercise: What is the number of ways if Omar and Salwa refuse to sit next to each other?

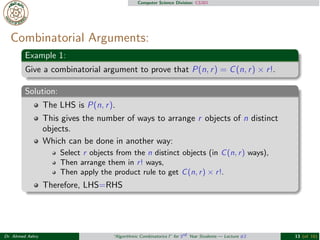
Combinatorial Arguments:
Example 1:
Give a combinatorial argument to prove that P(n, r) = C(n, r ) × r !.
Solution:
The LHS is P(n, r ).
This gives the number of ways to arrange r objects of n distinct
objects.
Which can be done in another way:
Select r objects from the n distinct objects (in C(n
,
r ) ways),
Then arrange them in r ! ways,
Then apply the product rule to get C(n
,
r ) × r !.
Therefore, LHS=RHS

Combinatorial Arguments:
Example 2:
Give a combinatorial argument to prove that C(n, r) = C(n, n − r ).
Solution:
The LHS gives the number of ways to form a subset of r objects of
n distinct objects.
This can be done in another way:
Select (n − r ) objects from the n distinct objects (in C(n
,
n − r )
ways), and exclude them.
The number of ways to construct a subset of r objects is equal to
the number of ways to select (n − r ) objects NOT to be included.
Therefore, LHS=RHS

Take Home Messages:
1 Bad news first: “Nothing alone is enough”
2 Divide and conquer: With Practice Comes
Mastery!
Homework #2:
1 Apply the Mississippi Rule to prove that (3n)! is divisible by 2n × 3n.
[Hint: think about permuting 3n non-distinct objects of n types]
2 Read and understand Example 4 ([Tucker, 2007, Page 175]).
3 Read and understand Example 6 ([Tucker, 2007, Page 176]).
4 Solve Exercises 11 ([Tucker, 2007, Page 181]).

References:
Tucker, A. (2007).
Applied combinatorics.
Wiley, 5th edition.

�ݺ�ߣ

Lecture #2: Algorithmic Combinatorics I "#FOSCS301"

More Related Content

Lecture #2: Algorithmic Combinatorics I "#FOSCS301"