LEXBFS on Chordal Graphs
•Download as PPTX, PDF•
0 likes•1,214 views
Cordal graphs are graphs where every cycle of 4 or more vertices has an edge connecting two non-adjacent vertices (a chord). There are three equivalent properties of cordal graphs: 1) they are chordal, 2) they have a perfect elimination ordering, and 3) minimal vertex separators induce complete subgraphs. The LEX BFS algorithm uses a lexicographic breadth-first search to find a perfect elimination ordering in polynomial time, identifying if a graph is cordal. It partitions the vertices into adjacent and non-adjacent sets at each step until all vertices are visited.
![Cordal Graphs [Triangulated Graphs]
• Definition. An undirected graph G is called Cordal-triangulated
if every cycle of length strictly greater than 3 possesses a
chord, that is, an edge joining two nonconsecutive vertices of
the cycle.
• For a graph G on n vertices, the following conditions
are equivalent:
• 1. G is chordal.
• 2.G has a perfect elimination ordering.
• 3. If H is any induced subgraph of G and S is a
vertex separator of H of minimal size, S’s vertices
induce a complete subgraph of G.](https://image.slidesharecdn.com/lexbfsoncordalgraphs-ppt-150513224017-lva1-app6892/85/LEXBFS-on-Chordal-Graphs-2-320.jpg)
![// Simplicial
• Definition. In a graph G, a vertex v is called simplicial if and only if the subgraph
(adjacency set) of G induced by the vertex set {v} ∪ N (v) is a complete graph. // a clique
(not necessarily maximal)]
• For example, in the graph below, vertex 3 is simplicial, while vertex 4 is not:
Vertex 3 Vertex4](https://image.slidesharecdn.com/lexbfsoncordalgraphs-ppt-150513224017-lva1-app6892/85/LEXBFS-on-Chordal-Graphs-4-320.jpg)
![Cordal Graphs [Triangulated Graphs]
• Definition. An undirected graph G is called Cordal-triangulated
if every cycle of length strictly greater than 3 possesses a
chord, that is, an edge joining two nonconsecutive vertices of
the cycle.
• For a graph G on n vertices, the following conditions
are equivalent:
• 1. G is chordal.
• 2.G has a perfect elimination ordering.
• 3. If H is any induced subgraph of G and S is a
vertex separator of H of minimal size, S’s vertices
induce a complete subgraph of G.](https://image.slidesharecdn.com/lexbfsoncordalgraphs-ppt-150513224017-lva1-app6892/85/LEXBFS-on-Chordal-Graphs-5-320.jpg)
LEXBFS on Chordal Graphs
- 1. CORDAL GRAPH Identification via Lex BFS Nazli Temur
- 2. Cordal Graphs [Triangulated Graphs] • Definition. An undirected graph G is called Cordal-triangulated if every cycle of length strictly greater than 3 possesses a chord, that is, an edge joining two nonconsecutive vertices of the cycle. • For a graph G on n vertices, the following conditions are equivalent: • 1. G is chordal. • 2.G has a perfect elimination ordering. • 3. If H is any induced subgraph of G and S is a vertex separator of H of minimal size, S’s vertices induce a complete subgraph of G.
- 3. Perfect Elimination Ordering A graph G on n vertices is said to have a perfect elimination ordering if and only if there is an ordering {v1, . . . vn} of G’s vertices, such that each vi is simplicial in the subgraph induced by the vertices {v1, . . . vi}. As an example, the graph above has a perfect elimination ordering, witnessed by the ordering (2, 1, 3, 4) of its vertices.
- 4. // Simplicial • Definition. In a graph G, a vertex v is called simplicial if and only if the subgraph (adjacency set) of G induced by the vertex set {v} ∪ N (v) is a complete graph. // a clique (not necessarily maximal)] • For example, in the graph below, vertex 3 is simplicial, while vertex 4 is not: Vertex 3 Vertex4
- 5. Cordal Graphs [Triangulated Graphs] • Definition. An undirected graph G is called Cordal-triangulated if every cycle of length strictly greater than 3 possesses a chord, that is, an edge joining two nonconsecutive vertices of the cycle. • For a graph G on n vertices, the following conditions are equivalent: • 1. G is chordal. • 2.G has a perfect elimination ordering. • 3. If H is any induced subgraph of G and S is a vertex separator of H of minimal size, S’s vertices induce a complete subgraph of G.
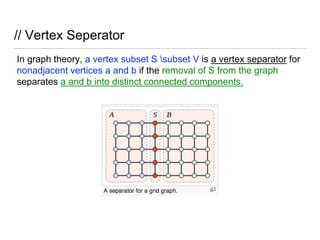
- 6. // Vertex Seperator In graph theory, a vertex subset S subset V is a vertex separator for nonadjacent vertices a and b if the removal of S from the graph separates a and b into distinct connected components.
- 7. Note : A graph with no or one nodes is connected. Sconnected component 2 connected component 1 3rd Condition If H is any induced subgraph of G and S is a vertex separator of H of minimal size, S’s vertices induce a complete subgraph of G. //induced subgraph is complete;
- 8. Cordal Graph Identification with LEX BFS Rose, Lueker & Tarjan (1976) (see also Habib et al. 2000) show that a perfect elimination ordering of a chordal graph may be found efficiently using an algorithm known as lexicographic breadth-first search.
- 9. LEX BFS on Cordal Graph Sigma(a) a N’(a)-adj Partitions L={2431} 1 2 3 4 5 • Vertices list is going be partitioned into two set P (Adj) and P’ (Non-Adj). • The next vertex will be chosen such that it has lexicographically largest label. • P’ is always located to the left most side of the Partitions List and will be processed first. • Any visited node will be removed from L=list. • LexBFS terminates since all vertices have been visited.
- 10. Sigma(a) a N’(a)-adj Partitions L={2431} 1 2 {1,4} {1,4} {3} 2 3 4 5 LEX BFS on Cordal Graph 2 is Removed • Vertices list is going be partitioned into two set P (Adj) and P’ (Non-Adj). • The next vertex will be chosen such that it has lexicographically largest label. • P’ is always located to the left most side of the Partitions List and will be processed first. • Any visited node will be removed from L=list. • LexBFS terminates since all vertices have been visited.
- 11. Sigma(a) a N’(a)-adj Partitions L={2431} 1 2 {1,4} {1,4} {3} 2 1 {4,3} {4} {3} 3 4 5 1&2 is Removed LEX BFS on Cordal Graph • Vertices list is going be partitioned into two set P (Adj) and P’ (Non-Adj). • The next vertex will be chosen such that it has lexicographically largest label. • P’ is always located to the left most side of the Partitions List and will be processed first. • Any visited node will be removed from L=list. • LexBFS terminates since all vertices have been visited.
- 12. Sigma(a) a N’(a)-adj Partitions L={2431} 1 2 {1,4} {1,4} {3} 2 1 {4,3} {4} {3} 3 4 {3} {3}{} 4 5 LEX BFS on Cordal Graph 1&2&4 are Removed • Vertices list is going be partitioned into two set P (Adj) and P’ (Non-Adj). • The next vertex will be chosen such that it has lexicographically largest label. • P’ is always located to the left most side of the Partitions List and will be processed first. • Any visited node will be removed from L=list. • LexBFS terminates since all vertices have been visited.
- 13. Sigma(a) a N’(a)-adj Partitions L={2431} 1 2 {1,4} {1,4} {3} 2 1 {4,3} {3}{4} 3 4 {3} {3}{} 4 3 {} {} 5 Terminate ALL is Removed LEX BFS on Cordal Graph Sigma(a)=(2,1,4,3) • Vertices list is going be partitioned into two set P (Adj) and P’ (Non-Adj). • The next vertex will be chosen such that it has lexicographically largest label. • P’ is always located to the left most side of the Partitions List and will be processed first. • Any visited node will be removed from L=list. • LexBFS terminates since all vertices have been visited.
- 14. Conclusion • Choral Graph and its induced subgraphs admits a perfect elimination ordering. • Chordal graphes has vertex separators that separates the graph into distinct connected components by removal their. • LexBFS Algorithm is a polynomial algorithm that can give the answer of the identity of a graph is chordal or not. • There can be multiple perfect elimination ordering in a graph, Lex BFS can give multiple ordering as a part of start not. • However we need to know which percentage of perfect elimination orders can be observed by Lex BFS. • Still the labelling function of Lex BFS is not clear.
- 15. THANKS !