Limit fungsi dua peubah
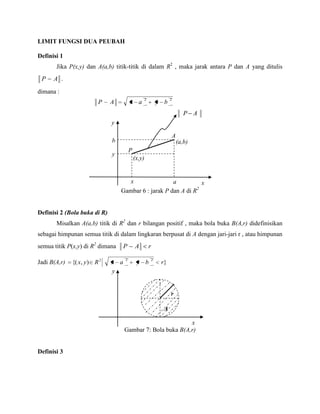
- 1. A x y (x,y) x y a b (a,b) P AP x y A r LIMIT FUNGSI DUA PEUBAH Definisi 1 Jika P(x,y) dan A(a,b) titik-titik di dalam R2 , maka jarak antara P dan A yang ditulis AP . dimana : 22 byaxAP Gambar 6 : jarak P dan A di R2 Definisi 2 (Bola buka di R) Misalkan A(a,b) titik di R2 dan r bilangan positif , maka bola buka B(A,r) didefinisikan sebagai himpunan semua titik di dalam lingkaran berpusat di A dengan jari-jari r , atau himpunan semua titik P(x,y) di R2 dimana rAP Jadi B(A,r) }),{( 222 rbyaxRyx Gambar 7: Bola buka B(A,r) Definisi 3
- 2. 0 B ,, 00 yxB L L L Z X Y Misalkan f fungsi dua peubah yang terdefinisi pada bola buka B(A,r) dan (x0,y0)titik limit dari B , maka Lyxfmil yxyx , 00 ,, jika 0 yang cukup kecil, maka terdapat 0 sehingga untuk setiap Byx, dan 2 0 2 0 yyxx berlaku Lyxf , Tafsiran geometris definisi limit fungsi dua peubah Dari gambar 8, jika (x,y) di dalam bola buka B(x0,y0, ), maka LyxfL , . Sifat : Jika lim f (x,y) = L1 dan lim g ( x ,y) = L2 (x,y ) (X0 ,Y0 ) (x,y) (x0 ,y0 ) Maka ï¶ lim f (x,y) + g ( x ,y)] = L1 + L2 (x,y ) (X0 ,Y0 ) ï¶ lim f (x,y) - g ( x ,y)] = L1 - L2 (x,y ) (X0 ,Y0 ) ï¶ lim f (x,y) . g ( x ,y)] = L1 . L2 (x,y ) (X0 ,Y0 ) ï¶ lim f (x,y) ] = k L1 , k = konstanta (x,y ) (X0 ,Y0 ) ï¶ lim = ,L2 â 0 (x,y ) (X0 ,Y0 ) Catatan:
- 3. Dalam konsep limit ini: 1. f tidak harus terdefinisi di (a,b). 2. Jika lim f (x,y) = L (x,y ) (a ,b ) ada maka bagaimanapun caranya (x,y) mendekati (a,b) nilai f(x,y) selalu mendekati L. Contoh 1 Buktikan 1132 3,1, yxmil yx Akan ditunjukkan bahwa untuk setiap 0, terdapat 0 sehingga 1132 yx , dimana 0 22 31 yx . Dengan menggunakan sifat baba diperoleh 331293221132 yxyxyx . Karena 22 311 yxx dan 22 313 yxy maka 33121132 yxyx 22 312 yx + 22 313 yx = 5315 22 yx , sebab 0 22 31 yx Dengan memilih 5 1 , maka 3233121132 yxyx dimana 0 22 31 yx Jadi terbukti bahwa
- 4. 1132 3,1, yxmil yx ( Diktat Matematika Dasar II Unhas ) Contoh Jika f ( x,y ) = maka lim f (x,y) tidak ada , buktikan ! (x,y ) (0 ,0 ) Penyelesaian : Titik (x, y) dapat mendekati (0,0) melalui tak hingga banyak arah.Untuk itu akan dilihat ketika (x, y) mendekati (0,0) sepanjang sumbu x, sumbu y. dan garis y = mx .Jika (x, y) mendekati (0,0) sepanjang(melalui) sumbu x ,jadi y = 0 , maka lim f (x,y) = lim (x,y ) (0 ,0) (x,y ) (0 ,0 ) = lim (x) (0) Di sisi lain, (x, y) mendekati (0,0) sepanjang(melalui) sumbu y (x = 0), maka lim f (x,y) = lim (x,y ) (0 ,0) (x,y ) (0 ,0 ) = lim (y) (0) = lim (y) (0)
- 5. Terlihat bahwa dari dua arah yang berbeda diperoleh nilai yang berbeda, dengan demikian dapat disimpulkan bahwa limit f tidak ada untuk (x, y) (0, 0). Pada contoh di atas kita tidak perlu mencari limit f dari arah lain, karena dari dua arah sudah didapatkan nilai yang berbeda, sehingga dapat segera disimpulkan bahwa limitnya tidak ada. Jika dari dua arah tersebut nilainya sama, perlu dicari dari arah lainnya, misal arah y = mx. KONTINUTAS Definisi 4 Fungsi f dua peubah dikatakan kontinu pada (x0,y0) jika memenuhi : i. f(x0,y0) ada ii. yxfmil yxyx , 00 ,, ada iii. 00 ,, ,, 00 yxfyxfmil yxyx Contoh 0 3 , 22 2 yx yx yxf Selidikilah kontinuitas di titik (0,0) Jawab : i. f(0,0) = 0 ada ii. yxfmil yx , 0,0, = 0 3 22 2 0,0, yx yx mil yx Bukti Jika (x, y) mendekati (0,0) sepanjang (melalui) sumbu x ,jadi y = 0 , maka *lim f (x,y) lim f (x,y) (x,y ) (0 ,0) (x , y ) (0 ,0) lim Jika (x,y) (0,0) Jika (x,y) = (0,0)
- 6. x 0 lim x 0 Jika (x, y) mendekati (0,0) sepanjang (melalui) sumbu y (x = 0), maka *lim f (x,y) lim f (x,y) (x,y ) (0 ,0) (x , y ) (0 ,0) lim y 0 lim y 0 Jika (x, y) mendekati (0,0) sepanjang(melalui) y = x , Maka; lim f (x,y) lim f (x,y) (x,y ) (0 ,0) (x , y ) (0 ,0) lim x 0 lim x 0 lim = lim = 0 x 0 Dapat disimpulkan bahwa lim f (x,y) = 0 (x,y ) (0 ,0)
- 7. iii. 00,0, 0,0, fyxfmil yx Jadi f(x,y) kontinu di titik (0,0). Contoh 2.7 0 , 22 yx xy yxf Selidikilah kontinuitas di titik (0,0) Jawab : i. f(0,0) = 0 ada ii. yxfmil yx , 0,0, = 22 0,0, yx xy mil yx Tidak ada limitnya Bukti Ambil S1 himpunan semua titik pada sumbu x berarti y = 0, maka yxfmil yx , 0,0, = 0, 0 xfmil x = 0 0 0 2 0 x mil x , 1, Syx Ambil S2 himpunan semua titik pada garis y = x maka yxfmil yx , 0,0, = 2 1 22 2 0 xx x mil x , 2, Syx karena yxfmil yx , 0,0, = 0 untuk (x,y) S1 tidak sama dengan yxfmil yx , 0,0, = 2 1 untuk (x,y) S2 berarti 22 0,0, yx xy mil yx tidak ada. Maka fungsi diatas tidak kontinu di titik ( 0,0 ) , jika (x,y) (0,0) , jika (x,y) = (0,0)
- 8. Tugas kelompok MATEMATIKA DASAR II âLIMIT DAN KEKONTINUANâ OLEH: KELOMPOK II JAMALUDDIN H22112011 AKMAL H22112268 MUH. IQBAL MAULANA H22112289 AHMAD JAMIL H12110290 UNIVERSITAS HASANUDDIN 2013

![0
B
,, 00 yxB
L
L
L
Z
X
Y
Misalkan f fungsi dua peubah yang terdefinisi pada bola buka B(A,r) dan (x0,y0)titik limit
dari B , maka
Lyxfmil
yxyx
,
00 ,,
jika 0 yang cukup kecil, maka terdapat 0 sehingga untuk setiap Byx, dan
2
0
2
0 yyxx berlaku Lyxf ,
Tafsiran geometris definisi limit fungsi dua peubah
Dari gambar 8, jika (x,y) di dalam bola buka B(x0,y0, ), maka LyxfL , .
Sifat :
Jika lim f (x,y) = L1 dan lim g ( x ,y) = L2
(x,y ) (X0 ,Y0 ) (x,y) (x0 ,y0 )
Maka
ï¶ lim f (x,y) + g ( x ,y)] = L1 + L2
(x,y ) (X0 ,Y0 )
ï¶ lim f (x,y) - g ( x ,y)] = L1 - L2
(x,y ) (X0 ,Y0 )
ï¶ lim f (x,y) . g ( x ,y)] = L1 . L2
(x,y ) (X0 ,Y0 )
ï¶ lim f (x,y) ] = k L1 , k = konstanta
(x,y ) (X0 ,Y0 )
ï¶ lim = ,L2 â 0
(x,y ) (X0 ,Y0 )
Catatan:](https://image.slidesharecdn.com/limitfungsiduapeubahtugas-130513002423-phpapp01/85/Limit-fungsi-dua-peubah-2-320.jpg)





