Linear regression vs polynomial regression v01
- 1. Linear Regression VS Polynomial Regression Ux?¨˘??
- 2. ˇďLinear Regression: The variable and the independent variable are linear, as with input and output, it is a linear relationship. [Step] Used the LinearRegression of sklearn.linear_model to construct the model. Used the fit method to fit the input data (X_train) and the output data (y_train) to construct a linear model Used the predict method to predict the results trained by this linear model. #1) Import linear regression from sklearn.linear_model import LinearRegression #2)Create a linear regression model LinearRegression_model = LinearRegression() #3) Train the model based on input and output data LinearRegression_model.fit(X_train, y_train) #4) Predicted value of training data y_pred = LinearRegression_model.predict(X_test)
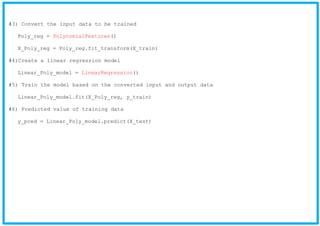
- 3. ˇďPolynomial Regression: It is an evolution based on linear regression. The independent variable will be transformed into n linear regressions, just as the input and output are not linear. When the polynomial power is larger, it means that the fit of the input and output is higher. However, this polynomial power is limited. If the polynomial power is too large, then predicted result will be diverged. [Step] Used the PolynomialFeatures of sklearn.preprocessing and fit_transform to transform the input data (X_train) Used the LinearRegression of sklearn.linear_model to construct the model. Used the fit method to fit the trnasform data (X_Poly_reg) and the output data (y_train) to construct a linear model Used the predict method to predict the results trained by this linear model. #1) Import linear regression from sklearn.linear_model import LinearRegression #2) Import polynomial regression from sklearn.preprocessing import PolynomialFeatures
- 4. #3) Convert the input data to be trained Poly_reg = PolynomialFeatures() X_Poly_reg = Poly_reg.fit_transform(X_train) #4)Create a linear regression model Linear_Poly_model = LinearRegression() #5) Train the model based on the converted input and output data Linear_Poly_model.fit(X_Poly_reg, y_train) #6) Predicted value of training data y_pred = Linear_Poly_model.predict(X_test)
- 5. ˇďAssuming the annual salary corresponding to the seniority of the university from the assistant to the professor (the following data is for reference only).
- 6. The Assistant is divided into Assistant-1 and Assistant-2. Assistant-1 is the annual salary of 300,000 NT for the 1st year of assistant Assistant-2 is the annual salary of 400,000 NT for the 2nd year of assistant The Lecturer is divided into Lecturer-1, Lecturer-2 and Lecturer-3. Lecturer-1 is the annual salary of 600,000 NT for the 1st year of Lecturer Lecturer-2 is the annual salary of 700,000 NT for the 2nd year of Lecturer Lecturer-3 is the annual salary of 800,000 NT for the 3rd year of Lecturer The Assistant Professor is divided into Assistant Professor-1, Assistant Professor-2 and Assistant Professor-3. Assistant Professor-1 is the annual salary of 1,000,000 NT for the 1st year of Assistant Professor Assistant Professor-2 is the annual salary of 1,100,000 NT for the 2nd year of Assistant Professor Assistant Professor-3 is the annual salary of 1,200,000 NT for the 3rd year of Assistant Professor
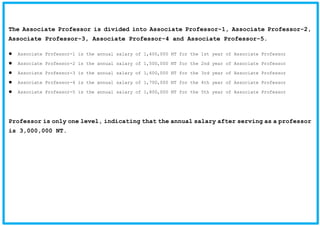
- 7. The Associate Professor is divided into Associate Professor-1, Associate Professor-2, Associate Professor-3, Associate Professor-4 and Associate Professor-5. Associate Professor-1 is the annual salary of 1,400,000 NT for the 1st year of Associate Professor Associate Professor-2 is the annual salary of 1,500,000 NT for the 2nd year of Associate Professor Associate Professor-3 is the annual salary of 1,600,000 NT for the 3rd year of Associate Professor Associate Professor-4 is the annual salary of 1,700,000 NT for the 4th year of Associate Professor Associate Professor-5 is the annual salary of 1,800,000 NT for the 5th year of Associate Professor Professor is only one level, indicating that the annual salary after serving as a professor is 3,000,000 NT.
- 8. Frank, Peter, John learned that a university is hiring lecturers, assistant professors, and associate professors. Frank is a lecturer with 1 year of experience, and total seniority is 4.5 years. He expects an annual salary of 660,000 NT. Peter is an assistant professor with 1 year of experience, and total seniority is 7.5 years. He expects an annual salary of 1,480,000 NT. John is an associate professor with 5 year of experience, and total seniority is 14.5 years. He expects an annual salary of 2,000,000 NT. Calculate the estimated annual salary of 3 people through linear regression and polynomial regression.
- 9. ˇď[Linear regression - estimated results] Frank: Below the expected annual salary Estimated 650,310 NT Expectation 660,000 NT Peter: Below the expected annual salary Estimated 1,094,513 NT Expectation 1,480,000 NT John: Higher than expected annual salary Eestimated 2,130,987 NT Expected 2,000,000 NT Conclusion: Using linear regression estimates, only John is above the expected annual salary, while Frank and Peter are below the expected annual salary.
- 10. ˇď[Polynomial (2 times) regression - estimated results] Frank: Below the expected annual salary Estimated 606,343 NT Expectation 660,000 NT Peter: Below the expected annual salary Estimated 950,450 NT Expected 1,480,000 NT John: Higher than expected annual salary Estimated 2,318,336 NT Expected 2,000,000 NT Conclusion: Using polynomial (2) regression estimates, only John is above the expected annual salary, while Frank and Peter are below the expected annual salary.
- 11. ˇď[Polynomial (3 times) regression - estimated results] Frank: Higher than expected annual salary Estimated 745,445 NT Expected 660,000 NT Peter: Below the expected annual salary Estimated 983,399 NT Expectation 1,480,000 NT John: Higher than expected annual salary Estimated 2,417,164 NT Expected 2,000,000 NT Conclusion: Using polynomial (3) regression estimates, Frank and John are higher than expected annual salary, and Peter is lower than expected annual salary.
- 12. ˇď[Polynomial (4 times) regression - estimated results] Frank: Below the expected annual salary Estimated 617,459 NT Expectation 660,000 NT Peter: Below the expected annual salary Estimated 1,106,490 NT Expectation 1,480,000 NT John: Higher than expected annual salary Estimated 2,436,659 NT Expected 2,000,000 NT Conclusion: Using polynomial (4th) regression estimates, only John is above the expected annual salary, while Frank and Peter are lower than expected annual salary.
- 13. ˇď[Polynomial (5 times) regression - estimated results] Frank: Below the expected annual salary Estimated 609,801 NT Expectation 660,000 NT Peter: Below the expected annual salary Estimated 1,057,121 NT Expectation 1,480,000 NT John: Higher than expected annual salary Estimated 2,380,753 NT Expected 2,000,000 NT Conclusion: Using polynomial (5th) regression estimates, only John is above the expected annual salary, while Frank and Peter are lower than expected annual salary.
- 14. ˇď[Polynomial (6 times) regression - estimated results] Frank: Below the expected annual salary Estimated 681,618 NT Expectation 660,000 NT Peter: Below the expected annual salary Estimated 993,186 NT Expectation 1,480,000 NT John: Higher than expected annual salary Estimated 2,301,332 NT Expected 2,000,000 NT Conclusion: Using polynomial (6 times) regression estimates, Frank and John are higher than expected annual salary, and Peter is lower than expected annual salary.
- 15. ˇď[Polynomial (7 times) regression - estimated results] Frank: Below the expected annual salary Estimated 637,321 NT Expectation 660,000 NT Peter: Below the expected annual salary Estimated 1,021,298 NT Expectation 1,480,000 NT John: Higher than expected annual salary Estimated 2,219,468 NT Expected 2,000,000 NT Conclusion: Using the polynomial (7) regression estimates, only John is above the expected annual salary, while Frank and Peter are below the expected annual salary.
- 16. ˇď[Polynomial (8 times) regression - estimated results] Frank: Below the expected annual salary Estimated 641,562 NT Expectation 660,000 NT Peter: Below the expected annual salary Estimated 1,042,994 NT Expectation 1,480,000 NT John: Higher than expected annual salary Estimated 2,156,521 NT Expected 2,000,000 NT Conclusion: Using polynomial (8th) regression estimates, only John is above the expected annual salary, while Frank and Peter are lower than expected annual salary.
- 17. ˇď[Polynomial (9 times) regression - estimated results] Frank: Below the expected annual salary Estimated 645088 NT Expectation 660,000 NT Peter: Below the expected annual salary Estimated 1,037,883 NT Expectation 1,480,000 NT John: Higher than expected annual salary Estimated 2,140,541 NT Expected 2,000,000 NT Conclusion: Using polynomial (9th) regression estimates, only John is above the expected annual salary, while Frank and Peter are below the expected annual salary.
- 18. ˇď[Polynomial (10 times) regression - estimated results] Frank: Below the expected annual salary Estimated 625,914 NT Expectation 660,000 NT Peter: Below the expected annual salary Estimated 1,034,544 NT Expectation 1,480,000 NT John: Higher than expected annual salary Estimated 2,071,768 NT Expected 2,000,000 NT Conclusion: Using the polynomial (10) regression estimates, only John is above the expected annual salary, while Frank and Peter are below the expected annual salary.
- 19. ˇďPolynomial (20 times) regression - estimated results] Frank: Below the expected annual salary Estimated 511,808 NT Expectation 660,000 NT Peter: Below the expected annual salary Estimated 1,104,684 NT Expectation 1,480,000 NT John: Higher than expected annual salary Estimated 14,151,479 NT Expected 2,000,000 NT Conclusion: Using polynomial (20) regression estimates, only John is above the expected annual salary, while Frank and Peter are below the expected annual salary.
- 20. ˇďPolynomial (30 times) regression - estimated results] Frank: Higher the expected annual salary Estimated 708,252 NT Expectation 660,000 NT Peter: Below the expected annual salary Estimated 724,531 NT Expectation 1,480,000 NT John: Higher than expected annual salary Estimated 145,217,400 NT Expected 2,000,000 NT Conclusion: Using polynomial (30) regression estimates, Frank and John are higher than expected annual salary, and Peter is lower than expected annual salary.
- 21. ˇďPolynomial (100 times) regression - estimated results] Frank: Higher the expected annual salary Estimated 900,060 NT Expectation 660,000 NT Peter: Below the expected annual salary Estimated 900,060 NT Expectation 1,480,000 NT John: Higher than expected annual salary Estimated 4,078,739,520,000 NT Expected 2,000,000 NT Conclusion: Using polynomial (100 times) regression estimates, Frank and John are higher than expected annual salary, and Peter is lower than expected annual salary.
- 22. ˇďConclusion 1. When the input and output data have approximate slopes, linear regression can be used to predict the result, but the accuracy is still insufficient. 2. Using linear regression to polynomial regression (2 to 10 times), comparing the estimated annual salary with the expected annual salary of 3 people, Frank's expected annual salary may be higher than the estimated annual salary. John's expected annual salary is completely lower than the estimated annual salary. Peter's expected annual salary is higher than the estimated annual salary, so Peter need to adjust the expected annual salary to meet market demand.
- 23. 3. From the simulation results of polynomial regression, the fit of 7 to 10 times are very high, so we can refer to the estimated annual salary using these multiple regressions. 4. From the simulation results of polynomial regression (20 times), it is estimated that the annual salary of the previous paragraph has deviated somewhat, even to the polynomial regression (100 times). Most of the estimated annual salary deviates from the original data. The annual salary is also completely distorted and cannot be referenced, so the function of too high a number of times causes over-fitting, so that the predicted result is divergent.

![ˇďLinear Regression:
The variable and the independent variable are linear, as with input and output, it is a linear
relationship.
[Step]
Used the LinearRegression of sklearn.linear_model to construct the model.
Used the fit method to fit the input data (X_train) and the output data (y_train) to construct
a linear model
Used the predict method to predict the results trained by this linear model.
#1) Import linear regression
from sklearn.linear_model import LinearRegression
#2)Create a linear regression model
LinearRegression_model = LinearRegression()
#3) Train the model based on input and output data
LinearRegression_model.fit(X_train, y_train)
#4) Predicted value of training data
y_pred = LinearRegression_model.predict(X_test)](https://image.slidesharecdn.com/linearregressionvspolynomialregressionv01-190403091851/85/Linear-regression-vs-polynomial-regression-v01-2-320.jpg)
![ˇďPolynomial Regression:
It is an evolution based on linear regression. The independent variable will be transformed into
n linear regressions, just as the input and output are not linear.
When the polynomial power is larger, it means that the fit of the input and output is higher.
However, this polynomial power is limited. If the polynomial power is too large, then predicted
result will be diverged.
[Step]
Used the PolynomialFeatures of sklearn.preprocessing and fit_transform to transform the input
data (X_train)
Used the LinearRegression of sklearn.linear_model to construct the model.
Used the fit method to fit the trnasform data (X_Poly_reg) and the output data (y_train) to construct
a linear model
Used the predict method to predict the results trained by this linear model.
#1) Import linear regression
from sklearn.linear_model import LinearRegression
#2) Import polynomial regression
from sklearn.preprocessing import PolynomialFeatures](https://image.slidesharecdn.com/linearregressionvspolynomialregressionv01-190403091851/85/Linear-regression-vs-polynomial-regression-v01-3-320.jpg)



![ˇď[Linear regression - estimated results]
Frank: Below the expected annual salary
Estimated 650,310 NT
Expectation 660,000 NT
Peter: Below the expected annual salary
Estimated 1,094,513 NT
Expectation 1,480,000 NT
John: Higher than expected annual salary
Eestimated 2,130,987 NT
Expected 2,000,000 NT
Conclusion: Using linear regression estimates, only John is above the expected annual salary, while
Frank and Peter are below the expected annual salary.](https://image.slidesharecdn.com/linearregressionvspolynomialregressionv01-190403091851/85/Linear-regression-vs-polynomial-regression-v01-9-320.jpg)
![ˇď[Polynomial (2 times) regression - estimated results]
Frank: Below the expected annual salary
Estimated 606,343 NT
Expectation 660,000 NT
Peter: Below the expected annual salary
Estimated 950,450 NT
Expected 1,480,000 NT
John: Higher than expected annual salary
Estimated 2,318,336 NT
Expected 2,000,000 NT
Conclusion: Using polynomial (2) regression estimates, only John is above the expected annual salary,
while Frank and Peter are below the expected annual salary.](https://image.slidesharecdn.com/linearregressionvspolynomialregressionv01-190403091851/85/Linear-regression-vs-polynomial-regression-v01-10-320.jpg)
![ˇď[Polynomial (3 times) regression - estimated results]
Frank: Higher than expected annual salary
Estimated 745,445 NT
Expected 660,000 NT
Peter: Below the expected annual salary
Estimated 983,399 NT
Expectation 1,480,000 NT
John: Higher than expected annual salary
Estimated 2,417,164 NT
Expected 2,000,000 NT
Conclusion: Using polynomial (3) regression estimates, Frank and John are higher than expected annual
salary, and Peter is lower than expected annual salary.](https://image.slidesharecdn.com/linearregressionvspolynomialregressionv01-190403091851/85/Linear-regression-vs-polynomial-regression-v01-11-320.jpg)
![ˇď[Polynomial (4 times) regression - estimated results]
Frank: Below the expected annual salary
Estimated 617,459 NT
Expectation 660,000 NT
Peter: Below the expected annual salary
Estimated 1,106,490 NT
Expectation 1,480,000 NT
John: Higher than expected annual salary
Estimated 2,436,659 NT
Expected 2,000,000 NT
Conclusion: Using polynomial (4th) regression estimates, only John is above the expected annual
salary, while Frank and Peter are lower than expected annual salary.](https://image.slidesharecdn.com/linearregressionvspolynomialregressionv01-190403091851/85/Linear-regression-vs-polynomial-regression-v01-12-320.jpg)
![ˇď[Polynomial (5 times) regression - estimated results]
Frank: Below the expected annual salary
Estimated 609,801 NT
Expectation 660,000 NT
Peter: Below the expected annual salary
Estimated 1,057,121 NT
Expectation 1,480,000 NT
John: Higher than expected annual salary
Estimated 2,380,753 NT
Expected 2,000,000 NT
Conclusion: Using polynomial (5th) regression estimates, only John is above the expected annual
salary, while Frank and Peter are lower than expected annual salary.](https://image.slidesharecdn.com/linearregressionvspolynomialregressionv01-190403091851/85/Linear-regression-vs-polynomial-regression-v01-13-320.jpg)
![ˇď[Polynomial (6 times) regression - estimated results]
Frank: Below the expected annual salary
Estimated 681,618 NT
Expectation 660,000 NT
Peter: Below the expected annual salary
Estimated 993,186 NT
Expectation 1,480,000 NT
John: Higher than expected annual salary
Estimated 2,301,332 NT
Expected 2,000,000 NT
Conclusion: Using polynomial (6 times) regression estimates, Frank and John are higher than expected
annual salary, and Peter is lower than expected annual salary.](https://image.slidesharecdn.com/linearregressionvspolynomialregressionv01-190403091851/85/Linear-regression-vs-polynomial-regression-v01-14-320.jpg)
![ˇď[Polynomial (7 times) regression - estimated results]
Frank: Below the expected annual salary
Estimated 637,321 NT
Expectation 660,000 NT
Peter: Below the expected annual salary
Estimated 1,021,298 NT
Expectation 1,480,000 NT
John: Higher than expected annual salary
Estimated 2,219,468 NT
Expected 2,000,000 NT
Conclusion: Using the polynomial (7) regression estimates, only John is above the expected annual
salary, while Frank and Peter are below the expected annual salary.](https://image.slidesharecdn.com/linearregressionvspolynomialregressionv01-190403091851/85/Linear-regression-vs-polynomial-regression-v01-15-320.jpg)
![ˇď[Polynomial (8 times) regression - estimated results]
Frank: Below the expected annual salary
Estimated 641,562 NT
Expectation 660,000 NT
Peter: Below the expected annual salary
Estimated 1,042,994 NT
Expectation 1,480,000 NT
John: Higher than expected annual salary
Estimated 2,156,521 NT
Expected 2,000,000 NT
Conclusion: Using polynomial (8th) regression estimates, only John is above the expected annual
salary, while Frank and Peter are lower than expected annual salary.](https://image.slidesharecdn.com/linearregressionvspolynomialregressionv01-190403091851/85/Linear-regression-vs-polynomial-regression-v01-16-320.jpg)
![ˇď[Polynomial (9 times) regression - estimated results]
Frank: Below the expected annual salary
Estimated 645088 NT
Expectation 660,000 NT
Peter: Below the expected annual salary
Estimated 1,037,883 NT
Expectation 1,480,000 NT
John: Higher than expected annual salary
Estimated 2,140,541 NT
Expected 2,000,000 NT
Conclusion: Using polynomial (9th) regression estimates, only John is above the expected annual
salary, while Frank and Peter are below the expected annual salary.](https://image.slidesharecdn.com/linearregressionvspolynomialregressionv01-190403091851/85/Linear-regression-vs-polynomial-regression-v01-17-320.jpg)
![ˇď[Polynomial (10 times) regression - estimated results]
Frank: Below the expected annual salary
Estimated 625,914 NT
Expectation 660,000 NT
Peter: Below the expected annual salary
Estimated 1,034,544 NT
Expectation 1,480,000 NT
John: Higher than expected annual salary
Estimated 2,071,768 NT
Expected 2,000,000 NT
Conclusion: Using the polynomial (10) regression estimates, only John is above the expected annual
salary, while Frank and Peter are below the expected annual salary.](https://image.slidesharecdn.com/linearregressionvspolynomialregressionv01-190403091851/85/Linear-regression-vs-polynomial-regression-v01-18-320.jpg)
![ˇďPolynomial (20 times) regression - estimated results]
Frank: Below the expected annual salary
Estimated 511,808 NT
Expectation 660,000 NT
Peter: Below the expected annual salary
Estimated 1,104,684 NT
Expectation 1,480,000 NT
John: Higher than expected annual salary
Estimated 14,151,479 NT
Expected 2,000,000 NT
Conclusion: Using polynomial (20) regression estimates, only John is above the expected annual salary,
while Frank and Peter are below the expected annual salary.](https://image.slidesharecdn.com/linearregressionvspolynomialregressionv01-190403091851/85/Linear-regression-vs-polynomial-regression-v01-19-320.jpg)
![ˇďPolynomial (30 times) regression - estimated results]
Frank: Higher the expected annual salary
Estimated 708,252 NT
Expectation 660,000 NT
Peter: Below the expected annual salary
Estimated 724,531 NT
Expectation 1,480,000 NT
John: Higher than expected annual salary
Estimated 145,217,400 NT
Expected 2,000,000 NT
Conclusion: Using polynomial (30) regression estimates, Frank and John are higher than expected
annual salary, and Peter is lower than expected annual salary.](https://image.slidesharecdn.com/linearregressionvspolynomialregressionv01-190403091851/85/Linear-regression-vs-polynomial-regression-v01-20-320.jpg)
![ˇďPolynomial (100 times) regression - estimated results]
Frank: Higher the expected annual salary
Estimated 900,060 NT
Expectation 660,000 NT
Peter: Below the expected annual salary
Estimated 900,060 NT
Expectation 1,480,000 NT
John: Higher than expected annual salary
Estimated 4,078,739,520,000 NT
Expected 2,000,000 NT
Conclusion: Using polynomial (100 times) regression estimates, Frank and John are higher than expected
annual salary, and Peter is lower than expected annual salary.](https://image.slidesharecdn.com/linearregressionvspolynomialregressionv01-190403091851/85/Linear-regression-vs-polynomial-regression-v01-21-320.jpg)

