�ݺ�ߣ

LINEAR TRANSFORMATION
Dr A K Tiwari Director TI Jabalpur ashokktiwari@gmail.com

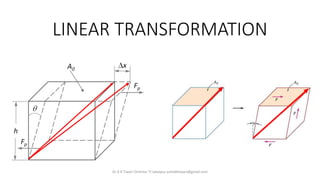
• A linear equation is an equation that has one or more variables
having degree one.
• Matrix multiplication method and gaussian elimination method are
two methods to solve linear equations using matrices.
Ax=b

Representing a linear system with matrices
A system of equations can be represented by an augmented matrix.
In an augmented matrix, each row represents one equation in the system and each column represents
a variable or the constant terms.
In this way, we can see that augmented matrices are a shorthand way of writing systems of equations.
The organization of the numbers into the matrix makes it unnecessary to write various symbols like x, y,
z and =equals , yet all of the information is still there!

Which system is represented by the augmented
matrix?

LINEAR SYSTEM
• principle of superposition
• Homogeneity: A system is said to be homogeneous, if we multiply input
with some constant A then the output will also be multiplied by the same
value of constant (i.e. A).
• Additivity: Suppose we have a system S and we are giving the input to this
system as a1 for the first time and we are getting the output as b1
corresponding to input a1. On the second time we are giving input a2 and
correspond to this we are getting the output as b2.
• Now suppose this time we are giving input as a summation of the previous
inputs (i.e. a1 + a2) and corresponding to this input suppose we are getting
the output as (b1 + b2) then we can say that system S is following the
property of additivity.
S

1.A matrix is a rectangular array of numbers while a vector is a mathematical quantity that
has magnitude and direction.
2.A vector and a matrix are both represented by a letter with a vector typed in boldface with
an arrow above it to distinguish it from real numbers while a matrix is typed in an upper-
case letter.
3.Vectors are used in geometry to simplify certain 3D problems while matrices are key tools
used in linear algebra.
4.A vector is an array of numbers with a single index while a matrix is an array of numbers
with two indices.
5.While a vector is used to represent magnitude and direction, a matrix is used to represent
linear transformations and keep track of coefficients in linear equations.
P = xi + yj + zk.

Vectors are a collection of components which are
related to a set of basis vectors
basis vectors x^ and y^ for the basis vectors along
the x−axis and y−axis respectively.
vectors as points in space, assuming the tail is always at
the origin and the head is at the specified point.
Vector as column matrices

THIS MATRIX HAS 3 VECTORS

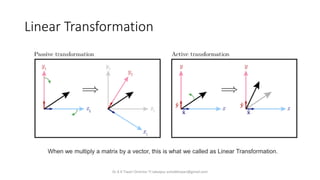
Linear Transformation
When we multiply a matrix by a vector, this is what we called as Linear Transformation.

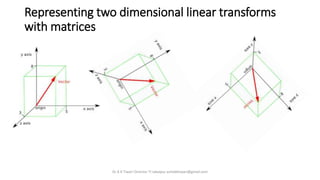
Representing two dimensional linear transforms
with matrices

Representing three dimensional linear transforms with matrices

(eigen- meaning own, belonging to oneself, in
German)
• The eigenvectors are the directions in which the matrix acts solely as a scaling transformation, and
the eigenvalues are the corresponding scale factors.
• eigenvectors of a matrix are those direction in the space that after the matrix operating on them,
they supply the same direction with some coefficient of proportionality between "old" and "new"
direction that are eigenvalues.
• The eigen functions represent stationary states of the system i.e. the system can achieve that state
under certain conditions and eigenvalues represent the value of that property of the system in that
stationary state.
• the eigenvectors are the special directions where the linear operator A simply acts through scaling.
• Each Eigenvalue has a set of eigenvectors.
• Eigenvalues and eigenvectors are linearly dependent

Eigenvalue =2 , eigenvector P = 2
2
Same direction
EXPAND 2 times

�ݺ�ߣ

LINEAR TRANSFORMATION22.pptx

More Related Content

LINEAR TRANSFORMATION22.pptx