Beats
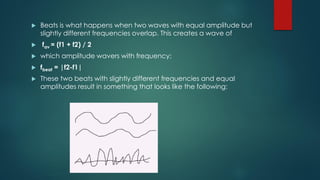
- 2.  Beats is what happens when two waves with equal amplitude but slightly different frequencies overlap. This creates a wave of  fav = (f1 + f2) / 2  which amplitude wavers with frequency:  fbeat = |f2-f1|  These two beats with slightly different frequencies and equal amplitudes result in something that looks like the following:
- 3.  A great example that demonstrates this is when you are tuning a piano with a tuning fork. When you listen to the tuning fork and the piano string is close to the tuning fork, you start to hear some weird vibrations. As the string and tuning fork get closer together, the beat gets longer and longer, eventually to the point where you hear nothing.
- 4. Question  Cindy has 2 tuning forks. One with a frequency of 320 Hz and the other tuning fork with an unknown frequency. Cindy hears 7 beats in 3.5 seconds. What is the frequency of the unknown tuning fork.
- 5. Solution  Beat Frequency is cycles over time so since Cindy hears 7 beats in 3.5 seconds, we get 7/3.5 = 2 Hz  Using the equation: fbeat = |f2-f1|, we can isolate f2 since we know the frequency of the beat and the frequency of the first tuning fork. Getting rid of the absolute value changes the fbeat to either positive or negative, so we now have two cases, a positive and a negative beat. +2 = f2 – 320 and -2 = f2 – 320 f2 = 318 Hz or 322 Hz. If the second tuning fork sounded lower than the first tuning fork than it would have a frequency of 318 Hz while if it sounded higher than the first tuning fork then it would have a frequency of 322