Logarithmic function, equation and inequality
- 1. LOGARITHMIC FUNCTION, LOGARITHMIC EQUATION AND LOGARITHMIC INEQUALITY ’ü« FELINA E. VICTORIA ’ü« MAED-MATH
- 2. ’ü«
- 3. Example 1: Solution: log2 8 ’ĆĮ 3 We read this as: ŌĆØthe log base 2 of 8 is equal to 3ŌĆØ. 3 Write 2 8 in logarithmic form.’ĆĮ
- 4. Example 1a: Write 42 ’ĆĮ16 in logarithmic form. Solution: log4 16 ’ĆĮ 2 Read as: ŌĆ£the log base 4 of 16 is equal to 2ŌĆØ.
- 5. Example 1b: Solution: Write 2 ’ĆŁ 3 ’ĆĮ 1 8 in logarithmic form. log2 1 8 ’ĆĮ ’ĆŁ 3 1 Read as: "the log base 2 of is equal to -3". 8
- 6. Okay, so now itŌĆÖs time for you to try some on your own. 1. Write 72 ’ĆĮ 49 in logarithmic form. 7Solution: log 49 2’ĆĮ
- 7. log5 1’ĆĮ 0Solution: 2. Write 50 ’ĆĮ 1 in logarithmic form.
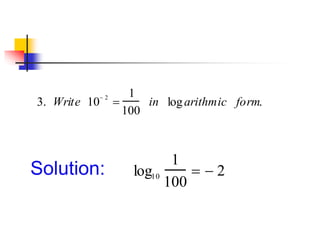
- 8. 3. Write 10 ’ĆŁ 2 ’ĆĮ 1 100 in logarithmic form. Solution: log10 1 100 ’ĆĮ ’ĆŁ 2
- 9. Solution: log16 4 ’ĆĮ 1 2 4. Finally, write 16 1 2 ’ĆĮ 4 in logarithmic form.
- 10. Example 1: Write log3 81’ĆĮ 4 in exp onential form Solution: 34 ’ĆĮ 81
- 11. Example 2: Write log2 1 8 ’ĆĮ ’ĆŁ 3 in exp onential form. Solution: 2 ’ĆŁ 3 ’ĆĮ 1 8
- 12. Okay, now you try these next three. 1. Write log10 100 ’ĆĮ 2 in exp onential form. 3. Write log27 3 ’ĆĮ 1 3 in exp onential form. 2. Write log5 1 125 ’ĆĮ ’ĆŁ 3 in exp onential form.
- 13. 1. Write log10 100 ’ĆĮ 2 in exp onential form. Solution: 102 ’ĆĮ100
- 14. 2. Write log5 1 125 ’ĆĮ ’ĆŁ 3 in exp onential form. Solution: 3 1 5 125 ’ĆŁ ’ĆĮ
- 15. 3. Write log27 3 ’ĆĮ 1 3 in exp onential form. Solution: 27 1 3 ’ĆĮ 3
- 16. Solution: LetŌĆÖs rewrite the problem in exponential form. 62 ’ĆĮ x WeŌĆÖre finished ! 6Solve for x: log 2x ’ĆĮ Example 1
- 17. Solution: 5 y ’ĆĮ 1 25 Rewrite the problem in exponential form. Since 1 25 ’ĆĮ 5’ĆŁ 2’ā”’ĆĀ ’ā©’ĆĀ ’ā¦’ĆĀ ’āČ’ĆĀ ’āĖ’ĆĀ ’āĘ’ĆĀ 5y ’ĆĮ 5’ĆŁ 2 y ’ĆĮ ’ĆŁ2 5 1 Solve for y: log 25 y’ĆĮ Example 2
- 18. Example 3 Evaluate log3 27. Try setting this up like this: Solution: log3 27 ’ĆĮ y Now rewrite in exponential form. 3y ’ĆĮ 27 3y ’ĆĮ 33 y ’ĆĮ 3
- 19. These next two problems tend to be some of the trickiest to evaluate. Actually, they are merely identities and the use of our simple rule will show this.
- 20. Example 4 Evaluate: log7 72 Solution: Now take it out of the logarithmic form and write it in exponential form. log7 72 ’ĆĮ y First, we write the problem with a variable. 7y ’ĆĮ 72 y ’ĆĮ 2
- 21. Example 5 Evaluate: 4log 4 16 Solution: 4 log 4 16 ’ĆĮ y First, we write the problem with a variable. log4 y ’ĆĮ log4 16 Now take it out of the exponential form and write it in logarithmic form. Just like 23 ’ĆĮ 8 converts to log2 8 ’ĆĮ 3 y ’ĆĮ 16
- 22. Example 1 Solve: log3 (4x ’Ć½10) ’ĆĮ log3 (x ’Ć½1) Solution: Since the bases are both ŌĆś3ŌĆÖ we simply set the arguments equal. 4x’Ć½10’ĆĮ x’Ć½1 3x’Ć½10’ĆĮ1 3x ’ĆĮ ’ĆŁ 9 x ’ĆĮ ’ĆŁ 3
- 23. Example 2 Solve: log8 (x2 ’ĆŁ14) ’ĆĮ log8 (5x) Solution: Since the bases are both ŌĆś8ŌĆÖ we simply set the arguments equal. x2 ’ĆŁ14 ’ĆĮ 5x x2 ’ĆŁ 5x ’ĆŁ14 ’ĆĮ 0 (x ’ĆŁ 7)(x ’Ć½ 2)’ĆĮ 0 Factor (x ’ĆŁ 7)’ĆĮ 0 or (x ’Ć½ 2)’ĆĮ 0 x ’ĆĮ 7 or x ’ĆĮ ’ĆŁ2 continued on the next page