Logic gates ppt
- 1. Boolean Algebra Logic Gates 4/30/2018 Pavithran Puthiyapurayil , Maldives National University 1
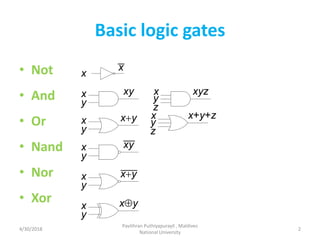
- 2. 2 Basic logic gates • Not • And • Or • Nand • Nor • Xor x x x y xy x y xyz z x+yx y x y x+y+z z x y xy x+yx y xÅyx y 4/30/2018 Pavithran Puthiyapurayil , Maldives National University
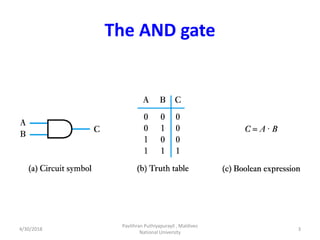
- 3. The AND gate 4/30/2018 Pavithran Puthiyapurayil , Maldives National University 3
- 4. The OR gate 4/30/2018 Pavithran Puthiyapurayil , Maldives National University 4
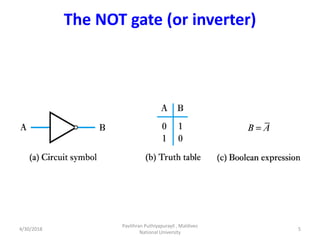
- 5. The NOT gate (or inverter) 4/30/2018 Pavithran Puthiyapurayil , Maldives National University 5
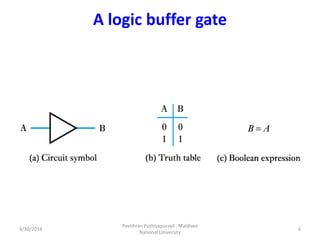
- 6. A logic buffer gate 4/30/2018 Pavithran Puthiyapurayil , Maldives National University 6
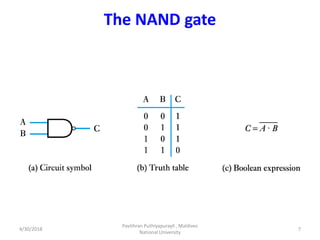
- 7. The NAND gate 4/30/2018 Pavithran Puthiyapurayil , Maldives National University 7
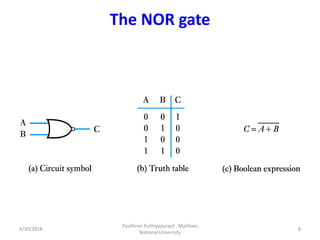
- 8. The NOR gate 4/30/2018 Pavithran Puthiyapurayil , Maldives National University 8
- 9. The Exclusive OR gate 4/30/2018 Pavithran Puthiyapurayil , Maldives National University 9
- 10. The Exclusive NOR gate 4/30/2018 Pavithran Puthiyapurayil , Maldives National University 10
- 11. Boolean Algebra • Boolean Constants – these are ‘0’ (false) and ‘1’ (true) • Boolean Variables – variables that can only take the vales ‘0’ or ‘1’ • Boolean Functions – each of the logic functions (such as AND, OR and NOT) are represented by symbols as described above • Boolean Theorems – a set of identities and laws – see text for details 4/30/2018 Pavithran Puthiyapurayil , Maldives National University 11
- 12. Boolean laws ABBA BAAB ++  ))(( )( CABABCA BCABCBA +++ ++ CBACBA CABBCA ++++  )()( )()( ABAA AABA + + )( BABA BABA + + ABBAA BABAA + ++ )( 4/30/2018 Pavithran Puthiyapurayil , Maldives National University 12
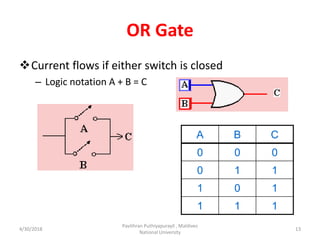
- 13. OR Gate Current flows if either switch is closed – Logic notation A + B = C A B C 0 0 0 0 1 1 1 0 1 1 1 1 4/30/2018 Pavithran Puthiyapurayil , Maldives National University 13
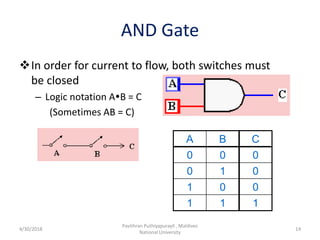
- 14. AND Gate In order for current to flow, both switches must be closed – Logic notation AB = C (Sometimes AB = C) A B C 0 0 0 0 1 0 1 0 0 1 1 1 4/30/2018 Pavithran Puthiyapurayil , Maldives National University 14
- 15. Properties of AND and OR • Commutation o A + B = B + A o A  B = B  A Same as Same as 4/30/2018 Pavithran Puthiyapurayil , Maldives National University 15
- 16. Commutation Circuit A + B B + A A ÔÇü B B ÔÇü A 4/30/2018 Pavithran Puthiyapurayil , Maldives National University 16
- 17. Properties of AND and OR • Associative Property A + (B + C) = (A + B) + C A  (B  C) = (A  B)  C = 4/30/2018 Pavithran Puthiyapurayil , Maldives National University 17
- 18. Distributive Property (A + B) ÔÇü (A + C) A B C Q 0 0 0 0 0 0 1 0 0 1 0 0 0 1 1 1 1 0 0 1 1 0 1 1 1 1 0 1 1 1 1 1 4/30/2018 Pavithran Puthiyapurayil , Maldives National University 18
- 19. Binary Addition A B S C(arry) 0 0 0 0 1 0 1 0 0 1 1 0 1 1 0 1 Notice that the carry results are the same as AND C = A ÔÇü B 4/30/2018 Pavithran Puthiyapurayil , Maldives National University 19
- 20. Inversion (NOT) A Q 0 1 1 0 Logic: AQ ÔÄΩ 4/30/2018 Pavithran Puthiyapurayil , Maldives National University 20
- 21. Circuit for XOR Accumulating our results: Binary addition is the result of XOR plus AND BABABA ÔÉó+ÔÉóÔÄΩ√Ö 4/30/2018 Pavithran Puthiyapurayil , Maldives National University 21
- 22. 22 Converting between circuits and equations • Find the output of the following circuit • Answer: (x+y)y – Or (xy)y x y x+y y (x+y)y __ x y y 4/30/2018 Pavithran Puthiyapurayil , Maldives National University
- 23. 23 x y Converting between circuits and equations • Find the output of the following circuit • Answer: xy – Or (xy) ≡ xy x y x y x y _ ____ 4/30/2018 Pavithran Puthiyapurayil , Maldives National University
- 24. 24 Converting between circuits and equations • Write the circuits for the following Boolean algebraic expressions a) x+y x y x y x y __ x x+y 4/30/2018 Pavithran Puthiyapurayil , Maldives National University
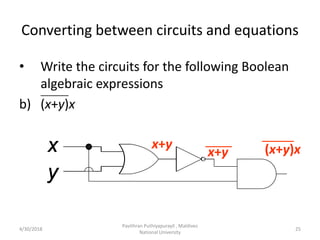
- 25. 25 x y x y x y Converting between circuits and equations • Write the circuits for the following Boolean algebraic expressions b) (x+y)x _______ x y x+y x+y (x+y)x 4/30/2018 Pavithran Puthiyapurayil , Maldives National University
- 26. 26 Writing xor using and/or/not • p Å q  (p  q)  ¬(p  q) • x Å y  (x + y)(xy) x y xÅy 1 1 0 1 0 1 0 1 1 0 0 0 x y x+y xy xy (x+y)(xy) ____ 4/30/2018 Pavithran Puthiyapurayil , Maldives National University
- 27. 27 Converting decimal numbers to binary • 53 = 32 + 16 + 4 + 1 = 25 + 24 + 22 + 20 = 1*25 + 1*24 + 0*23 + 1*22 + 0*21 + 1*20 = 110101 in binary = 00110101 as a full byte in binary • 211= 128 + 64 + 16 + 2 + 1 = 27 + 26 + 24 + 21 + 20 = 1*27 + 1*26 + 0*25 + 1*24 + 0*23 + 0*22 + 1*21 + 1*20 = 11010011 in binary 4/30/2018 Pavithran Puthiyapurayil , Maldives National University
- 28. 28 Converting binary numbers to decimal • What is 10011010 in decimal? 10011010 = 1*27 + 0*26 + 0*25 + 1*24 + 1*23 + 0*22 + 1*21 + 0*20 = 27 + 24 + 23 + 21 = 128 + 16 + 8 + 2 = 154 • What is 00101001 in decimal? 00101001 = 0*27 + 0*26 + 1*25 + 0*24 + 1*23 + 0*22 + 0*21 + 1*20 = 25 + 23 + 20 = 32 + 8 + 1 = 41 4/30/2018 Pavithran Puthiyapurayil , Maldives National University
- 29. 29 A note on binary numbers • In this slide set we are only dealing with non- negative numbers • The book (section 1.5) talks about two’s- complement binary numbers – Positive (and zero) two’s-complement binary numbers is what was presented here – We won’t be getting into negative two’s- complmeent numbers 4/30/2018 Pavithran Puthiyapurayil , Maldives National University
- 30. 30 How to add binary numbers • Consider adding two 1-bit binary numbers x and y – 0+0 = 0 – 0+1 = 1 – 1+0 = 1 – 1+1 = 10 • Carry is x AND y • Sum is x XOR y • The circuit to compute this is called a half-adder x y Carry Sum 0 0 0 0 0 1 0 1 1 0 0 1 1 1 1 0 4/30/2018 Pavithran Puthiyapurayil , Maldives National University
- 31. 31 The half-adder • Sum = x XOR y • Carry = x AND y x y Sum Carry x y Sum Carry x y Carry Sum 0 0 0 0 0 1 0 1 1 0 0 1 1 1 1 0 4/30/2018 Pavithran Puthiyapurayil , Maldives National University
- 32. 32 Using half adders • We can then use a half-adder to compute the sum of two Boolean numbers 1 1 0 0 + 1 1 1 0 010? 001 4/30/2018 Pavithran Puthiyapurayil , Maldives National University
- 33. 33 How to fix this • We need to create an adder that can take a carry bit as an additional input – Inputs: x, y, carry in – Outputs: sum, carry out • This is called a full adder – Will add x and y with a half-adder – Will add the sum of that to the carry in • What about the carry out? – It’s 1 if either (or both): – x+y = 10 – x+y = 01 and carry in = 1 x y c carry sum 1 1 1 1 1 1 1 0 1 0 1 0 1 1 0 1 0 0 0 1 0 1 1 1 0 0 1 0 0 1 0 0 1 0 1 0 0 0 0 0 4/30/2018 Pavithran Puthiyapurayil , Maldives National University
- 34. 34 HAX Y S C HAX Y S C x y c c s HAX Y S C HAX Y S C x y c The full adder • The “HA” boxes are half-adders x y c s1 c1 carry sum 1 1 1 0 1 1 1 1 1 0 0 1 1 0 1 0 1 1 0 1 0 1 0 0 1 0 0 1 0 1 1 1 0 1 0 0 1 0 1 0 0 1 0 0 1 0 0 0 1 0 0 0 0 0 0 0 s1 c1 4/30/2018 Pavithran Puthiyapurayil , Maldives National University
- 35. 35 The full adder • The full circuitry of the full adder x y s c c 4/30/2018 Pavithran Puthiyapurayil , Maldives National University
- 36. 36 Adding bigger binary numbers • Just chain full adders together HAX Y S C FAC Y X S C FAC Y X S C FAC Y X S C x1 y1 x2 y2 x3 y3 x0 y0 s0 s1 s2 s3 c ... 4/30/2018 Pavithran Puthiyapurayil , Maldives National University
- 37. 37 Adding bigger binary numbers • A half adder has 4 logic gates • A full adder has two half adders plus a OR gate – Total of 9 logic gates • To add n bit binary numbers, you need 1 HA and n-1 FAs • To add 32 bit binary numbers, you need 1 HA and 31 FAs – Total of 4+9*31 = 283 logic gates • To add 64 bit binary numbers, you need 1 HA and 63 FAs – Total of 4+9*63 = 571 logic gates 4/30/2018 Pavithran Puthiyapurayil , Maldives National University
- 38. 38 More about logic gates • To implement a logic gate in hardware, you use a transistor • Transistors are all enclosed in an “IC”, or integrated circuit • The current Intel Pentium IV processors have 55 million transistors! 4/30/2018 Pavithran Puthiyapurayil , Maldives National University
- 39. 39 Flip-flops • Consider the following circuit: • What does it do? 4/30/2018 Pavithran Puthiyapurayil , Maldives National University
- 40. 40 Memory • A flip-flop holds a single bit of memory – The bit “flip-flops” between the two NAND gates • In reality, flip-flops are a bit more complicated – Have 5 (or so) logic gates (transistors) per flip-flop • Consider a 1 Gb memory chip – 1 Gb = 8,589,934,592 bits of memory – That’s about 43 million transistors! • In reality, those transistors are split into 9 ICs of about 5 million transistors each 4/30/2018 Pavithran Puthiyapurayil , Maldives National University
- 41. 41 Hexadecimal • A numerical range from 0-15 – Where A is 10, B is 11, … and F is 15 • Often written with a ‘0x’ prefix • So 0x10 is 10 hex, or 16 – 0x100 is 100 hex, or 256 • Binary numbers easily translate: 4/30/2018 Pavithran Puthiyapurayil , Maldives National University