Logika
- 1. LOGIKA Oleh: ADE APINDO MALIDAH HOLA APRILYANI MARLITA DEPI ADELIA SARI
- 2. Proposisi DEFINISI Proposisi adalah kalimat deklaratif yang bernilai benar (true) atau salah (false), tetapi tidakdapat sekaligus keduanya. Kebenaran atau kesalahan dari sebuah kalimat disebut nilai kebenarannya(truth value). Contoh: 1. 13 adalah bilangan ganjil 2. Soekarno adalah alumnusUGM. 3. 1 + 1 = 2 4. Hari ini adalah hari Rabu 5. Isilah gelas tersebut dengan air! 6. X + 3 = 8 7. x > 3
- 3. Mengkombinasikan Proposisi Misalkan p dan q adalah proposisi. 1.Konjungsi (conjunction) : p dan q Notasi p ⧠q, 1.Disjungsi (disjunction) : p atau q Notasi: p âĻ q, 1.Ingkaran (negation) dari p: tidak p Notasi : âžp P dan q disebut proposisi atomik âĒ Kombinasi p dengan q menghasilkan proposisi majemuk (compound proposition)
- 4. Contoh: Diketahui proposisi -proposisi berikut: p : Hari ini hujan Q : Murid-murid diliburkan dari sekolah maka p ⧠q : Hari ini hujan dan murid-murid diliburkan dari sekolah p âĻ q : Hari ini hujan atau murid-murid diliburkan dari sekolah âžp : Tidak benar hari ini hujan (atau dalam kalimat lain yang lebih lazim: Hari ini tidak hujan)
- 5. Tabel kebenaran Definisi misalkan p dan q adalah proposisi.
- 6. Disjungsi Eksklusif Dari tabel tersebut dapat dibaca proposisi P â q hanya benar jika salah satu, tapi tidak keduanya, dari proposisi atomiknya benar Tabel kebenaran exclusive or
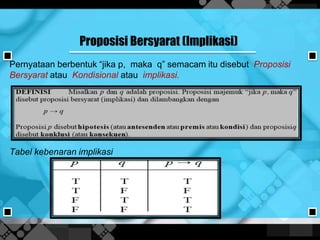
- 8. Proposisi Bersyarat (Implikasi) Pernyataan berbentuk âjika p, maka qâ semacam itu disebut Proposisi Bersyarat atau Kondisional atau implikasi. Tabel kebenaran implikasi
- 9. Contoh: jika saya lulus ujian, maka saya mendapat hadiah dari ayah b. Jika suhu mencapai 80° C, maka alarm akan berbunyi c. Jika anda tidak mendaftar ulang, maka anda dianggap mengundurkan diri
- 10. Cara-cara mengekspresikan implikasi p â q : âĒ Jika p, makaq âĒ Jika p, q âĒp mengakibatkan q (p implies q) âĒq jika p âĒp hanya jika q âĒp syarat cukup untuk q (hipotesis menyatakansyarat cukup(sufficient condition) ) âĒq syarat perlu untuk p (konklusi menyatakan syarat perlu (necessary condition) ) âĒq bilamana p (q whenever p)
- 11. Varian Proposisi Bersyarat Terdapat bentuk implikasi lain yang berkaitan dengan p â q, yaitu proposisi sederhana yang merupakan varian dari implikasi. Ketiga variasi proposisi bersyarat tersebut adalah konvers, invers, dan kontraposisi dari proposisi asal pâq. Konvers (kebalikan) : qâp Invers : ~ pâ~ q Kontraposisi : ~ qâ~ p Contoh: Tentukan konvers, invers, dan kontraposisi dari pernyataan berikut âJika Amir mempunyai mobil, maka ia orang kayaâ Penyelesaian. Konvers: Jika Amir orang kaya, maka ia mempunyai mobil Invers: Jika Amir tidak mempunyai mobil, maka ia bukan orang kaya Kontraposisi: Jika Amir bukan orang kaya, maka ia ia tidak mempunyai mobil
- 12. Bikondisional (Bi-implikasi) Proposisi bersyarat penting lainnya adalah berbentuk âp jika dan hanya jika qâ yang dinamakan bikondisional atau bi-implikasi. Definisi bikondisional dikemukakan sebagai berikut. Pernyataan pâq adalah benar bila p dan q mempunyai nilai kebenaran yang sama, yakni pâq benar jika p dan q keduanya benar atau p dan q keduanya salah. Tabel kebenaran bikondisional
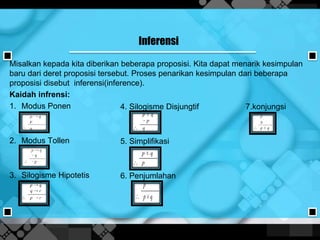
- 13. Inferensi Misalkan kepada kita diberikan beberapa proposisi. Kita dapat menarik kesimpulan baru dari deret proposisi tersebut. Proses penarikan kesimpulan dari beberapa proposisi disebut inferensi(inference). Kaidah infrensi: 1. Modus Ponen 2. Modus Tollen 3. Silogisme Hipotetis 4. Silogisme Disjungtif 7.konjungsi 5. Simplifikasi 6. Penjumlahan
- 14. Argumen Argumen adalah suatu deret proposisi yang dituliskan sebagai