Magic graph
- 1. MAGIC GRAPH Materi mata kuliah Teori Graph Dosen pengampu : Erika Laras Astutinigntyas,M.Pd. Disusun Oleh : Nama : Diyah Sri Hariyanti NIM : 1051500083 Kelas : 5C PROGRAM STUDI PENDIDIKAN MATEMATIKA FAKULTAS KEGURUAN DAN ILMU PENDIDIKAN UNIVERSITAS VETERAN BANGUN NUSANTARA SUKOHARJO 2012
- 2. MAGIC GRAPH A. Definisi dan Notasi Semua graph diganggap tidak mempunyai isolated vertex, edge paralel, dan loops. Kata cycle dan patch dapat diartikian sebagai simple cycle dan simple path pada sebuah graph. Untuk setiap graph, kita dapat memberikan nomor yang kita sebuah bobot dari edge tersebut. Graph tersebut dapat disebut Semi Graph jika dapat memilih bobot dari edge dan nomor s untuk vertex lainnya jumlah dari bobot dari edge tersebut sama dengan s. Sebuah Graph disebut ajaib jika dapat diberi bobot yang berbeda. Meninjau bahwa vertex berderajat 1 di semi magic graph memerlukan ujung titik dari isolated edge. Magic graph dapat berisi lebih banyak dari 1 isolated edge. Subgraph F dapat menyumbangkan berupa skeleton pada graph G, jika semua vertex dari G dan tidak ada isolated vertex di F. 1-2skeleton adalah kerangka dari semua vertex yang mempunyai derajat 1 atau 2 dan untuk komponen derajat lain dari vertex itu adalah sama. Dengan kata lain 1-2-skeleton hanya terdiri dari isolated edge dan simple cycle, untuk 1-2-skeleton kita dapat membagi semua edge dari grpah menjadi 3 group: edge yang termasuk cycle dari F (kita beri simbol F c); edge yang termasuk part linear dari F , kita beri simbol F (contoh: isolated edge di F); dan edge yang tidak termasuk di F. Kita dapat mengatakan bahwa 1-2-skeleton memisahkan edge e1 dan e2, jika kedua edge termasuk dari 2 group yang berbeda. Dengan kata lain setidaknya mereka merupakan bagian dari F tapi lebih banyak merupakan Fc dan merupakan F. Kita akan menggunakan notasi: C n untuk cycle dengan edge (n>3);
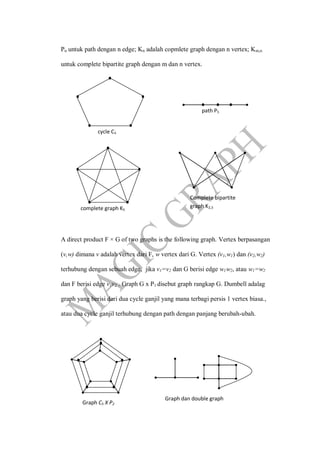
- 3. Pn untuk path dengan n edge; Kn adalah copmlete graph dengan n vertex; Km,n untuk complete bipartite graph dengan m dan n vertex. path P5 cycle C5 complete graph K5 Complete bipartite graph K2,3 A direct product F G of two graphs is the following graph. Vertex berpasangan (v,w) dimana v adalah vertex dari F, w vertex dari G. Vertex (v1,w1) dan (v2,w2) terhubung dengan sebuah edge, jika v1=v2 dan G berisi edge w1 w2, atau w1=w2 dan F berisi edge v1v2 . Graph G x P1 disebut graph rangkap G. Dumbell adalag graph yang berisi dari dua cycle ganjil yang mana terbagi persis 1 vertex biasa., atau dua cycle ganjil terhubung dengan path dengan panjang berubah-ubah. Graph C5 X P2 Graph dan double graph
- 4. Dum-bell Kita akan mempertimbangkan sebuah graf G V G , E G mengorientasikan adanya loops, berbagai edges atau isolated vertices. Jika ada suatu pemetaan f dari satuan edges E G kedalam bilangan real positif.: i. ii. f ei f e j untuk semua ei e j ; ei ,e j E G ワ v, e f e r untuk semua v V G eE G 1 Dimana v,e 0 Kemudian graph G disebut magic (ajaib). Pemetaan f disebut pemberian label terhadap G dan nilai r adalah indeks dari label f. Kita katakana bahwa sebuah graph G adalah semimagic jika ada pemetaan f terhadap bilangan real positif yang hanya memenuhi kondisi (ii). Jika semimagic graph G mempunyi sebuah label dengan indeks r ,kita akan mengatakan bahwa G mempunyai indeks r. B. MAGIC LABELING Beberapa pelabelan pada graph sebenarnya digeneralisasi dari ide persegi ajaib (magic square). Suatu graph terhubung disebut semi-magic jika terdapat pelabelan pada sisi-sisinya dengan bilangan bulat sehingga untuk masing-masing
- 5. titik v, maka jumlah label sisi yang incident dengan v adalah sama untuk semua titik v. Pelabelan semi-magic yang memetakan sisi ke himpunan bilangan bulat positif yang berbeda disebut pelabelan magic. Pelabelan magic disebut super magic jika label sisi adalah bilangan bulat positif yang berurutan. Graph berlabel ajaib adalah graph yang memiliki weight (W) atau berat yang sama. Contoh: 5 2 3 1 4 W1 = 1 + 5 + 3 = 9 W2 = 3 + 2 + 4 = 9 Bobot W1 dan W2 adalah sama, yaitu sama-sama 9. Maka graph ini disebut graph ajaib (Magic Graph). Berikut ini beberapa jenis pelabelan ajaib pada suatu graf : 1. Misalkan G graf dengan himpunan titik V dan himpunan sisi E. Banyak titik di G adalah p dan banyak sisi di G adalah q. Pelabelan titik sisi ajaib (edge-magic vertex labeling) pada graf G adalah pemetaan bijektif 了 dari V pada himpunan {1, 2, 3, , p} sehingga untuk sebarang sisi (x y) di G berlaku + = untuk suatu konstanta k. Selanjutnya k disebut konstanta ajaib pada G dan G disebut graf titik sisi ajaib.
- 6. Contoh: 1 2 Gambar 1 Pelabelan Titik Sisi Ajaib Graf P2 Pelabelan titik sisi ajaib graf P2 pada gambar 1 mempunyai k=3. 2. Misalkan G graf dengan himpunan titik V dan himpunan sisi E. Banyak titik di G adalah p, banyak sisi di G adalah q dan h merupakan banyak titik dan sisi pada graf G atau h = p+q. Pelabelan total titik ajaib (vertex-magic total labeling) pada graf G adalah pemetaan bijektif dari VE pada himpunan {1, 2, 3, , h} sehingga untuk sebarang titik x di G berlaku + 透 ヰ = dengan y merupakan titik yang berdekatan dengan titik x. Selanjutnya k disebut konstanta ajaib pada G dan G disebut graf total titik ajaib. 13 Contoh : 3 14 10 20 2 1 16 18 9 12 17 19 5 4 8 6 15 21 11 7 Gambar 2. Pelabelan Total Titik Ajaib Graf K6 Pelabelan total titik ajaib graf K6 pada gambar 2 mempunyai k=66.
- 7. 3. Misalkan G graf dengan himpunan titik V dan himpunan sisi E. Banyak titik di G adalah p dan banyak sisi di G adalah q. Pelabelan sisi titik ajaib (vertex-magic edge labeling) pada graf G adalah pemetaan bijektif 了 dari E pada himpunan {1, 2, 3, , q} sehingga untuk sebarang titik x di G berlaku 透 ヰ = dengan y merupakan titik yang berdekatan dengan titik x. Selanjutnya k disebut konstanta ajaib pada G dan G disebut graf sisi titik ajaib. Contoh: 1 Gambar 3. Pelabelan Sisi Titik Ajaib Graf P2 Pelabelan sisi titik ajaib Graf P2 pada gambar 3 mempunyai k=1. 4. Misalkan G graf dengan himpunan titik V dan himpunan sisi E. Banyak titik di G adalah p, banyak sisi di G adalah q dan h merupakan banyak titik dan sisi pada graf G atau h = p+q. Pelabelan total sisi ajaib (edge-magic total labeling) pada graf G adalah pemetaan bijektif 了 dari V E pada himpunan {1, 2, 3, , h} sehingga untuk sebarang sisi (xy) di G berlaku + ヰ + () = untuk suatu konstanta k. Selanjutnya k disebut konstanta ajaib pada G dan G disebut graf total sisi ajaib.
- 8. Contoh : 1 10 9 3 4 6 8 5 7 2 Gambar 4. Pelabelan Total Sisi Ajaib Graf C5 Pelabelan total sisi ajaib graf C5 pada gambar 4 mempunyai k=14.