Magical
- 1. 魔法陣 原案 : fura2 解答 : fura2 解説 : fura2
- 2. 問題概要 ● こんな感じの魔法阵の青い部分の面积を求めよ
- 3. 解法 ● 二种类あります
- 4. 解法 1
- 5. 解法 1 ● まず、多角形が三角形のときを考える ● f(r) := ( 三角形と半径 r の円の共通部分の面積 ) とする f(r)
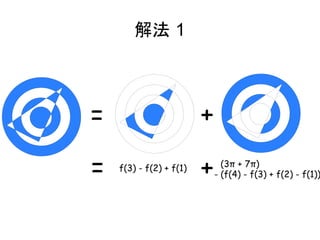
- 6. 解法 1 = + = f(3) - f(2) + f(1) + (3π + 7π) - (f(4) - f(3) + f(2) - f(1))
- 7. 解法 1 ● 一般の単純多角形のとき ● 多角形を三角形分割すれば、三角形の場合に帰 着できる – サイズが小さいので、三角形分割は計算量が悪い方法 でやってもいい。O(n3 log n) くらいまでなら何でもOK – 一応、理論上は O(n) でできるらしい
- 8. 解法 2
- 9. 解法 2 ● 適当な点 c を中心として、偏角方向に平面走査す る – イベント点は、多角形の頂点、円と多角形の交点
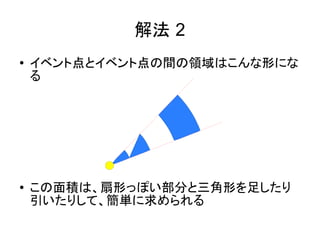
- 10. 解法 2 ● イベント点とイベント点の間の領域はこんな形にな る ● この面積は、扇形っぽい部分と三角形を足したり 引いたりして、簡単に求められる
- 11. 解法 2 ● 中心 c の選び方について – 扇形っぽい部分の面積を求めやすくするため、c は半 径 1 の円の内部にとるのがいい – c を原点とすると、扇形っぽい部分が本当に扇形になる けど、多角形の頂点が原点にあるケースがコーナー ケースになりうるので注意
- 12. 提出状況 ● AC Rate – 0 % (0/2) ● First Acceptance – Onsite: なし – All: なし