Matematik tambahan tingkatan 4 fungsi kuadratik {add math form 4 - quadractic function}
- 1. www.tutorsah.com 1 1. Fungsi Kuadratik dan Grafnya Bentuk am Fungsi Kuadratik. 2 ( )f x ax bx c’ĆĮ ’Ć½ ’Ć½ a, b, c = pemalar (constant) x = pembolehubah ØÆé ŌēĀ 0
- 2. www.tutorsah.com 2 Memplot graf fungsi kuadratik 2 ( ) 2 3f x x x’ĆĮ ’Ć½ ’ĆŁ Paksi-y (menegak) Paksi-x (mendatar) Bagi memplot graf fungsi kuadratik, beberapa titik (koordinat) diperlukan: x -3 -2 -1 0 1 2 3 f(x) 0 -3 -4 -3 0 5 12 2 2 Jika 2: ( ) 2 3 (2) 2(2) 3 5x f x x x’ĆĮ ’ĆĮ ’Ć½ ’ĆŁ ’ĆĮ ’Ć½ ’ĆŁ ’ĆĮ 2 2 Jika 3: ( ) 2 3 ( 3) 2( 3) 3 0x f x x x’ĆĮ ’ĆŁ ’ĆĮ ’Ć½ ’ĆŁ ’ĆĮ ’ĆŁ ’Ć½ ’ĆŁ ’ĆŁ ’ĆĮ
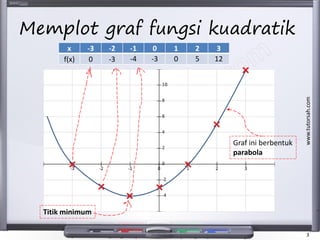
- 3. www.tutorsah.com 3 Memplot graf fungsi kuadratik x -3 -2 -1 0 1 2 3 f(x) 0 -3 -4 -3 0 5 12 Titik minimum Graf ini berbentuk parabola
- 4. www.tutorsah.com 4 Memplot graf fungsi kuadratik 2 ( ) 2 3f x x x’ĆĮ ’Ć½ ’ĆŁ Perhatikan graf berbentuk ŌĆśUŌĆÖ bagi fungsi kuadratik yang pemalar ŌĆśaŌĆÖ bernilai positif. 1 ( 0)a ’ĆĮ ’ĆŠ Bagi fungsi kuadratik yang pemalar ŌĆśaŌĆÖ bernilai negatif, grafnya akan berbentuk ŌĆśnŌĆÖ. 1 ( 0)a ’ĆĮ ’ĆŁ ’Ć╝ 2 ( ) 2 3f x x x’ĆĮ ’ĆŁ ’Ć½ ’ĆŁ Titik minimum Titik maksimum Akan mempunyai ŌĆśtitik maksimumŌĆÖ. Akan mempunyai ŌĆśtitik minimumŌĆÖ.
- 5. www.tutorsah.com 5 2. Nilai Maksimum dan Nilai Minimum Fungsi Kuadratik Nilai maksimum atau nilai minimum boleh ditentukan melalui kaedah Penyempurnaan Kuasa Dua. Bentuk am Penyempurnaan Kuasa Dua: 2 ( ) ( )f x a x p q’ĆĮ ’Ć½ ’Ć½ Nilai minimum / maksimum (koordinat paksi-y) Nilai ŌĆśaŌĆÖ akan menentukan bentuk graf ŌĆśuŌĆÖ atau ŌĆśnŌĆÖ.
- 6. www.tutorsah.com 6 2 ( ) 2 3f x x x’ĆĮ ’Ć½ ’ĆŁContoh bagi fungsi kuadratik berikut: 2 2 2 2 2 2 2 2 (2 2) ( ( ) 2 3 [ 2 ] 3 [ 2 ] 3 ( 1) 2 2) (1) (1) 4 f x x x x x x x x ’éĖ ’éĖ ’ĆĮ ’Ć½ ’ĆŁ ’ĆĮ ’Ć½ ’Ć½ ’ĆŁ ’ĆŁ ’ĆĮ ’Ć½ ’Ć½ ’ĆŁ ’ĆŁ ’ĆĮ ’Ć½ ’ĆŁ Bentuk am: 2 ( ) ( 1) 4f x x’ĆĮ ’Ć½ ’ĆŁ Pemalar ŌĆśaŌĆÖ = 1 (>0), oleh itu graf berbentuk ŌĆśuŌĆÖ Bagi graf berbentuk ŌĆśuŌĆÖ, titik minimum diperoleh
- 7. www.tutorsah.com 7 3. Lakaran Graf Fungsi Kuadratik Untuk melakar graf fungsi kuadratik, kita perlukan titik minimum / maksimum dan beberapa ŌĆśtitik persilanganŌĆÖ antara paksi. 2 ( ) ( 1) 4f x x’ĆĮ ’Ć½ ’ĆŁ Nilai minimum (koordinat paksi-y): 2 2 2 ( ) 4 ( 1) 4 4 ( 1) 4 4 ( 1) 0 1 0 1 f x x x x x x ’ĆĮ ’ĆŁ ’Ć½ ’ĆŁ ’ĆĮ ’ĆŁ ’Ć½ ’ĆĮ ’ĆŁ ’Ć½ ’Ć½ ’ĆĮ ’Ć½ ’ĆĮ ’ĆĮ ’ĆŁ Oleh itu, titik minimum terletak di koordinat (-1, -4)
- 8. www.tutorsah.com 8 2 ( ) ( 1) 4f x x’ĆĮ ’Ć½ ’ĆŁ Pintasan-y berlaku apabila x = 0 2 2 2 ( ) ( 1) 4 0 ( 1) 4 4 ( 1) 4 1 2 1 f x x x x x x ’ĆĮ ’Ć½ ’ĆŁ ’ĆĮ ’Ć½ ’ĆŁ ’ĆĮ ’Ć½ ’ĆĮ ’Ć½ ’é▒ ’ĆĮ ’Ć½ Pintasan-x berlaku apabila f(x) = 0 1 2 2 1 1 x x ’Ć½ ’ĆĮ ’Ć½ ’ĆĮ ’Ć½ ’ĆŁ ’ĆĮ 1 2 2 1 3 x x ’Ć½ ’ĆĮ ’ĆŁ ’ĆĮ ’ĆŁ ’ĆŁ ’ĆĮ ’ĆŁ 2 2 ( ) ( 1) 4 (0 1) 4 1 4 3 f x x’ĆĮ ’Ć½ ’ĆŁ ’ĆĮ ’Ć½ ’ĆŁ ’ĆĮ ’ĆŁ ’ĆĮ ’ĆŁ Koordinat (1, 0) Koordinat (-3, 0) Koordinat (0, -3)
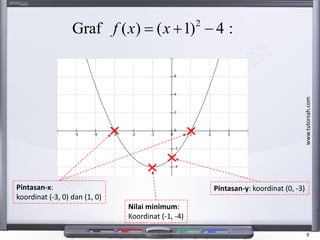
- 9. www.tutorsah.com 9 2 Graf ( ) ( 1) 4 :f x x’ĆĮ ’Ć½ ’ĆŁ Nilai minimum: Koordinat (-1, -4) Pintasan-x: koordinat (-3, 0) dan (1, 0) Pintasan-y: koordinat (0, -3)
- 10. www.tutorsah.com 10 4. Ketaksamaan Kuadratik 2 2 3 0 ( 3)( 1) 0 x x x x ’Ć½ ’ĆŁ ’Ć╝ ’Ć½ ’ĆŁ ’Ć╝ ( 3) 0 3 x x ’Ć½ ’Ć╝ ’ĆŠ ’ĆŁ ( 1) 0 1 x x ’ĆŁ ’Ć╝ ’Ć╝ 3 1x’ĆŁ ’Ć╝ ’Ć╝
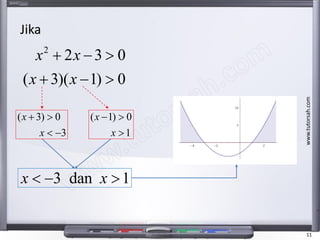
- 11. www.tutorsah.com 11 2 2 3 0 ( 3)( 1) 0 x x x x ’Ć½ ’ĆŁ ’ĆŠ ’Ć½ ’ĆŁ ’ĆŠ ( 3) 0 3 x x ’Ć½ ’ĆŠ ’Ć╝ ’ĆŁ ( 1) 0 1 x x ’ĆŁ ’ĆŠ ’ĆŠ 3 dan 1x x’Ć╝ ’ĆŁ ’ĆŠ Jika




![www.tutorsah.com
6
2
( ) 2 3f x x x’ĆĮ ’Ć½ ’ĆŁContoh bagi fungsi kuadratik berikut:
2
2
2
2 2
2
2
2
(2 2) (
( ) 2 3
[ 2 ] 3
[ 2 ] 3
( 1)
2 2)
(1) (1)
4
f x x x
x x
x x
x
’éĖ ’éĖ
’ĆĮ ’Ć½ ’ĆŁ
’ĆĮ ’Ć½ ’Ć½ ’ĆŁ ’ĆŁ
’ĆĮ ’Ć½ ’Ć½ ’ĆŁ ’ĆŁ
’ĆĮ ’Ć½ ’ĆŁ
Bentuk am:
2
( ) ( 1) 4f x x’ĆĮ ’Ć½ ’ĆŁ
Pemalar ŌĆśaŌĆÖ = 1 (>0),
oleh itu graf berbentuk ŌĆśuŌĆÖ Bagi graf berbentuk ŌĆśuŌĆÖ,
titik minimum diperoleh](https://image.slidesharecdn.com/matematiktambahantingkatan4-fungsikuadratikaddmathform4-quadracticfunction-190228084346/85/Matematik-tambahan-tingkatan-4-fungsi-kuadratik-add-math-form-4-quadractic-function-6-320.jpg)