�ݺ�ߣ

Sampel Acak dan Statistik
Bahan Kuliah II2092 Probabilitas dan Statistik
Oleh: Rinaldi Munir
Sekolah Teknik Elektro dan Informatika ITB
1

Populasi
• Dalam survey statistik, hasil pengamatan dicatat dalam
numerik. Obyek yang diamati bisa manusia, hewan, atau
benda lainnya.
• Keseluruhan pengamatan yang diteliti membentuk apa yang
disebut populasi atau universum.
disebut populasi atau universum.
• Suatu populasi terdiri atas keseluruhan pengamatan yang
menjadi perhatian.
• Contoh: pemilih di sebuah kota disurvey, berapa orang yang
akan memilih partai tertentu. Populasinya adalah seluruh
pemilih di kota tersebut.
2

• Ukuran populasi menyatakan banyaknya pengamatan di
dalam populasi. Jika jumlah pemilih 20000 orang, maka
ukuran populasinya dikatakan 20000 orang.
• Tiap pengamatan di dalam populasi merupakan nilai dari
suatu peubah acak X dengan distribusi peluang f(x).
• Dalam praktek, mengamati himpunan seluruh
pengamatan di dalam populasi tidak praktis atau malah
tidak mungkin. Selain itu faktor biaya yang tinggi juga
menjadi penyebabnya.
3

• Oleh karena itu, kita terpaksa menggunakan
sebagian pengamatan dari populasi untuk menarik
inferensi statistik tentang populasi tersebut.
• Himpunan bagian dari populasi dinamakan sampel.
• Agar inferensi dari sampel tentang populasi valid,
• Agar inferensi dari sampel tentang populasi valid,
maka sampel haruslah diambil mewakili populasi.
• Untuk mencegah timbulnya bias dalam prosedur
sampling, maka sebaiknya menggunakan sampel
acak.
4

• Sampel acak berarti pengamatan dilakukan secara
bebas satu sama lain dan acak.
• Misalkan X1, X2,…, Xn merupakan n peubah acak
bebas yang masing-masing berdistribusi peluang f(X).
X1, X2,…, Xn didefinisikan sebagai sampel acak ukuran
X1, X2,…, Xn didefinisikan sebagai sampel acak ukuran
n dari populasi f(X) dan distribusi peluang
gabungannya ditulis sebagai
f(X1, X2, .., Xn) = f(X1) f(X2) .. f(Xn)
5

• Contoh: dari sebuah pabrik batere dipilih secara acak
n = 8 batere yang diproduksi dengan keadaan yang
sama, kemudian umurnya dicatat: x1 adalah umur
batere pertama, x2 adalah umur batere kedua, dan
seterusnya. Maka, x1, x2, …, x8 merupakan nilai
sampel acak X1, X2, …, X8 . Bila dianggap populasi
umur batere berditsribusi normal, nilai yang mungkin
umur batere berditsribusi normal, nilai yang mungkin
untuk xi, i = 1, 2, …, 8, akan tetap sama dengan pada
populasi semula. Dan karena itu Xi mempunyai
distribusi normal yang tepat sama dengan X.
6

Statistik
• Apa yang dimaksud dengan statistik?
• Tujuan utama memilih sampel acak adalah untuk
mendapatkan keterangan mengenai parameter populasi yang
tidak diketahui.
tidak diketahui.
• Misalkan kita ingin mengetahui proporsi penduduk Indonesia
yang menyukai permen coklat merek ABC.
• Mutahil menanyakan kepada seluruh penduduk apakah
mereka menyukai permen coklat tersebut.
• Oleh karena itu diambil sampel acak yang banyak kemudian
dilakukan pengukuran parameter yang diinginkan.
7

• Dalam praktek, parameter p yang menggambarkan
proporsi sebenarnya dihampiri dengan parameter
pada sampel acak tersebut.
• Nilai ini kemudian dipakai untuk menarik kesimpulan
mengenai proporsi p yang sesungguhnya.
• Jadi, merupakan fungsi dari nilai pengamatan dalam
sampel acak.
p̂
p̂
p̂
sampel acak.
• Karena banyak kemungkinan sampel acak yang dapat
diambil dari populasi yang sama, maka tentunya akan
berbeda sedikit antara sampel acak yang satu dengan
sampel acak yang lain.
• Dengan kata lain, adalah nilai dari suatu peubah acak
yang kita nyatakan dengan P. Peubah acak seperti ini
dinamakan statistik
p̂
p̂
8

• Definisi. Setiap fungsi dari peubah acak yang
membentuk suatu sampel acak disebut statistik.
• Dengan kata lain, statistik merupakan peubah acak
yang nilainya hanya bergantung pada sampel acak
yang diamati.
yang diamati.
• Statistik yang paling sering dipakai untuk
menggambarkan ukuran padanan pada suatu sampel
acak adalah rataan, median, modus, jangkauan,
variansi, dan simpangan baku.
9

Rataan (mean)
• Definisi. Bila X1, X2, …, Xn menyatakan sampel acak berukuran n,
maka rataan sampel dinyatakan oleh statistik:
• Contoh 1. Hitung rataan dari sampel acak dari 8 orang
wisudawan ITB yang dicatat umurnya, yaitu 22, 21, 24, 22, 23,
n
X
X
n
i
i
∑
=
= 1
wisudawan ITB yang dicatat umurnya, yaitu 22, 21, 24, 22, 23,
25, 24, 22.
Jawaban:
10
875
.
22
8
22
24
25
23
22
24
21
22
=
+
+
+
+
+
+
+
=
x

Median
• Definisi. Bila X1, X2, …, Xn menyatakan sampel acak berukuran
n, diurutkan membesar menurut besarnya, maka median
sampel ditentukan sebagai statistik
=
X
~
• Contoh 2. Tentukan median dari usia wisudawan pada
Contoh 1 di atas.
Jawaban: Urutkan data pengamatan terlebih dahulu:
21, 22, 22, 22, 23, 24, 24, 25
Karena n genap, maka mediannya:
11
5
.
22
2
23
22
~ =
+
=
x

Modus
n, maka modus M ialah suatu nilai sampel yang paling sering
muncul atau frekuensinya paling tinggi. Modus mungkin tidak
ada, dana kalaupun ada mungkin tidak tunggal.
• Contoh 3. Tentukan modus dari usia wisudawan pada Contoh
• Contoh 3. Tentukan modus dari usia wisudawan pada Contoh
1 di atas.
Jawaban: Dari data pengamatan: 22, 21, 24, 22, 23, 25, 24, 22,
maka 22 adalah modusnya karena 22 muncul paling banyak
yaitu 3 kali.
12

• Contoh 4. Bila data pengamatannya bertambah menjadi 10
orang sehingga diperoleh 22, 21, 24, 22, 23, 25, 24, 22, 24, 23,
maka modunya ada 2 yaitu 22 dan 24 karena keduanya paling
sering muncul. Statistik ini disebut dwimodus.
• Contoh 5. Bila pengamatan dari 8 sampel acak wisuadawan
yang lain menghasilkan data pengamatan usia sebagai berikut
yang lain menghasilkan data pengamatan usia sebagai berikut
22, 21, 24, 23, 20, 25, 26, 27, maka modusnya tidak ada
karena setiap nilai muncul satu kali.
13

Jangkauan
• Definisi. Jangkauan atau rentangan dari sampel acak X1, X2,
…, Xn didefinisikan sebagai statistik X(n) – X(1) , bila X(n) dan X(1)
masing-masing menyatakan pengamatan yang terbesar dan
terkecil dari sampel.
• Contoh 6. Dari data pengamatan usia wisudawan: 22, 21, 24,
• Contoh 6. Dari data pengamatan usia wisudawan: 22, 21, 24,
22, 23, 25, 24, 22, terlihat usia tertinggi = 25 dan usia
terendah = 21, sehingga jangkauan = 25 – 21 = 4.
14

Variansi
n, maka variansi sampel didefinisikan sebagai statistik:
• Contoh 7. Hitung variansi dari data pengamatan usia
• Contoh 7. Hitung variansi dari data pengamatan usia
wisudawan pada Contoh 1 di atas.
Jawaban: Dari data pengamatan 22, 21, 24, 22, 23, 25, 24, 22
sudah diperoleh rataanya . Variansinya adalah
15
875
.
22
=
x
=
−
+
+
−
+
−
=
−
−
=
∑
=
7
)
875
.
22
22
(
...
)
875
.
22
21
(
)
875
.
22
22
(
1
8
)
875
.
22
(
2
2
2
8
1
2
2 i
i
X
s

• Untuk menghindari kesalahan akibat pembulatan,
maka alternatif menghitung variansi adalah dengan
rumus:
)
1
(
1
2
1
2
2
−






−
=
∑ ∑
= =
n
n
X
X
n
S
n
i
n
i
i
i
16

Simpangan Baku
• Simpangan baku sampel dinyatakan dengan S adalah akar
positif variansi sampel.
• Contoh 8. Hitunglah variansi dari data acak 3, 4, 5, 6, 6, dan 7
yang menyatakan banyaknya ikan hasil pancingan dari sampel
acak 6 pengail di sebuah sungai
acak 6 pengail di sebuah sungai
Jawaban:
Jadi, dan S = √(13/6) = 1.47
17
31
X
,
171
,
6
6
1
i
6
2
=
=
= ∑
∑ =
= i
i
i
i
X
n
6
13
)
5
)(
6
(
)
31
(
)
171
)(
6
( 2
2
=
−
=
S

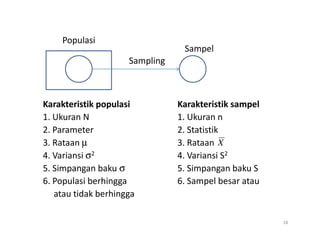
Populasi
Karakteristik populasi Karakteristik sampel
1. Ukuran N 1. Ukuran n
Sampling
Sampel
2. Parameter 2. Statistik
3. Rataan µ 3. Rataan
4. Variansi σ2 4. Variansi S2
5. Simpangan baku σ 5. Simpangan baku S
6. Populasi berhingga 6. Sampel besar atau
atau tidak berhingga
18
X

Distribusi Sampel
• Bidang statistika inferensi pada dasarnya berkenaan
dengan perampatan dan hasil prediksi.
• Kita menghitung suatu statistik dari sampel yang
dipilih dari populasi, dan dari statistik ini kita
membuat pernyataan yang mungkin benar atau tidak
mengenai nilai parameter populasi.
• Contoh: berdasarkan pendapat beberapa orang yang
diwawancarai sebelum Pilkada di Bandung, 60% dari
pemilih akan memilih calon tertentu.
19

• Karena statistik merupakan peubah acak yang
tergantung hanya pada sampel yang diamati, maka
tentulah ada distribusi peluangnya.
• Definisi. Distribusi peluang suatu statistik disebut
distribusi sampel.
• Definisi. Simpangan baku distribusi sampel suatu
statistik disebut galat baku dari statistik tersebut.
• Distribusi sampel suatu statistik bergantung pada
ukuran populasi, ukuran sampel, dan, metode
memilih sampel.
20

Distribusi Sampel dari Rataan
• Distribusi sampel pertama yang penting adalah distribusi
sampel dari rataan.
• Contoh, misalkan kita mempunyai populasi berupa bilangan,
yaitu 2, 3, 6, 8, 11. Populasi ini berukuran berhingga yaitu N =
5. Misalkan kita ambil sampel acak berukuran n = 2, tanpa
pengembalian, maka kombinasi sampel yang berlainan adalah
pengembalian, maka kombinasi sampel yang berlainan adalah
sebanyak C(5, 2) = 5!/(2!3!) = 10. Kesepuluh jenis sampel
tersebut dan rataanya adalah sebagai berikut:
Sampel 1: 2 dan 3; rataan =
… dst hingga sampel 10
21
5
.
2
2
/
)
3
2
(
1 =
+
=
X
0
.
4
2
/
)
6
2
(
2 =
+
=
X
0
.
5
2
/
)
8
2
(
3 =
+
=
X

• Perhatikanlah bahwa rataan mempunyai
nilai yang berbeda-beda sehingga rataan
membentuk suatu sampel acak tersendiri yaitu yang
disebut sampel rataan, oleh karena itu kita bisa
menentukan rataan dan simpangan baku dari sampel
rataan ini.
10
2
1 ,...,
, X
X
X
10
2
1 ,...,
, X
X
X
X
• Sampel rataan mempunyai distribusi peluang sendiri
yang dinamakan distribusi sampel rataan.
• Definisi. Distribusi peluang disebut distribusi sampel
dari rataan dan galat baku rataan adalah simpangan baku
dari distribusi sampel .
22
X
X

• Misalkan sampel acak yang berisi n pengamatan diambil dari
populasi normal dengan rataan µ dan variansi σ2.
• Sampel acak berukuran n diambil secara berulang-ulang, lalu
rataan setiap sampel dihitung, yaitu .
• Setiap pengamatan , i = 1, 2, …, n, dari sampel acak
tersebut akan berdistribusi normal yang sama dengan
populasi yang diambil sampelnya.
n
X
X
X ,...,
, 2
1
i
X
• Jadi, dapat disimpulkan
berdistribusi normal dengan rataan
variansi dan simpangan baku
23
n
X
X
X
X n
+
+
+
=
...
2
1
µ
µ
µ
µ
µ =
+
+
+
=
n
X
...
n
n
X
2
2
2
2
2
2 ... σ
σ
σ
σ
σ =
+
+
+
=
n
X
σ
σ =

• Contoh 9. Suatu sampel acak berukuran n = 10
diambil tanpa pengembalian dari populasi tak
berhingga yang berdistribusi normal dengan rataan
5.5 dan simpangan baku 2.92, setiap sampel lalu
dihitung rataannya. Tentukan rataan dan simpangan
baku dari sampel rataan tersebut.
Jawaban: Sampel rataan tersebut mempunyai
rataan:
simpangan baku:
24
5
.
5
=
= µ
µX
92
.
0
10
92
.
2
=
=
=
n
X
σ
σ

• Bila populasi yang disampel tidak diketahui distribusinya,
maka distribusi sampel masih akan berdistribusi hampir
normal (mendekati distribusi normal) dengan rataan µ dan
variansi σ2/n asalkan ukuran sampelnya besar.
• Hal ini dinyatakan oleh Teorema Limit Pusat sebagai berikut:
Teorema Limit Pusat.
Bila rataan dari sampel acak ukuran n yang diambil dari
X
X
Bila rataan dari sampel acak ukuran n yang diambil dari
populasi dengan rataan µ dan variansi σ2 yang berhingga,
maka bentuk limit dari distribusi
bila n →∞, ialah distribusi normal baku n (z; 0, 1)
25
X

• Dalam statistik, sampel dikatakan berukuran besar jika n ≥ 30.
• Hampiran normal untuk umumnya cukup baik jika n ≥ 30,
terlepas dari bentuk populasi (normal atau bukan).
• Bila n < 30, hampirannya hanya akan baik bila populasinya tidak
• jauh berbeda dengan normal.
• Bila populasinya diketahui normal, maka distribusi sampel
akan tetap berdistribusi normal terlepas dari ukuran
X
X
akan tetap berdistribusi normal terlepas dari ukuran
sampelnya.
• Contoh 10. Suatu perusahaan memproduksi bola lampu yang
umurnya berdistribusi hampir normal dengan rataan 800 jam
dan simpangan baku 40 jam. Hitunglah peluangnya bahwa
suatu sampel acak dengan 16 bola lampu akan mempunyai
umur rata-rata kurang dari 775 jam.
26

Jawaban: Secara hampiran, distribusi sampel akan
berdistribusi normal dengan = 800 dan = 40/ = 10.
Peluang yang dicari diberikan oleh luas daerah yang dihitami
pada gambar. Nilai z yang berpadanan dengan = 775 adalah
sehingga
P( <775) = P(z< -2,5)
P( <775) = P(z< -2,5)
= 0,0062
Gambar 1. Luas Daerah Untuk Contoh 10
27

• Contoh 11. Diketahui sebuah populasi berdistribusi seragam
diskrit:
Hitunglah peluang bahwa sampel acak berukuran 36, yang
dipilih dengan pengembalian, akan menghasilkan rataan
sampel lebih besar dari 1.4 tetapi lebih kecil dari 1.8 bila





=
=
lainnya
,
0
3
,
2
,
1
,
0
,
4
1
)
(
x
x
f
sampel lebih besar dari 1.4 tetapi lebih kecil dari 1.8 bila
rataan diukur (dibulatkan) sampai persepuluhan terdekat.
Jawaban: Rataan dan variansi dihitung dengan rumus yang
terdapat pada materi distribusi seragam diskrit, dan diperoleh
µ = (0 + 1 + 2 + 3)/4 = 3/2 = 1.5
28

dan
σ2 =
Distribusi sampel dapat dihampiri dengan distribusi normal
dengan rataan
= 3/2 dan
Dengan mengambil akarnya diperoleh simpangan baku
4
/
5
4
)
2
/
3
3
(
)
2
/
3
2
(
)
2
/
3
1
(
)
2
/
3
0
( 2
2
2
2
=
−
+
−
+
−
+
−
144
/
5
/
2
2
=
= n
X
σ
σ
Dengan mengambil akarnya diperoleh simpangan baku
= 0.186
Peluang yang ditanyakan adalah
P(1.4 < < 1.8) = ?
Luas daerah yang dimaksudkan terletak antara dan
29
45
.
1
1 =
x
75
.
1
2 =
x

Lakukan transformasi ke peubah z terlebih dahulu:
z1 = (1.45 – 1.5)/0.186 = -0.27
z2 = (1.75 – 1.5)/0.186 = 1.27
Jadi,
P(1.4 < < 1.8) ≅ P(-0.27 < Z < 1.34)
= P(Z < 1.34) – P(Z < -0.27)
= P(Z < 1.34) – P(Z < -0.27)
= 0.9099 – 0.3936
= 0.5163
30

Teorema (Distribusi Sampel dari Selisih Dua Rataan)
• Bila sampel bebas ukuran n1 dan n2 diambil secara acak dari dua
populasi, diskrit maupun kontinu, masing-masing dengan rataan
dan dan , variansi dan , maka distribusi sampel dari
selisih rataan, , berdistribusi hampir normal, rataan dan
variansi diberikan oleh
dan
dan
sehingga
secara hampiran merupakan peubah normal baku.
31

• Jika n1 dan n2 keduanya lebih besar atau sama
dengan 30, hampiran normal untuk distribusi
sangat baik tidak bergantung pada bentuk kedua
populasi (normal atau bukan).
• Akan tetapi, bila n1 dan n2 keduanya kurang dari 30,
hampiran normal lumayan baik kecuali bila kedua
hampiran normal lumayan baik kecuali bila kedua
populasi jauh dari normal.
• Tentu saja jika kedua populasi normal, maka
berdistribusi normal terlepas dari ukuran n1 dan n2 .
32

• Contoh 12. Suatu sampel berukuran n1=15 diambil
secara acak dari populasi yang berdistribusi normal
dengan rataan =50 dan variansi = 9, dan rataan
sampel dihitung. Sampel acak kedua berukuran
n2= 4 diambil, bebas dari yang pertama, dari populasi
lain yang juga berdistribusi normal, dengan rataan =
40 dan variansi = 4, dan rataan sampel dihitung.
40 dan variansi = 4, dan rataan sampel dihitung.
Carilah P( < 8,2).
33

Jawaban: Dari distribusi sampel kita ketahui bahwa
distribusinya normal dengan rataan dan variansi
= 50 – 40 = 10
=
Peluang yang dicari dinyatakan oleh luas daerah yang dihitami
dalam gambar. Berpadanan dengan nilai = 8,2 ,
dalam gambar. Berpadanan dengan nilai = 8,2 ,
diperoleh sehingga
P( < 8,2 ) = P (Z < -1,08)
= 0,1401
Gambar 2. Luas Daerah Untuk Contoh 12
34

• Contoh 13. tabung gambar televisi yang dibuat pabrik A
mempunyai rataan umur 6.5 tahun dengan simpangan baku
0.9 tahun, sedangkan hasil dari pabrik B mempunyai rataan
umur 6.0 tahun dengan simpangan baku 0.8 tahun. Berapakah
peluang bahwa suatu sampel acak berukuran 36 buah tabung
dari pabrik A akan mempunyai rataan umur paling sedikit satu
tahun lebih lama dari rataan umur sampel 49 buah tabung
dari pabrik B?
Jawaban: Diketahui data berikut:
Populasi I Populasi II
---------------------------------
µ1 = 6.5 µ2 = 6.0
σ1 = 0.9 σ2 = 0.8
n1 = 36 n2 = 49
35

Distribusi sampel akan berdistribusi hampiran
normal dan mempunyai rataan dan simpangan baku:
= 6.5 – 6.0 = 0.5
189
.
0
49
64
.
0
36
81
.
0
2
1
=
+
=
−X
X
σ
Peluang bahwa rataan 36 buah tabung dari pabrik A paling
sedikit 1 tahun lebih lama dari rataan 49 tabung dari pabrik B
adalah P( ≥ 1.0)
Padanan nilai 1.0 adalah z = (1.0 – 0.5)/0.189 = 2.65
Sehingga
P( ≥ 1.0) = P(Z > 2.65) = 1 – P(Z < 2.65)
= 1 – 0.9960 = 0.0040
36

• Latihan. Di sebuah universitas terdapat dua populasi,
yaitu populasi mahasiswa laki-laki dan populasi
mahasiswa perempuan. Diketahui rata-rata tinggi
badan mahasiswa laki-laki adalah 164 cm dengan
simpangan baku 5.3 cm, sedangkan rata-rata tinggi
mahasiswa perempuan adalah 153 cm dengan
simpangan baku 5.1 cm. Misalka n dari kedua
simpangan baku 5.1 cm. Misalka n dari kedua
populasi tersebut diambil sampel secara acak yang
saling bebas masing-masing 150 orang, berapa
peluang rata-rata tinggi mahasiswa laki-laki paling
sedikit 12 cm lebihnya daripada rata-rata tinggi
mahasiswa perempuan.
37

Jawaban: Diketahui data berikut:
Populasi I Populasi II
---------------------------------
µ1 = 164 µ2 = 153
σ1 = 5.3 σ2 = 5.1
n1 = 150 n2 = 150
Misalkan dan masing-masing menyatakan rata-rata
tinggi badan mahasiswa laki-laki dan rata-rata tinggi
1
X 2
X
tinggi badan mahasiswa laki-laki dan rata-rata tinggi
mahasiswa perempuan.
Karena ukuran sampel cukup besar (≥ 30), maka distribusi
sampel akan berdistribusi hampiran normal dan
mempunyai rataan dan simpangan baku:
= 164 – 158 = 11 cm
38
1 2
60
.
0
150
)
1
.
5
(
150
)
3
.
5
( 2
2
2
1
=
+
=
−X
X
σ

Peluang bahwa rata-rata tinggi mahasiswa laki-laki paling
sedikit 12 cm lebihnya daripada rata-rata tinggi mahasiswa
perempuan adalah P( ≥ 12)
Padanan nilai 12 adalah z = (12 – 11)/0.60 = 1.67
Sehingga
P( ≥ 12) = P(Z > 1.67) = 1 – P(Z < 1.67)
= 0.0475
= 0.0475
39

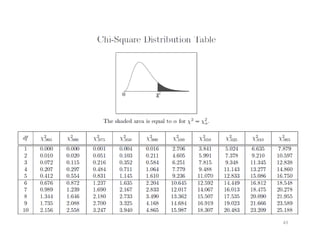
Distribusi Sampel dari (n – 1)S2/σ
σ
σ
σ2
• Teorema. Bila S2 adalah variansi sampel acak
berukuran n yang diambil dari populasi normal
dengan varians i , maka statistik
berdistribusi khi-kuadrat dengan derajat kebebasan
adalah v = n – 1.
40

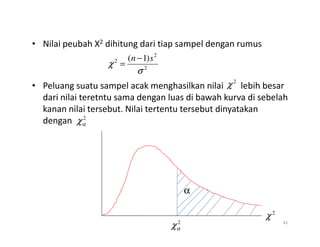
• Nilai peubah X2 dihitung dari tiap sampel dengan rumus
• Peluang suatu sampel acak menghasilkan nilai lebih besar
dari nilai teretntu sama dengan luas di bawah kurva di sebelah
kanan nilai tersebut. Nilai tertentu tersebut dinyatakan
dengan
2
2
2 )
1
(
σ
χ
s
n −
=
2
χ
2
α
χ
dengan
α
41
α
χ
2
α
χ
2
χ

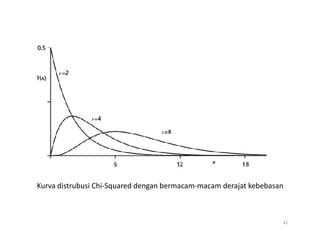
42
Kurva distrubusi Chi-Squared dengan bermacam-macam derajat kebebasan

• Contoh 14. Suatu pabrik baterai mobil menjamin
bahwa baterainya akan tahan rata-rata 3 tahun
dengan simpangan baku 1 tahun. Bila 5 baterainya
tahan 1,9, 2,4, 3,0, 3,5, dan 4,2 tahun, apakah
pembuatnya masih yakin bahwa simpangan baku
baterai tersebut 1 tahun ?
45

Jawaban:
• Mula-mula dihitung variansi sampel :
kemudian
26
.
3
1
)
815
.
0
)(
4
(
2
=
=
χ
merupakan suatu nilai distribusi khi-kuadrat dengan
derajat kebebasan 4. Karena 95% nilai dengan derajat
kebebasan 4 terletak antara 0,484 dan 11,143, nilai
perhitungan dengan menggunakan = 1 masih wajar,
sehingga tidak ada alasan bagi pembuatnya untuk
mencurigai bahwa simpangan baku baterainya bukan 1
tahun.
46
1
2
χ

Distribusi-t
• Variansi populasi yang sampel acaknya diambil
seringkali sukar diketahui.
• Untuk ukuran sampel yang besar (n ≥ 30), taksiran σ2
yang baik dapat diperoleh dengan menghitung S2.
• Untuk n yang kecil, nilai S2 berubah cukup besar dari
• Untuk n yang kecil, nilai S2 berubah cukup besar dari
sampel ke sampel lainnya dan distribusi peubah acak
Z = menyimpang cukup jauh dari
distribusi normal baku.
• Untuk sampel berukuran kecil, kita berhadapan dengan
distribusi suatu statistik yang dinamakan T.
47
)
/
/(
)
( n
X σ
µ
−

• T adalah peubah acak dengan
, yang dalam hal ini
dan distribusi peluangnya dinamakan distribusi t (akan
didefinisikan kemudian).
n
S
X
=
σ
• Distribusi t ditemukan oleh W.S Gosset pada tahun 1908
dalam sebuah makalahnya. Gosset bekerja di sebuah pabrik di
Irlandia yang melarang karyawannya menerbitkan
penelitiannya. Untuk menyiasati larangan itu, dia menerbitkan
karyanya secara rahasia dibawah nama “student”, karena
itulah distribusi t disebut distribusi student.
48

Teorema. Misalkan Z peubah acak normal baku dan V
peubah acak khi-kuadrat dengan derajat kebebasan v.
Bila Z dan V bebas, maka distribusi peubah acak T, bila
diberikan oleh
diberikan oleh
Ini dikenal dengan nama distribusi–t dengan derajat
kebebasan v.
49

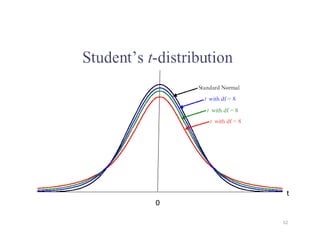
• Dalam menurunkan rumus distribusinya, Gosset
mengasumsikan bahwa sampel acak diambil dari populasi
normal.
• Meskipun demikian, bila sampel acak diambil dari sampel
yang distribusinya tidak normal tetapi bila kurva distribusinya
berbentuk lonceng, maka dapat dibuktikan bahwa distribusi
statistik tersebut masih mendekati distribusi t.
• Distribusi t sangat mirip dengan distribusi normal baku Z,
• Distribusi t sangat mirip dengan distribusi normal baku Z,
keduanya setangkup terhadap rataan 0, tetapi distribusi t
lebih bervariasi karena nilai T sangat bergantung pada
perubahan nilai dan S2, sedangkan distribusi normal hanya
bergantung pada perubahan nilai dari suatu sampel ke
sampel yang lain.
50
X
X

• Distribusi t dan Z berbeda karena variansi T bergantung pada
ukuran sampel n dan variansi ini selalu lebih besar dari 1.
Hanya jika n →∞, kedua distribusi ini akan menjadi sama.
• Perhatikan rumus variansi S2 yang terdahulu:
Faktor pembagi yang muncul, yaitu n – 1, disebut derajat
kebebasan, yang ditulis v = n – 1. Kurva distribusi t akan
bervariasi untuk berbagai derajat kebebasan. Bila n →∞,
maka v = ∞ sehingga distribusi t menjadi sama dengan
distribusi normal baku Z.
51

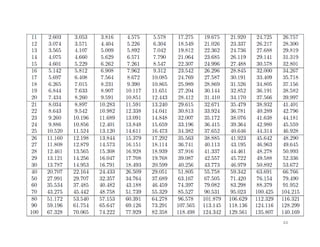
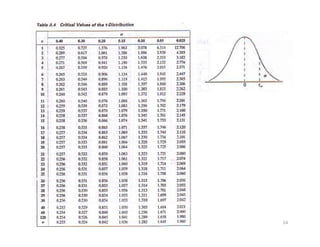
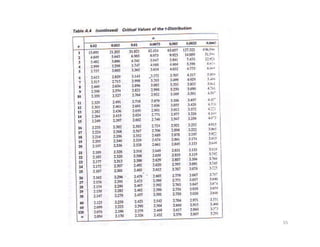
• Peluang suatu sampel acak mempunyai nilai
yang terletak antara dua nilai tertentu sama dengan luas di
bawah kurva distribusi t yang dibatasi oleh absis yang
berpadanan dengan kedua nilai tersebut.
• Perhitungan distribusi t dilakukan dengan memakai Tabel
Distribusi t. Pada tabel telah tercantum nilai-nilai t untuk
)
/
/(
)
( n
s
x
t µ
−
=
derajat kebebasan v dan luas di bawah kurva (disimbolkan
dengan α).
• Tabel tersebut memberikan nilai t sedemikian rupa sehingga
di atasnya terdapat luas α tertentu.
53

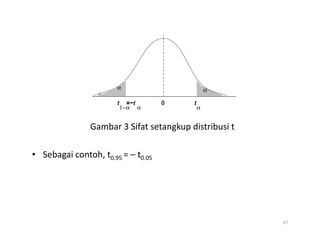
• Notasi: tα menyatakan nilai t sedemikian sehingga di sebelah
kanannya terdapat luas sebesar α
• Sebagai contoh, nilai t untuk derajat kebebasan 10 sehingga
luas bagian paling kanan 0.025 adalah 2.228, atau ditulis t0.025
= 2.228 untuk derajat kebebasan 10.
• Karena distribusi t setangkup terhadap rataan nol, maka
• Karena distribusi t setangkup terhadap rataan nol, maka
t 1 – α = – t α
yang artinya nilai t yang luas di sebelah kanannya 1 – α sama
dengan minus nilai t yang luas bagian kanannya α (lihat
Gambar 3).
56

Gambar 3 Sifat setangkup distribusi t
Gambar 3 Sifat setangkup distribusi t
• Sebagai contoh, t0.95 = – t0.05
57

• Contoh 15. Nilai t dengan derajat kebebasan v = 14 sehingga
luas di sebelah kirinya 0.025 (jadi luas di sebelah kanannya = 1
– 0.025 = 0.975) adalah
t0.975 = – t0.025 = – 2.145
• Contoh 16. Cari P(-t0,025 T t0,05).
Jawaban :
Karena luas di sebelah kanan t adalah 0,05 dan luas di
Karena luas di sebelah kanan t0,05 adalah 0,05 dan luas di
sebelah kiri -t0,025 adalah 0,025, maka jumlah luas antara -t0,025
dan t0,05 adalah
1 – 0,05 – 0,025 = 0,925
jadi P(-t0,025 T t0,05) = 0,925
58

• Contoh 17. Untuk sampel berukuran n = 10 dan α = 0.05,
tentukanlah P(T t α) dan P(- t α T t α ).
Jawaban: Derajat kebebasan = n – 1 = 10 – 1 = 9.
t 0.05 = 1.833
Jadi, P(T 1.833) = 1 – 0.05 = 0.95
dan P(-1.833 T 1.833) = 1 – 0.05 – 0.05 = 0.90
59

• Perhatikan bahwa 95% dari nilai peluang suatu
distribusi t dengan derajat kebebasan v = n – 1
berada antara –t0,025 dan t0,025
• Suatu nilai t yang jatuh di bawah –t0,025 dan t0,025
akan cenderung memberi keyakinan pada kita bahwa
suatu kejadian yang amat jarang terjadi telah terjadi
atau anggapan kita mengenai µ yang kita ambil
atau anggapan kita mengenai µ yang kita ambil
keliru.
• Jika hal ini muncul maka kita akan memilih
kesimpulan yang terakhir dan menyatakan bahwa
anggapan nilai µ yang kita ambil keliru.
60

• Contoh 18. Sebuah pabrik lampu yakin bahwa bola lampunya
akan terus menyala selama 500 jam. Untuk mempertahankan
nilai tersebut, tiap bulan diuji 25 bola lampu. Bila nilai t yang
dihitung terletak antara –t0,05 dan t0,05 maka pengusaha
pabrik tadi akan mempertahankan keyakinannya. Kesimpulan
apakah yang seharusnya dia ambil dari sampel dengan rataan
518 jam dan simpangan baku 40 jam? Anggaplah bahwa
distribusi waktu menyala, secara hampiran, normal.
Jawaban:
Derajat kebebasan = 25 – 1 = 24
Dari tabel t diperoleh t0,05 = 1.711 .
Jadi pengusaha tadi akan puas dengan keyakinannya bila
sampel 25 lampu memberikan nilai t antara –1.711 dan
1.711
61

Bila µ = 500, maka
t =
suatu nilai yang jauh dari 1.711 . Jadi pengusaha tadi tidak
yakin karena 2.25 1.711.
25
.
2
25
/
40
500
518
=
−
62

Distribusi-F
Statistik F didefinisikan sebagai nisbah dua peubah
acak khi-kuadrat yang bebas, masing-masing dibagi
dengan derajat kebebasannya.
Jadi dapat ditulis
U dan V : peubah acak bebas.
v1 dan v2 : derajat kebebasan.
63

Teorema. Misalkan U dan V dua peubah acak
bebas masing-masing berdistribusi khi-kuadrat
dengan derajat kebebasan v1 dan v2. Maka
distribusi peubah acak
diberikan oleh
diberikan oleh
Ini dikenal dengan nama distribusi–F dengan
derajat kebebasan v1 danv2.
64

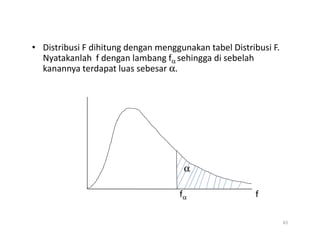
• Distribusi F dihitung dengan menggunakan tabel Distribusi F.
Nyatakanlah f dengan lambang fα sehingga di sebelah
kanannya terdapat luas sebesar α.
α
fα f
65

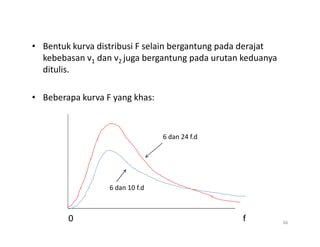
• Bentuk kurva distribusi F selain bergantung pada derajat
kebebasan v1 dan v2 juga bergantung pada urutan keduanya
ditulis.
• Beberapa kurva F yang khas:
66
6 dan 10 f.d
6 dan 24 f.d
f
0

• Contoh 19. Untuk suatu distribusi–F hitunglah f0,05 bila v1 = 6
dan v2 = 10.
Jawaban : Dengan menggunakan Tabel F, diperoleh
f0,05 = 3,22
• Jika diketahui fα kita dapat menghitung f1- α dengan teorema
berikut
berikut
• Teorema. Tuliskan fα(v1, v2) untuk fα dengan derajat
kebebasan v1 dan v2, maka
67
)
,
(
1
)
,
(
1
2
2
1
1
v
v
f
v
v
f
α
α =
−

• Contoh 20. Hitunglah nilai f dengan derajat kebebasan 6 dan
10 sehingga luas sebelah kanannya 0.95.
Jawaban:
246
.
0
06
.
4
1
)
6
,
10
(
1
)
10
,
6
(
05
.
0
95
.
0 =
=
=
f
f
68

Teorema. Bila dan adalah variansi
sampel acak yang bebas berukuran n1 dan
n2 yang diambil dari dua populasi
berdistribusi–F dengan derajat kebebasan v1
= n1 - 1 dan v2 = n2 - 2
69

�ݺ�ߣ

Materi Matematika: Sampel Acak dan Distribusinya

More Related Content

Similar to Materi Matematika: Sampel Acak dan Distribusinya (20)

Recently uploaded (20)

Materi Matematika: Sampel Acak dan Distribusinya