Material didÃĄctico differential calculus
8 likes1,089 views
A function is a relationship where one quantity depends on another. The area of a circle is a function of its radius, as the area changes when the radius changes. Derivatives show the rate of change of a function at a point and represent an infinitesimal change in the function with respect to one of its variables. Optimization problems aim to find the maximum or minimum value of a function subject to constraints.
1 of 14
Downloaded 50 times



Ad
Recommended
Computed Prediction: So far, so good. What now?
Computed Prediction: So far, so good. What now?Xavier LlorÃ
Ėý
This document discusses computed prediction in learning classifier systems (LCS). It addresses representing the payoff function Q(s,a) that maps state-action pairs to expected future payoffs. Specifically:
1) In computed prediction, each classifier has parameters w and the classifier prediction is computed as a parametrized function p(x,w) like a linear approximation.
2) Classifier weights are updated using the Widrow-Hoff rule online as the payoff function is learned.
3) Using a powerful approximator like tile coding to compute predictions allows the problem to potentially be solved by a single classifier, but evolution of different approximators per problem subspace may stillSite visit presentation 2012 12 14
Site visit presentation 2012 12 14Mitchell Wand
Ėý
This document summarizes Mitchell Wand's presentation on providing static guarantees for macro bindings. It discusses the motivation for studying macros and desire for static reasoning about hygiene. While previous work addressed related problems dynamically, the goal here is to provide static guarantees. The presentation outlines previous work and the starting points being built upon, including Ott specification language and Herman's thesis. It describes progress made in adapting Pottier's Functional Fresh ML to use plain s-expressions while keeping binding information in types. Next steps include interfacing with an SMT prover and implementing example macros in the system.Definitions of Functional Programming
Definitions of Functional ProgrammingPhilip Schwarz
Ėý
The document discusses definitions of functional programming from multiple sources. Functional programming is defined as programming using only pure functions and immutable values. A pure function is one that depends solely on its input parameters and algorithm to produce output, without side effects like modifying external state or performing I/O. Pure functions have properties of being total, deterministic, and inculpable/having no side effects. Functional programming involves writing programs as compositions of pure functions.Value of a polynomial function(check)
Value of a polynomial function(check)JohnMichael0406
Ėý
A polynomial function is a mathematical expression involving the sum of terms, each of which is a constant multiplied by one or more variables raised to a non-negative integer power. The value of a polynomial function can be determined by substituting specific numbers for the variables and evaluating the resulting expression. Polynomial functions are widely used in science, engineering, and other fields to model real-world relationships between variables.Derivativedemo
DerivativedemoPaul Roundy
Ėý
This document introduces basic differential calculus concepts focused on slopes of lines, specifically using the equation y=mx+b. It illustrates the relationship between a curve, such as y=-x^2, and its slope, leading to the understanding that the derivative at any point is -2 times the x-value at that point. The document encourages practicing similar steps with other functions like y=x^3 to solidify comprehension of calculus principles.maths ppt
maths ppt Abhinav Saxena
Ėý
The document provides brief biographies of famous mathematicians including Aryabhata, Pythagoras, Euclid, Gauss, Fourier, Cauchy, Galois, Riemann, Einstein, Descartes, and Devi. It also discusses what mathematics is and defines a mathematician as someone who uses extensive mathematical knowledge to solve problems.Lesson 16: Derivatives of Exponential and Logarithmic Functions
Lesson 16: Derivatives of Exponential and Logarithmic FunctionsMatthew Leingang
Ėý
The document discusses the derivatives of exponential and logarithmic functions, detailing how to calculate them for the natural exponential function and the natural logarithm. It explains concepts like exponential growth, logarithmic differentiation, and provides examples of finding derivatives for various functions. Key formulas and theorems related to these topics are also highlighted.ppt of Calculus
ppt of CalculusNirali Akabari
Ėý
The document discusses concepts related to calculus including tangent planes, normal lines, and linear approximations. It provides definitions and equations for calculating the tangent plane to a surface, the normal line to a curve or surface, and using the tangent line as a linear approximation near a given point on a function. Examples are given to demonstrate finding the total derivative of a function and using the tangent line as a linearization.Math major 14 differential calculus pw
Math major 14 differential calculus pwReymart Bargamento
Ėý
This document provides an overview of topics covered in a differential calculus course, including:
1. Limits and differential calculus concepts such as derivatives
2. Special functions and numbers used in calculus
3. A brief history of calculus and its founders Newton and Leibniz
4. Explanations and examples of key calculus concepts such as variables, constants, functions, and limitsCalculus
Calculusezhilcharu
Ėý
This document discusses integral and differential calculus and their applications. It covers the fundamental theorems of calculus, how calculus helps understand space, time and motion, and how it provides tools to resolve paradoxes. It also notes that calculus is used in physics, chemistry, engineering, economics, medicine and other fields, and can find optimal solutions and approximate equations. It encourages learning more about calculus.Differential calculus
Differential calculusJuan Apolinario Reyes
Ėý
This problem set covers differential calculus and requires students to find the derivatives of given functions and solve the equation 2=x+e-x. Students are instructed to write their solutions neatly and orderly.A Course of Calculus for IT-Students
A Course of Calculus for IT-Studentsmetamath
Ėý
This document outlines a course of calculus for IT students at Lobachevsky State University of Nizhni Novgorod. The course is divided into 3 terms covering sequences, differential calculus, integral calculus, and series. Tests and exams are given throughout each term to assess student competency in mathematical thinking and problem solving. The course aims to develop skills in applying modern mathematical tools. Plans are discussed to modernize the course by adding an introductory section to address low student preparation, using online tools like METAMATH to support independent work, and testing key concepts to address educational problems.Integral calculus
Integral calculusFarzad Javidanrad
Ėý
1) The document discusses basic rules and concepts of integration, including that integration is the inverse process of differentiation and that the indefinite integral of a function f(x) is notated as âŦf(x) dx = F(x) + c, where F(x) is the primitive function and c is the constant of integration.
2) Methods of integration discussed include the substitution method, where a function is substituted for the variable, and integration by parts, which uses the product rule in reverse to solve integrals involving products.
3) Finding the constant of integration c requires knowing the value of the primitive function F(x) at a specific point, which eliminates the family of functions and isolates aCalculus Ppt
Calculus Pptguest5d26f0c
Ėý
Trigonometric functions are used extensively in calculus. When using trig functions in calculus, radian measure must be used for angles. Even trig functions like cosine are symmetric about the y-axis, while odd functions like sine change sign when x changes sign. Trig functions can be shifted, stretched, or shrunk by applying transformations to their graphs.Integral Calculus
Integral Calculusitutor
Ėý
This document discusses integration, which is the inverse process of differentiation. Integration allows us to find the original function given its derivative. Several integration techniques are explained, including substitution, integration by parts, and finding volumes of revolution. Standard integrals are presented along with examples of calculating areas under curves and volumes obtained by rotating areas about axes. Definite integrals are used to find the area between curves over a specified interval.The Application of Derivatives
The Application of Derivativesdivaprincess09
Ėý
This document discusses several topics related to calculus including:
1) Derivatives of position, velocity, and acceleration and how they relate to each other.
2) An example problem calculating velocity from a position function.
3) The Mean Value Theorem and how to apply it to find critical points of a function.
4) How the first and second derivatives of a function relate to critical points, maxima, minima, and points of inflection or concavity.
5) Related rates problems and how to set them up using derivatives and relationships between variables.Application of calculus in everyday life
Application of calculus in everyday lifeMohamed Ibrahim
Ėý
The document discusses Newton's Law of Cooling and its applications through differential equations.
- Newton's Law of Cooling states that the rate of change of an object's temperature is proportional to the difference between the object's temperature and the ambient temperature. This can be modeled as a first-order differential equation.
- The equation can be derived and solved using calculus techniques like separation of variables. The solution is an exponential decay function.
- Real-world applications include determining time of death from body temperature, designing efficient cooling systems for computer processors, and calculating heat transfer rates in devices like solar water heaters. Mathematical problems demonstrate using the law of cooling in investigations and engineering design.Applications of Derivatives
Applications of DerivativesIram Khan
Ėý
The document is a project on derivatives, discussing their definition, history, real-life applications, and significance in various sciences. It covers the fundamentals of derivatives, their applications in physics, biology, economics, and other fields, and emphasizes their relevance in daily life. The conclusion highlights the importance of understanding derivatives for various professions.Calculus in real life
Calculus in real lifeSamiul Ehsan
Ėý
Calculus has many applications in real life. It is used in fields like engineering, biology, science, economics and other areas. In engineering, calculus is used for building structures like skyscrapers and bridges and in robotics for determining how robotic parts will move with commands. It is also used in electrical and computer engineering for system design. In biology, calculus is applied to study ecosystem interactions and model drug concentrations in organisms. It also measures growth rates. Astronomy and space technology heavily rely on calculus. Economics uses calculus for functions, derivatives, and finding optimal solutions. Doctors and mapping also apply calculus. In summary, calculus has diverse real-world uses across many domains due to its ability to modelLimits and continuity powerpoint
Limits and continuity powerpointcanalculus
Ėý
The document discusses limits and continuity, explaining what limits are, how to evaluate different types of limits using techniques like direct substitution, dividing out, and rationalizing, and how limits relate to concepts like derivatives, continuity, discontinuities, and the intermediate value theorem. Special trig limits, properties of limits, and how limits can be used to find derivatives are also covered.Limits and derivatives
Limits and derivativesLaxmikant Deshmukh
Ėý
The document discusses functions and their derivatives. It defines functions, different types of functions, and notation used for functions. It then covers the concept of limits, theorems on limits, and limits at infinity. The document defines the slope of a tangent line to a curve and increments. It provides definitions and rules for derivatives, including differentiation from first principles and various differentiation rules. It includes examples of finding derivatives using these rules and taking multiple derivatives.AP Advantage: AP Calculus
AP Advantage: AP CalculusShashank Patil
Ėý
The document provides an overview of the structure and content covered on the AP Calculus AB exam, including:
- The exam is 3 hours 15 minutes long and divided into multiple choice and free response sections testing limits, derivatives, integrals, and applications of calculus.
- Content topics covered include limits of functions, continuity, derivatives and their applications (related rates, max/min problems), integrals, and differential equations.
- Formulas and strategies are provided for evaluating limits, finding derivatives using various rules, applying derivatives to sketch curves, solve optimization problems, and solve motion problems using related rates.0.5.derivatives
0.5.derivativesm2699
Ėý
The document outlines key calculus concepts including:
- Functions, derivatives, differentiation rules, and the definition of a derivative as an infinitesimal change in a function with respect to a variable.
- Concepts related to derivatives such as local/absolute extrema, critical points, increasing/decreasing functions, concavity, asymptotes, and inflection points.
- How to use the first and second derivative tests to determine local extrema, concavity, and increasing/decreasing behavior.Functions and Limits
Functions and LimitsLesterTubo
Ėý
This document defines key terms related to functions, limits, and graphs. It explains that a domain is the set of input values for a function, while the range is the set of possible output values. A function assigns each input a single output. Limits describe the behavior of a function as the input approaches a value, without reaching it. Examples demonstrate evaluating limits of various polynomial functions as the variable approaches a value.Calculus BC
Calculus BCSpandana Govindgari
Ėý
This document provides an overview of key concepts in calculus, including limits, derivatives, integrals, and their applications. It defines limits, derivatives, and integrals, outlines techniques for evaluating them, and describes how to analyze functions using derivatives and integrals. Key topics covered include finding limits analytically and graphically, the definition of the derivative, rules for derivatives of common functions, antidifferentiation, Riemann sums, the Mean Value Theorem, and improper integrals.Calculus- Basics
Calculus- BasicsRabin BK
Ėý
The document is an educational presentation on calculus and analytical geometry covering key concepts such as relations, functions, limits, continuity, derivatives, and their applications. It explains the definitions of one-to-one, onto, and composite functions, as well as types of limits and discontinuities. Additionally, it discusses the application of derivatives for curve sketching, including criteria for local maxima and minima.Function
Function QamarAbbasJaffari
Ėý
This document contains a summary of key concepts in mathematics functions including:
- Definitions of different types of functions such as polynomial, rational, trigonometric, exponential, and logarithmic functions.
- Concepts related to functions like domain, range, and notation for functions.
- Examples demonstrating how to find the domain and range of functions.
- Key topics in trigonometry including trigonometric functions, trigonometric tables, addition formulas, laws of sines and cosines.
- Concepts of limits, average and instantaneous rates of change, techniques for finding limits, and limits involving infinity.267 handout 2_partial_derivatives_v2.60
267 handout 2_partial_derivatives_v2.60Ali Adeel
Ėý
This document provides an overview of partial derivatives, which are used to analyze functions with multiple variables. Key topics covered include:
- Definitions of limits, continuity, and partial derivatives for multivariable functions.
- Directional derivatives and the gradient, which describe the rate of change in a specified direction.
- The chain rule for partial derivatives, and implicit differentiation.
- Linearization and Taylor series approximations for multivariable functions.
- Finding local extrema and optimizing functions, using techniques like classifying critical points.DIFFERENTIAL CALCULUS AND TRIGONOMETRY Dharani.pptx
DIFFERENTIAL CALCULUS AND TRIGONOMETRY Dharani.pptxDHARANI A
Ėý
The document introduces concepts of differential calculus and trigonometric functions, defining functions as ordered pairs and explaining their domains and ranges. It covers limits, techniques for evaluating limits, and the role of derivatives in determining increasing and decreasing functions. Additionally, it addresses maximum/minimum problems in calculus, including a specific example related to optimizing the surface area of a box given a fixed volume.More Related Content
Viewers also liked (11)
Math major 14 differential calculus pw
Math major 14 differential calculus pwReymart Bargamento
Ėý
This document provides an overview of topics covered in a differential calculus course, including:
1. Limits and differential calculus concepts such as derivatives
2. Special functions and numbers used in calculus
3. A brief history of calculus and its founders Newton and Leibniz
4. Explanations and examples of key calculus concepts such as variables, constants, functions, and limitsCalculus
Calculusezhilcharu
Ėý
This document discusses integral and differential calculus and their applications. It covers the fundamental theorems of calculus, how calculus helps understand space, time and motion, and how it provides tools to resolve paradoxes. It also notes that calculus is used in physics, chemistry, engineering, economics, medicine and other fields, and can find optimal solutions and approximate equations. It encourages learning more about calculus.Differential calculus
Differential calculusJuan Apolinario Reyes
Ėý
This problem set covers differential calculus and requires students to find the derivatives of given functions and solve the equation 2=x+e-x. Students are instructed to write their solutions neatly and orderly.A Course of Calculus for IT-Students
A Course of Calculus for IT-Studentsmetamath
Ėý
This document outlines a course of calculus for IT students at Lobachevsky State University of Nizhni Novgorod. The course is divided into 3 terms covering sequences, differential calculus, integral calculus, and series. Tests and exams are given throughout each term to assess student competency in mathematical thinking and problem solving. The course aims to develop skills in applying modern mathematical tools. Plans are discussed to modernize the course by adding an introductory section to address low student preparation, using online tools like METAMATH to support independent work, and testing key concepts to address educational problems.Integral calculus
Integral calculusFarzad Javidanrad
Ėý
1) The document discusses basic rules and concepts of integration, including that integration is the inverse process of differentiation and that the indefinite integral of a function f(x) is notated as âŦf(x) dx = F(x) + c, where F(x) is the primitive function and c is the constant of integration.
2) Methods of integration discussed include the substitution method, where a function is substituted for the variable, and integration by parts, which uses the product rule in reverse to solve integrals involving products.
3) Finding the constant of integration c requires knowing the value of the primitive function F(x) at a specific point, which eliminates the family of functions and isolates aCalculus Ppt
Calculus Pptguest5d26f0c
Ėý
Trigonometric functions are used extensively in calculus. When using trig functions in calculus, radian measure must be used for angles. Even trig functions like cosine are symmetric about the y-axis, while odd functions like sine change sign when x changes sign. Trig functions can be shifted, stretched, or shrunk by applying transformations to their graphs.Integral Calculus
Integral Calculusitutor
Ėý
This document discusses integration, which is the inverse process of differentiation. Integration allows us to find the original function given its derivative. Several integration techniques are explained, including substitution, integration by parts, and finding volumes of revolution. Standard integrals are presented along with examples of calculating areas under curves and volumes obtained by rotating areas about axes. Definite integrals are used to find the area between curves over a specified interval.The Application of Derivatives
The Application of Derivativesdivaprincess09
Ėý
This document discusses several topics related to calculus including:
1) Derivatives of position, velocity, and acceleration and how they relate to each other.
2) An example problem calculating velocity from a position function.
3) The Mean Value Theorem and how to apply it to find critical points of a function.
4) How the first and second derivatives of a function relate to critical points, maxima, minima, and points of inflection or concavity.
5) Related rates problems and how to set them up using derivatives and relationships between variables.Application of calculus in everyday life
Application of calculus in everyday lifeMohamed Ibrahim
Ėý
The document discusses Newton's Law of Cooling and its applications through differential equations.
- Newton's Law of Cooling states that the rate of change of an object's temperature is proportional to the difference between the object's temperature and the ambient temperature. This can be modeled as a first-order differential equation.
- The equation can be derived and solved using calculus techniques like separation of variables. The solution is an exponential decay function.
- Real-world applications include determining time of death from body temperature, designing efficient cooling systems for computer processors, and calculating heat transfer rates in devices like solar water heaters. Mathematical problems demonstrate using the law of cooling in investigations and engineering design.Applications of Derivatives
Applications of DerivativesIram Khan
Ėý
The document is a project on derivatives, discussing their definition, history, real-life applications, and significance in various sciences. It covers the fundamentals of derivatives, their applications in physics, biology, economics, and other fields, and emphasizes their relevance in daily life. The conclusion highlights the importance of understanding derivatives for various professions.Calculus in real life
Calculus in real lifeSamiul Ehsan
Ėý
Calculus has many applications in real life. It is used in fields like engineering, biology, science, economics and other areas. In engineering, calculus is used for building structures like skyscrapers and bridges and in robotics for determining how robotic parts will move with commands. It is also used in electrical and computer engineering for system design. In biology, calculus is applied to study ecosystem interactions and model drug concentrations in organisms. It also measures growth rates. Astronomy and space technology heavily rely on calculus. Economics uses calculus for functions, derivatives, and finding optimal solutions. Doctors and mapping also apply calculus. In summary, calculus has diverse real-world uses across many domains due to its ability to modelSimilar to Material didÃĄctico differential calculus (20)
Limits and continuity powerpoint
Limits and continuity powerpointcanalculus
Ėý
The document discusses limits and continuity, explaining what limits are, how to evaluate different types of limits using techniques like direct substitution, dividing out, and rationalizing, and how limits relate to concepts like derivatives, continuity, discontinuities, and the intermediate value theorem. Special trig limits, properties of limits, and how limits can be used to find derivatives are also covered.Limits and derivatives
Limits and derivativesLaxmikant Deshmukh
Ėý
The document discusses functions and their derivatives. It defines functions, different types of functions, and notation used for functions. It then covers the concept of limits, theorems on limits, and limits at infinity. The document defines the slope of a tangent line to a curve and increments. It provides definitions and rules for derivatives, including differentiation from first principles and various differentiation rules. It includes examples of finding derivatives using these rules and taking multiple derivatives.AP Advantage: AP Calculus
AP Advantage: AP CalculusShashank Patil
Ėý
The document provides an overview of the structure and content covered on the AP Calculus AB exam, including:
- The exam is 3 hours 15 minutes long and divided into multiple choice and free response sections testing limits, derivatives, integrals, and applications of calculus.
- Content topics covered include limits of functions, continuity, derivatives and their applications (related rates, max/min problems), integrals, and differential equations.
- Formulas and strategies are provided for evaluating limits, finding derivatives using various rules, applying derivatives to sketch curves, solve optimization problems, and solve motion problems using related rates.0.5.derivatives
0.5.derivativesm2699
Ėý
The document outlines key calculus concepts including:
- Functions, derivatives, differentiation rules, and the definition of a derivative as an infinitesimal change in a function with respect to a variable.
- Concepts related to derivatives such as local/absolute extrema, critical points, increasing/decreasing functions, concavity, asymptotes, and inflection points.
- How to use the first and second derivative tests to determine local extrema, concavity, and increasing/decreasing behavior.Functions and Limits
Functions and LimitsLesterTubo
Ėý
This document defines key terms related to functions, limits, and graphs. It explains that a domain is the set of input values for a function, while the range is the set of possible output values. A function assigns each input a single output. Limits describe the behavior of a function as the input approaches a value, without reaching it. Examples demonstrate evaluating limits of various polynomial functions as the variable approaches a value.Calculus BC
Calculus BCSpandana Govindgari
Ėý
This document provides an overview of key concepts in calculus, including limits, derivatives, integrals, and their applications. It defines limits, derivatives, and integrals, outlines techniques for evaluating them, and describes how to analyze functions using derivatives and integrals. Key topics covered include finding limits analytically and graphically, the definition of the derivative, rules for derivatives of common functions, antidifferentiation, Riemann sums, the Mean Value Theorem, and improper integrals.Calculus- Basics
Calculus- BasicsRabin BK
Ėý
The document is an educational presentation on calculus and analytical geometry covering key concepts such as relations, functions, limits, continuity, derivatives, and their applications. It explains the definitions of one-to-one, onto, and composite functions, as well as types of limits and discontinuities. Additionally, it discusses the application of derivatives for curve sketching, including criteria for local maxima and minima.Function
Function QamarAbbasJaffari
Ėý
This document contains a summary of key concepts in mathematics functions including:
- Definitions of different types of functions such as polynomial, rational, trigonometric, exponential, and logarithmic functions.
- Concepts related to functions like domain, range, and notation for functions.
- Examples demonstrating how to find the domain and range of functions.
- Key topics in trigonometry including trigonometric functions, trigonometric tables, addition formulas, laws of sines and cosines.
- Concepts of limits, average and instantaneous rates of change, techniques for finding limits, and limits involving infinity.267 handout 2_partial_derivatives_v2.60
267 handout 2_partial_derivatives_v2.60Ali Adeel
Ėý
This document provides an overview of partial derivatives, which are used to analyze functions with multiple variables. Key topics covered include:
- Definitions of limits, continuity, and partial derivatives for multivariable functions.
- Directional derivatives and the gradient, which describe the rate of change in a specified direction.
- The chain rule for partial derivatives, and implicit differentiation.
- Linearization and Taylor series approximations for multivariable functions.
- Finding local extrema and optimizing functions, using techniques like classifying critical points.DIFFERENTIAL CALCULUS AND TRIGONOMETRY Dharani.pptx
DIFFERENTIAL CALCULUS AND TRIGONOMETRY Dharani.pptxDHARANI A
Ėý
The document introduces concepts of differential calculus and trigonometric functions, defining functions as ordered pairs and explaining their domains and ranges. It covers limits, techniques for evaluating limits, and the role of derivatives in determining increasing and decreasing functions. Additionally, it addresses maximum/minimum problems in calculus, including a specific example related to optimizing the surface area of a box given a fixed volume.2.5 computations of derivatives
2.5 computations of derivativesmath265
Ėý
The document discusses properties of derivatives and how they relate to limits. It states that the sum, difference, and constant multiple rules for limits directly apply to differentiation. However, the product and quotient rules for limits do not directly apply to differentiation, which has more complicated product and quotient rules. Elementary functions are defined in terms of a few basic formulas and operations. The document then examines the sum and constant multiple rules for derivatives in more detail, proving them using limits. It also provides a geometric illustration of how the derivative of a sum is equal to the sum of the derivatives.Bahan presentasi
Bahan presentasiAngga Dimension
Ėý
This document outlines the topics to be covered in a presentation on limits, continuity, and differential calculus. It will include: graphical and numerical interpretations of limits; notation and examples of one-sided limits; evaluating limits; the relationship between limits and continuous functions; types of discontinuities; difference equations; the definition of a derivative; the relationship between limits and differentials; properties and techniques for finding derivatives of various functions like using the chain rule; higher-order derivatives; and applications of derivatives like finding maxima and minima, and analyzing monotonicity, elasticities, marginal costs, revenues, and profits.Calculus I basic concepts
Calculus I basic conceptsMontserrat Castellanos
Ėý
This document discusses key concepts in calculus including differentiation, integration, graphing functions, and calculating total vs net distance. It defines the derivative as the rate of change of a variable and outlines differentiation rules. Integration is defined as the area under a curve and the fundamental theorem of calculus is explained. Graphing techniques are outlined including finding zeros, critical points, concavity, and inflection points. Total distance is defined as the absolute distance traveled regardless of path while net distance is the displacement from the original position.Lesson 8: Basic Differentiation Rules
Lesson 8: Basic Differentiation RulesMatthew Leingang
Ėý
The document outlines the basic differentiation rules in calculus, including the power rule, sum rule, and derivatives of sine and cosine functions. It provides detailed examples of calculating derivatives for functions such as f(x) = xÂē, f(x) = xÂģ, and f(x) = âx, along with explanations of the first and second derivatives. It also discusses the concept of differentiability and includes relevant notations.Lecture co3 math21-1
Lecture co3 math21-1Lawrence De Vera
Ėý
This document discusses concepts related to calculus including limits, continuity, and derivatives of functions. Specifically, it covers:
- Definitions and theorems related to limits, continuity, and derivatives of algebraic functions.
- Evaluating limits, determining continuity of functions, and taking derivatives of algebraic functions using basic theorems of differentiation.
- The objective is for students to be able to evaluate limits, determine continuity, and find derivatives of continuous algebraic functions in explicit or implicit form after discussing these calculus concepts.Lesson 8: Basic Differentation Rules (slides)
Lesson 8: Basic Differentation Rules (slides)Mel Anthony Pepito
Ėý
This document provides an outline for a calculus lecture on basic differentiation rules. It includes objectives to understand the derivative of constants, the constant multiple rule, the sum rule, the difference rule, and derivatives of sine and cosine. Examples are provided to find the derivatives of squaring, cubing, square root, and cube root functions using the definition of the derivative. Graphs and properties of these functions and their derivatives are also discussed.Lesson 8: Basic Differentation Rules (slides)
Lesson 8: Basic Differentation Rules (slides)Matthew Leingang
Ėý
This document provides an outline for a calculus lecture on basic differentiation rules. It includes objectives to understand key rules like the constant multiple rule, sum rule, and derivatives of sine and cosine. Examples are worked through to find the derivatives of functions like squaring, cubing, square root, and cube root using the definition of the derivative. Graphs and properties of derived functions are also discussed.Inverse Functions
Inverse FunctionsAlexander Burt
Ėý
The document discusses derivatives of functions and inverse functions. It defines a function and inverse function, and explains that a function must be one-to-one to have an inverse. It also states that the slope of the tangent line to the inverse function at a point (a,b) is the inverse of the slope of the tangent line to the original function at the same point (b,a).Ad
Material didÃĄctico differential calculus
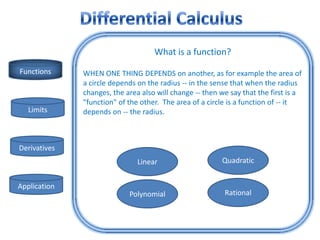
- 1. What is a function? Functions WHEN ONE THING DEPENDS on another, as for example the area of a circle depends on the radius -- in the sense that when the radius changes, the area also will change -- then we say that the first is a "function" of the other. The area of a circle is a function of -- it Limits depends on -- the radius. Derivatives Linear Quadratic Application Polynomial Rational
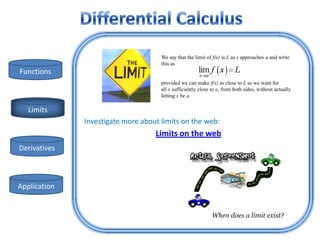
- 2. We say that the limit of f(x) is L as x approaches a and write this as Functions provided we can make f(x) as close to L as we want for all x sufficiently close to a, from both sides, without actually letting x be a. Limits Investigate more about limits on the web: Limits on the web Derivatives Application
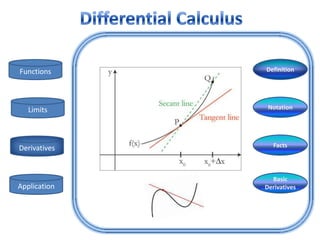
- 3. Functions Definition Limits Notation Derivatives Facts Basic Application Derivatives
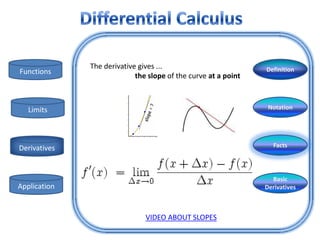
- 4. Derivatives are all about change ... ... they show how fast something is changing (called Functions the rate of change) at any point. Definition Limits Notation Derivatives The derivative of a function represents an Facts infinitesimal change in the function with respect to one of its variables. Basic Application The derivative of the function f(x) at the point is Derivatives given and denoted by:
- 5. The derivative gives ... Definition Functions the slope of the curve at a point Limits Notation Derivatives Facts Basic Application Derivatives VIDEO ABOUT SLOPES
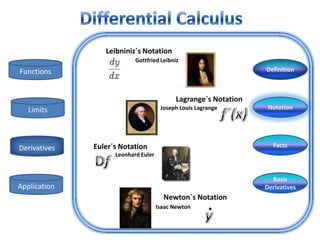
- 6. LeibninizÂīs Notation Gottfried Leibniz Functions Definition LagrangeÂīs Notation Limits Joseph Louis Lagrange Notation Derivatives EulerÂīs Notation Facts Leonhard Euler Basic Application Derivatives NewtonÂīs Notation Isaac Newton
- 7. Functions Definition Limits Notation Derivatives Facts Basic Application Derivatives
- 8. Functions Limits Derivatives Application Graphs Optimization
- 9. Linear Function Functions Limits Derivatives Linear Quadratic Application Polynomial Rational
- 10. Quadratic Function Functions Limits Derivatives Linear Quadratic Application Polynomial Rational
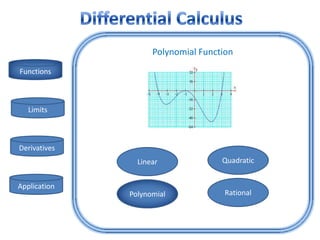
- 11. Polynomial Function Functions Limits Derivatives Linear Quadratic Application Polynomial Rational
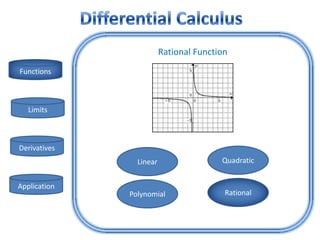
- 12. Rational Function Functions Limits Derivatives Linear Quadratic Application Polynomial Rational
- 13. One of the most Video: How to graph a Functions important uses of calculus function using is determining minimum Differential Calculus and maximum values. This has its applications in Limits manufacturing, finance, engineering, and a host of other industries. Before we examine a real-world Derivatives example, we should learn how to calculate such values. Application Graphs Optimization
- 14. In optimization problems we are looking for the largest value or the smallest value that a function can take. Here we will be Functions looking for the largest or smallest value of a function subject to some kind of constraint. The constraint will be some condition (that can usually be described by some equation) that must absolutely, positively be true no matter what our solution is. Limits Derivatives Application Graphs Optimization
