Math Common Core State Standards
- 1. Michelle L. Williams East Feliciana Parish Schools
- 2. ’üĮ Include only items that measure content common to the current grade-level expectations (GLEs) and the Common Core State Standards (CCSS) ’üĮ Content coverage will narrow to more closely match the CCSS focus areas. ’üĮ Level of test difficulty will be comparable to current tests. ’üĮ ŌĆ£Cut scoresŌĆØ will remain the same. ’üĮ New CCSS content will not be added until 2014-2015
- 3. ’üĮ Math tests will include only items that measure content common to the current grade-level expectations (GLEs) and the CCSS. ’üĮ Grades 3, 5, 6, and 7 iLEAP : To better align with CCSS, the math tests will no longer include the Iowa Test of Basic Skills (ITBS). ’üĮ Grades 4 and 8 LEAP: The math tests will be grade- level specific, rather than grade-span assessments. ’üĮ Content coverage will narrow to more closely match the CCSS focus areas.
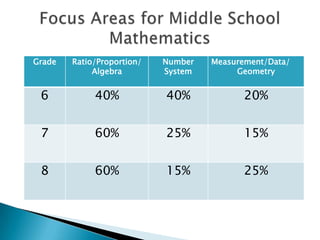
- 4. Grade Ratio/Proportion/ Number Measurement/Data/ Algebra System Geometry 6 40% 40% 20% 7 60% 25% 15% 8 60% 15% 25%
- 5. Content Area Expressions Linear Functions Number and Relationships System, Equations Measurement, and Data Algebra 20% 25% 35% 20% Geometry Proportion/ Measurement /Data Algebra Geometry 60% 25% 15%
- 6. English Language Social Grade Level Arts Mathematics Science Studies 6th 2 2 1 1 7th 2 2 1 1 8th 2 2 1 1
- 7. ACT Average EOC Graduation Index Cohort Graduation 25% 25% 25% 25%
- 8. 2012-2013 Concerns CCSS Teach from the CCSS ŌĆó Gaps in student learning 1. Grades 6-12 ŌĆóRigor 2. Class of 13ŌĆÖ & 14ŌĆÖ will not be ŌĆóStudent background knowledge effected by full implementation ŌĆóMaterials 3. Teachers will have 2 years to ŌĆóActivities prepare for full implementation ŌĆóCurriculum Maps
- 9. ’üĮ Vertical alignment of curriculum is planning curriculum across the grade levels, from Kindergarten through high school, building upon instruction based upon standards. ’üĮ Correct vertical curriculum alignment improves student performance by decreasing the amount of instructional time consumed with re-teaching concepts
- 10. ŌĆó A strong foundation K-5, students are provided hands on learning in geometry, algebra and probability and statistics. Students who have completed 7th grade and mastered the content K-5 and skills through the 7th grade will be well-prepared for algebra in grade 8. ŌĆó The middle school standards are robust and provide a coherent and rich preparation for high school mathematics. 6-8 ŌĆó Students practice applying mathematical ways of thinking to real world issues and challenges; they prepare students to think and reason mathematically. 9-12 ŌĆó Set a rigorous definition of college and career readiness by helping students develop a depth of understanding and ability to apply mathematics to novel situations
- 11. Conceptual Understanding Procedural Skill
- 12. 6.EE.9- Use variables to represent two quantities in a real-world problem that change in relationship to one another; write an equation to express one quantity, thought of as the dependent variable, in terms of the other quantity, thought of as the independent variable. Analyze the relationship between the dependent and independent variables using graphs and tables, and relate these to the equation. 7.EE.4-Use variables to represent quantities in a real-world or mathematical problem, and construct simple equations and inequalities to solve problems by reasoning about the quantities. 8.F.4-Understand that a function is a rule that assigns to each input exactly one output. The graph of a function is the set of ordered pairs consisting of an input and the corresponding output. Compare properties of two functions each represented in a different way (algebraically, graphically, numerically in tables, or by verbal descriptions)
- 13. Essential Question: What can we learn about the circumference of a circle as a function of its diameter? Objective: The learner will recognize that the table, graph and rule assign a value to pi and that pi and that the slope equals pi Materials: rulers, cans or containers, paper, and markers Prerequisite skills: proportional reasoning, function concept
- 14. Use functions to model relationships between quantities. ’üĮ 8.F.4 Construct a function to model a linear relationship between two quantities. Determine the rate of change and initial value of the function from a description of a relationship or from two (x, y) values, including reading these from a table or from a graph. Interpret the rate of change and initial value of a linear function in terms of the situation it models, and in terms of its graph or a table of values
- 15. 1. Work in groups of 4 2. Each person is assigned a responsibility 3. Materials are located on one table, once youŌĆÖre finished return all materials Responsibilities- Time Manager, Reader, Materials Manager, Presenter/Writer
- 16. ’üĮ Make sense of the problems and persevere in solving them. ’üĮ Reason abstractly and quantitatively. ’üĮ Construct viable arguments and critique the reasoning of others. ’üĮ Model with mathematics. ’üĮ Use appropriate tools strategically. ’üĮ Attend to precision. ’üĮ Look for and make use of structure. ’üĮ Look for and express regularity in repeated reasoning.
- 17. John Van de Walle, ŌĆ£It is both a qualitative and quantitative processŌĆØ. Qualitative Quantitive Process Process relationships evaluate analysis is assigns based on value observations
- 18. Proportional Reasoning Algebra I 6th Grade Describe Conceptual Relationships 8th Grade 7th Grade Geometry Make Prove Theorems Analyze Connections Similarity
- 19. Preoperational- occurs between ages of 2-6 years. Students use symbolic thinking Concrete Operational-occurs between ages of 7-12 years. StudentsŌĆÖ thought processes become organized and integrated with one another. Logical processes become more developed and are able to handle more complex problems. Formal Operational -begins at 12 years and lasts into adulthood. Students develop the ability to think about abstract concepts.
- 20. ŌŚÅ Group the rectangles into three groups of four rectangles and an odd one out. ŌŚÅ Discuss reasons for groupings. ŌŚÅ Measure and record the sides of each rectangle, calculate ratios for short to long sides for each one. ŌŚÅ Draw a graph plotting length against width.
- 21. G-CO.12Make Geometric Constructions ’üĮ Make formal geometric constructions with a variety of tools and methods (compass and straightedge, string, reflective devices, paper folding, dynamic geometric software, etc.). ’üĮ Copying a segment; copying an angle; bisecting a segment; bisecting an angle; constructing perpendicular lines, including the perpendicular bisector of a line segment; and constructing a line parallel to a given line through a point not on the line. ’üĮ Construct an equilateral triangle, a square, and a regular hexagon inscribed in a circle.
- 22. ’üĮ 6.G.4-Represent three-dimensional figures using nets made up of rectangles and triangles, and use the nets to find the surface area of these figures. Apply these techniques in the context of solving real-world and mathematical problems. ’üĮ 7.G.6-Solve real-world and mathematical problems involving area, volume and surface area of two- and three-dimensional objects composed of triangles, quadrilaterals, polygons, cubes, and right prisms.
- 23. Essential Question: How can you measure how much cardboard it takes to make a net for a box? Objective: The learner will develop a definition for surface area Materials: rulers, blackline master, comic strip (AIMS), scissors, tape Prerequisite skills: area and counting centimeter grids to calculate area
- 24. ’üĮ Make sense of the problems and persevere in solving them. ’üĮ Reason abstractly and quantitatively. ’üĮ Construct viable arguments and critique the reasoning of others. ’üĮ Model with mathematics. ’üĮ Use appropriate tools strategically. ’üĮ Attend to precision. ’üĮ Look for and make use of structure. ’üĮ Look for and express regularity in repeated reasoning.
Editor's Notes
- #13: Refer to Function in Circles activitiy
- #18: Show Dinosaur World video http://www.ket.org/scalecity/dinosaurworld.html as the introduction to proportional reasoning
- #19: Why
- #20: Why is this important to take into consideration when planning how to present information and what activities to use for a lesson? How does this affect a studentsŌĆÖ ability to grasp mathematical concepts?
- #21: What criteria was established for assigning the rectangles to a group? What strategy did you use? How does this activity support proportional reasoning? Why is it important to construct a graph for the rectangles? What are some anticipated learning difficulties that a teacher would expect? How would you modify this activity for students who lack cognitive development in the area of proportional reasoning? What are the pre-requisite skills need for this activity?
- #22: Vertical alignment teach with the end in mind.
- #23: How do these 2 standards connect to the high school geometry standard?