Mathematics grade 10
Download as PPTX, PDF2 likes498 views
This document provides instructions on solving simultaneous equations in three main steps: 1) using elimination or substitution to remove one variable and solve for the other, 2) determining the intersection point of two graphs, and 3) working through two examples that apply these steps. The examples calculate two resistances given their sum and difference, and find the points where two equations for x^2 + y^2 and y = -3x - 5 intersect. References for further information are also included.
1 of 15
Download to read offline















Recommended
Inverse variation copy



Inverse variation copyshaminakhan
Ėý
This document defines inverse variation and provides examples of using inverse variation to solve problems. It gives the formula that if y is inversely proportional to x, then y = k/x, where k is a constant. It then works through several word problems that involve finding unknown values of x or y given one value and the inverse proportional relationship between the variables.Combined variation



Combined variationMartinGeraldine
Ėý
The document describes a problem involving combined variation, where the variable z varies jointly as w and x, and inversely as y. It gives the equation of variation as z = kwx/y, where k is the constant of variation. It solves for k when z = 100, w = 4, x = 5, and y = 15, finding that k = 75. Therefore, the equation of combined variation is z = 75wx/y. It then uses this to solve for z when w = 1, x = 5, and y = 3, finding that z = 125.Variation



VariationMARILOUMAGSALAY
Ėý
May this presentation could help you, the pictures here is not mine I get it from YouTube videos, I upload this ppt because
most the ppt here help me a lot in my teaching mathematics. This topics is different kinds variation direct variation, inverse variation, joint variation and combined variation. Differential equation and Laplace Transform



Differential equation and Laplace Transformsujathavvv
Ėý
The document discusses several topics in mathematics including:
1. Differential equations in the form of Ay" + Byâē + cy = g(t) and their homogeneous solutions.
2. Classifications of integrals including singular integrals which are found by eliminating arbitrary constants from an integral equation.
3. Solving Lagrange's linear equations by writing subsidiary equations and finding integrals to get the general integral solution in the form Ï(u,v)=0.
4. The Laplace transform of a function f(t), denoted by L{f(t)}, which is defined as the integral of f(t)e^-st from 0 to infinity if it exists. Some properties of the Laplace transform areDifferential equation



Differential equationMohanamalar8
Ėý
The document discusses several topics in mathematics including:
1. General forms of second order linear differential equations and homogeneous equations.
2. Classifications of integrals including singular integrals which are defined as the eliminant of arbitrary constants from an integral equation.
3. Solving linear partial differential equations using Lagrange's method of finding integrals to reduce solutions to arbitrary functions.
4. The definition and properties of the Laplace transform, including using the initial value theorem and final value theorem to find the original function from its Laplace transform. joint variation



joint variationrina valencia
Ėý
z = kxy
z = -12
z = kxy
z = -84
z = kxy
z = -21
4.
a. Combined means together as a whole.
b. Combined variation is when a quantity varies jointly with respect to the product of two or more variables.
c. The mathematical statement that represents combined variation is a = k(bc) where a varies jointly as b and c multiplied together.Pair of linear equation in two variable 



Pair of linear equation in two variable Vineet Mathur
Ėý
This document discusses linear equations in two variables. It defines a linear equation as an equation between two variables that forms a straight line when graphed. It then defines a linear equation in two variables as an equation with two variables, usually x and y, where the variables are multiplied by a number or added to another term. The document goes on to explain that a system of linear equations can have one solution, no solution, or infinitely many solutions depending on whether the lines intersect at one point, do not intersect, or coincide. It describes algebraic and graphical methods for solving systems of linear equations, focusing on substitution, elimination, and cross-multiplication algebraic methods.Direct Variation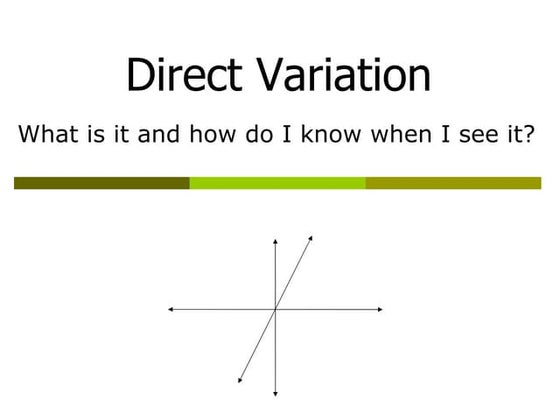



Direct VariationTeach5ch
Ėý
The document defines direct variation and provides examples of direct variation relationships. It explains that direct variation occurs when y varies directly with x, meaning y=kx where k is the constant of variation. As x increases or decreases, y also increases or decreases. The document provides examples of tables showing direct variation relationships and calculating the constant of variation k. It also shows how to use direct variation equations to solve word problems by finding the constant k and plugging values into y=kx. Finally, it discusses the graph of a direct variation relationship, noting it must pass through the origin.Solving problems involving direct variation



Solving problems involving direct variationMarzhie Cruz
Ėý
This document discusses direct variation and how to represent direct variation relationships using equations. It provides examples of how to write equations for direct variations between different variables such as cost and weight, circumference and diameter, water pressure and height. It also gives examples of writing direct variation equations from given values and using the equations to solve for unknown values when other values are given.Linear Equation In One Variable



Linear Equation In One VariablePooja M
Ėý
The document discusses linear expressions and equations. It provides examples of linear and nonlinear expressions, defines equations as statements of equality involving variables, and describes methods for solving different types of linear equations. These include balancing both sides of an equation, transposing terms between sides, solving equations with variables on one or both sides, and reducing equations to simpler or linear forms. Applications of linear equations to problems involving numbers, ages, and finances are also covered.Direct variation



Direct variationMarzhie Cruz
Ėý
The lesson is about introduction to direct variation. identify if the given table of values, graphs shows direct variation.Differential equation and Laplace transform



Differential equation and Laplace transformsujathavvv
Ėý
- Differential equations relate an unknown function and its derivatives, and are classified as ordinary (ODE) or partial (PDE) depending on the number of independent variables. Higher order equations can be reduced to systems of first order equations.
- Exact differential equations can be written as the total differential of a function, while non-exact equations may require an integrating factor to convert them to exact form.
- The general solution to a non-homogeneous second order differential equation is the sum of the complementary function (solution to the homogeneous equation) and a particular integral similar to the non-homogeneous term.PPTs FOR LINEAR EQUATIONS IN TWO VARIABLES BY RAMBABU SIRIPURAPU



PPTs FOR LINEAR EQUATIONS IN TWO VARIABLES BY RAMBABU SIRIPURAPURAMBABU SIRIPURAPU
Ėý
This document introduces linear equations in two variables. It defines a linear equation in two variables as an equation of the form ax + by + c = 0, where a, b, and c are real numbers and a and b are not both zero. It states that every solution to a linear equation in two variables is a point on the line representing the equation. The document also defines the general form for a pair of linear equations in two variables as a1x + b1y + c1 = 0 and a2x + b2y + c2 = 0, where a1, b1, c1, a2, b2, c2 are real numbers and a12 + b12 â 0,Pairs of linear equation in two variable by asim rajiv shandilya 10th a



Pairs of linear equation in two variable by asim rajiv shandilya 10th aasim1001
Ėý
This document provides an overview of pairs of linear equations in two variables. It discusses representing such equations graphically as two lines with possible solutions of unique intersection, no intersection, or overlapping lines. Algebraic methods for solving pairs of linear equations are presented, including substitution, elimination of a variable by making coefficients equal, and cross multiplication. Examples are provided to illustrate each method. The document also describes how to reduce equations not initially in the standard form for a pair of linear equations to that form so the equations can be solved using the described algebraic techniques.Kunal math linear equation with one variable



Kunal math linear equation with one variablekitukunal
Ėý
The document discusses linear equations and how to solve different types of linear equations. It provides examples of linear equations involving one variable, such as y=25x+100. It also discusses how to solve linear equations by performing the same operations to both sides of the equation, such as subtracting, adding, multiplying, or dividing terms, to isolate the variable. Examples are provided of solving equations involving one or two variables by transposing terms between the two sides of the equation.Daa linear recurrences



Daa linear recurrencesAtul Verma
Ėý
1) The document discusses solving linear recurrence relations, which are relations where each term is a linear combination of previous terms.
2) It provides methods for solving both homogeneous relations, where the right side is only previous terms, and non-homogeneous relations, where the right side also includes an additional term.
3) The key steps are finding the characteristic equation, which determines the possible solutions, then using the initial conditions to find the specific solution. Examples are worked through to demonstrate the process.Direct variation copy



Direct variation copyshaminakhan
Ėý
Direct variation describes the relationship between two quantities where they are in a constant ratio. If x is directly proportional to y, their relationship can be written as y = kx, where k is the constant of proportionality. Several examples are provided to demonstrate calculating the constant of proportionality given initial values of x and y, and then using the relationship to find corresponding values of y when given new values of x, and vice versa.Linear equations in 2 variables 



Linear equations in 2 variables Bhavyam Arora
Ėý
This document discusses linear equations. It defines linear equations as algebraic equations with terms that are constants or the product of constants and variables. Linear equations can have one or more variables. The document describes variables, constants, and examples of linear equations with one and two variables. It explains how to graph and solve systems of linear equations using graphical and algebraic methods like elimination and cross multiplication. Graphical methods involve plotting the lines defined by each equation and finding their point(s) of intersection. Algebraic methods eliminate variables to solve for the remaining ones.Polynomials And Linear Equation of Two Variables



Polynomials And Linear Equation of Two VariablesAnkur Patel
Ėý
A complete description of polynomials and also various methods to solve the Linear equation of two variables by substitution, cross multiplication and elimination methods.
For polynomials it also contains the description of monomials, binomials etc.8.2 Equations W Two Variables



8.2 Equations W Two VariablesJessca Lundin
Ėý
This document provides information about equations with two variables including:
- Examples of solving for y when given a value for x
- Real-life examples modeling temperature at different elevations
- How to graph linear equations by making a table of values and plotting points
- The vertical line test to determine if a relation is a functionUnit 4 hw 7 - direct variation & linear equation give 2 points



Unit 4 hw 7 - direct variation & linear equation give 2 pointsLori Rapp
Ėý
This document discusses direct variation, which is a linear equation that passes through the origin. It defines direct variation as y=kx, where k is the constant of variation. It provides examples of graphs that do and do not represent direct variations. It also shows step-by-step processes for finding the direct variation equation from two points, and for solving a direct variation problem when given a point and asked to find the corresponding y-value for a different x-value.Linear equtions with one variable



Linear equtions with one variableANKIT SAHOO
Ėý
The document discusses equations and how to solve them. It defines an equation as a statement where two algebraic expressions are equal. It also defines a linear equation as one involving only one variable.
It then lists the four properties of equations: adding/subtracting the same quantity to both sides, multiplying/dividing both sides by the same quantity.
Next, it provides examples of how to solve different types of equations (those involving addition, subtraction, multiplication, or division of the variable) using both the traditional method of operations and the shortcut method of transposing terms.
Finally, it gives examples of solving equations with variables on both sides, word problems involving equations, and equations from applied contexts like age.Inverse Variation



Inverse VariationJoseph Nilo
Ėý
The document discusses different types of variations:
1) Direct variation results in a straight line graph, while direct square variation results in a parabolic graph.
2) Inverse variation means that as one variable increases, the other decreases, maintaining a constant product. The graph of an inverse variation is a hyperbola.
3) Examples show inverse variations between variables like pressure and volume of a gas, or jobs completed and number of workers.
4) Quiz questions test understanding of direct, inverse, and their equation representations.PROJECT (PPT) ON PAIR OF LINEAR EQUATIONS IN TWO VARIABLES - CLASS 10



PROJECT (PPT) ON PAIR OF LINEAR EQUATIONS IN TWO VARIABLES - CLASS 10mayank78610
Ėý
THIS A PROJECT BEING MADE BY INFORMATION COLLECTED FROM CLASS 10 MATHS NCERT BOOK.
THANK YOU FOR SEEING MY PROJECT ... I THINK THIS MIGHT HELP YOU IN YOUR HOLIDAY HOMEWORK PROJECTS .Chapter 5 Direct Variation



Chapter 5 Direct VariationIinternational Program School
Ėý
This document discusses direct variation and how to identify, write equations for, solve, and graph direct variations. It provides examples of identifying direct variations from equations and ordered pairs by checking if the equations are in the form y=kx or if the ratio k is the same for each pair. It also gives examples of writing and solving direct variation equations using the constant k or proportions, and graphing direct variations by choosing x-values and generating ordered pairs.5.3 Direct Variation C



5.3 Direct Variation Cvmonacelli
Ėý
The document discusses direct variation equations and examples of finding the constant of variation and slope from equations relating two variables. It provides examples of identifying the constant of variation from equations, finding the slope, and writing direct variation equations. It also includes an example of graphing a direct variation equation.Linear equations in two variables



Linear equations in two variablesjulienorman80065
Ėý
1) The document discusses finding solutions to linear equations in two variables by using tables and plotting points on a coordinate plane.
2) It provides an example of writing an equation to represent the number of two-point and three-point baskets scored in a basketball game.
3) The key strategy explained is to fix a value for one variable (x or y), then solve the equation for the other variable to obtain an ordered pair solution (x, y).LINEAR DIFFERENTIAL EQUATION & BERNOULLI`S EQUATION



LINEAR DIFFERENTIAL EQUATION & BERNOULLI`S EQUATIONTouhidul Shawan
Ėý
This slide is about LINEAR DIFFERENTIAL EQUATION & BERNOULLI`S EQUATION. It is one of the important parts of mathematics. This slide will help you to understand the basis of these two parts one Linear Differential Equation and other Bernoulli`s equation. MIT Math Syllabus 10-3 Lesson 6: Equations



MIT Math Syllabus 10-3 Lesson 6: EquationsLawrence De Vera
Ėý
This document provides information about equations, including definitions, properties, and steps to solve different types of equations. It defines an equation as a statement about the equality of two expressions. Equations can be solved to find all values that satisfy the equation. The key properties of equality, including addition/subtraction and multiplication/division properties, allow equivalent equations to be formed in order to solve equations. The document discusses linear equations, absolute value equations, formulas, and using equations to model real-world situations.More Related Content
What's hot (20)
Solving problems involving direct variation



Solving problems involving direct variationMarzhie Cruz
Ėý
This document discusses direct variation and how to represent direct variation relationships using equations. It provides examples of how to write equations for direct variations between different variables such as cost and weight, circumference and diameter, water pressure and height. It also gives examples of writing direct variation equations from given values and using the equations to solve for unknown values when other values are given.Linear Equation In One Variable



Linear Equation In One VariablePooja M
Ėý
The document discusses linear expressions and equations. It provides examples of linear and nonlinear expressions, defines equations as statements of equality involving variables, and describes methods for solving different types of linear equations. These include balancing both sides of an equation, transposing terms between sides, solving equations with variables on one or both sides, and reducing equations to simpler or linear forms. Applications of linear equations to problems involving numbers, ages, and finances are also covered.Direct variation



Direct variationMarzhie Cruz
Ėý
The lesson is about introduction to direct variation. identify if the given table of values, graphs shows direct variation.Differential equation and Laplace transform



Differential equation and Laplace transformsujathavvv
Ėý
- Differential equations relate an unknown function and its derivatives, and are classified as ordinary (ODE) or partial (PDE) depending on the number of independent variables. Higher order equations can be reduced to systems of first order equations.
- Exact differential equations can be written as the total differential of a function, while non-exact equations may require an integrating factor to convert them to exact form.
- The general solution to a non-homogeneous second order differential equation is the sum of the complementary function (solution to the homogeneous equation) and a particular integral similar to the non-homogeneous term.PPTs FOR LINEAR EQUATIONS IN TWO VARIABLES BY RAMBABU SIRIPURAPU



PPTs FOR LINEAR EQUATIONS IN TWO VARIABLES BY RAMBABU SIRIPURAPURAMBABU SIRIPURAPU
Ėý
This document introduces linear equations in two variables. It defines a linear equation in two variables as an equation of the form ax + by + c = 0, where a, b, and c are real numbers and a and b are not both zero. It states that every solution to a linear equation in two variables is a point on the line representing the equation. The document also defines the general form for a pair of linear equations in two variables as a1x + b1y + c1 = 0 and a2x + b2y + c2 = 0, where a1, b1, c1, a2, b2, c2 are real numbers and a12 + b12 â 0,Pairs of linear equation in two variable by asim rajiv shandilya 10th a



Pairs of linear equation in two variable by asim rajiv shandilya 10th aasim1001
Ėý
This document provides an overview of pairs of linear equations in two variables. It discusses representing such equations graphically as two lines with possible solutions of unique intersection, no intersection, or overlapping lines. Algebraic methods for solving pairs of linear equations are presented, including substitution, elimination of a variable by making coefficients equal, and cross multiplication. Examples are provided to illustrate each method. The document also describes how to reduce equations not initially in the standard form for a pair of linear equations to that form so the equations can be solved using the described algebraic techniques.Kunal math linear equation with one variable



Kunal math linear equation with one variablekitukunal
Ėý
The document discusses linear equations and how to solve different types of linear equations. It provides examples of linear equations involving one variable, such as y=25x+100. It also discusses how to solve linear equations by performing the same operations to both sides of the equation, such as subtracting, adding, multiplying, or dividing terms, to isolate the variable. Examples are provided of solving equations involving one or two variables by transposing terms between the two sides of the equation.Daa linear recurrences



Daa linear recurrencesAtul Verma
Ėý
1) The document discusses solving linear recurrence relations, which are relations where each term is a linear combination of previous terms.
2) It provides methods for solving both homogeneous relations, where the right side is only previous terms, and non-homogeneous relations, where the right side also includes an additional term.
3) The key steps are finding the characteristic equation, which determines the possible solutions, then using the initial conditions to find the specific solution. Examples are worked through to demonstrate the process.Direct variation copy



Direct variation copyshaminakhan
Ėý
Direct variation describes the relationship between two quantities where they are in a constant ratio. If x is directly proportional to y, their relationship can be written as y = kx, where k is the constant of proportionality. Several examples are provided to demonstrate calculating the constant of proportionality given initial values of x and y, and then using the relationship to find corresponding values of y when given new values of x, and vice versa.Linear equations in 2 variables 



Linear equations in 2 variables Bhavyam Arora
Ėý
This document discusses linear equations. It defines linear equations as algebraic equations with terms that are constants or the product of constants and variables. Linear equations can have one or more variables. The document describes variables, constants, and examples of linear equations with one and two variables. It explains how to graph and solve systems of linear equations using graphical and algebraic methods like elimination and cross multiplication. Graphical methods involve plotting the lines defined by each equation and finding their point(s) of intersection. Algebraic methods eliminate variables to solve for the remaining ones.Polynomials And Linear Equation of Two Variables



Polynomials And Linear Equation of Two VariablesAnkur Patel
Ėý
A complete description of polynomials and also various methods to solve the Linear equation of two variables by substitution, cross multiplication and elimination methods.
For polynomials it also contains the description of monomials, binomials etc.8.2 Equations W Two Variables



8.2 Equations W Two VariablesJessca Lundin
Ėý
This document provides information about equations with two variables including:
- Examples of solving for y when given a value for x
- Real-life examples modeling temperature at different elevations
- How to graph linear equations by making a table of values and plotting points
- The vertical line test to determine if a relation is a functionUnit 4 hw 7 - direct variation & linear equation give 2 points



Unit 4 hw 7 - direct variation & linear equation give 2 pointsLori Rapp
Ėý
This document discusses direct variation, which is a linear equation that passes through the origin. It defines direct variation as y=kx, where k is the constant of variation. It provides examples of graphs that do and do not represent direct variations. It also shows step-by-step processes for finding the direct variation equation from two points, and for solving a direct variation problem when given a point and asked to find the corresponding y-value for a different x-value.Linear equtions with one variable



Linear equtions with one variableANKIT SAHOO
Ėý
The document discusses equations and how to solve them. It defines an equation as a statement where two algebraic expressions are equal. It also defines a linear equation as one involving only one variable.
It then lists the four properties of equations: adding/subtracting the same quantity to both sides, multiplying/dividing both sides by the same quantity.
Next, it provides examples of how to solve different types of equations (those involving addition, subtraction, multiplication, or division of the variable) using both the traditional method of operations and the shortcut method of transposing terms.
Finally, it gives examples of solving equations with variables on both sides, word problems involving equations, and equations from applied contexts like age.Inverse Variation



Inverse VariationJoseph Nilo
Ėý
The document discusses different types of variations:
1) Direct variation results in a straight line graph, while direct square variation results in a parabolic graph.
2) Inverse variation means that as one variable increases, the other decreases, maintaining a constant product. The graph of an inverse variation is a hyperbola.
3) Examples show inverse variations between variables like pressure and volume of a gas, or jobs completed and number of workers.
4) Quiz questions test understanding of direct, inverse, and their equation representations.PROJECT (PPT) ON PAIR OF LINEAR EQUATIONS IN TWO VARIABLES - CLASS 10



PROJECT (PPT) ON PAIR OF LINEAR EQUATIONS IN TWO VARIABLES - CLASS 10mayank78610
Ėý
THIS A PROJECT BEING MADE BY INFORMATION COLLECTED FROM CLASS 10 MATHS NCERT BOOK.
THANK YOU FOR SEEING MY PROJECT ... I THINK THIS MIGHT HELP YOU IN YOUR HOLIDAY HOMEWORK PROJECTS .Chapter 5 Direct Variation



Chapter 5 Direct VariationIinternational Program School
Ėý
This document discusses direct variation and how to identify, write equations for, solve, and graph direct variations. It provides examples of identifying direct variations from equations and ordered pairs by checking if the equations are in the form y=kx or if the ratio k is the same for each pair. It also gives examples of writing and solving direct variation equations using the constant k or proportions, and graphing direct variations by choosing x-values and generating ordered pairs.5.3 Direct Variation C



5.3 Direct Variation Cvmonacelli
Ėý
The document discusses direct variation equations and examples of finding the constant of variation and slope from equations relating two variables. It provides examples of identifying the constant of variation from equations, finding the slope, and writing direct variation equations. It also includes an example of graphing a direct variation equation.Linear equations in two variables



Linear equations in two variablesjulienorman80065
Ėý
1) The document discusses finding solutions to linear equations in two variables by using tables and plotting points on a coordinate plane.
2) It provides an example of writing an equation to represent the number of two-point and three-point baskets scored in a basketball game.
3) The key strategy explained is to fix a value for one variable (x or y), then solve the equation for the other variable to obtain an ordered pair solution (x, y).LINEAR DIFFERENTIAL EQUATION & BERNOULLI`S EQUATION



LINEAR DIFFERENTIAL EQUATION & BERNOULLI`S EQUATIONTouhidul Shawan
Ėý
This slide is about LINEAR DIFFERENTIAL EQUATION & BERNOULLI`S EQUATION. It is one of the important parts of mathematics. This slide will help you to understand the basis of these two parts one Linear Differential Equation and other Bernoulli`s equation. Similar to Mathematics grade 10 (20)
MIT Math Syllabus 10-3 Lesson 6: Equations



MIT Math Syllabus 10-3 Lesson 6: EquationsLawrence De Vera
Ėý
This document provides information about equations, including definitions, properties, and steps to solve different types of equations. It defines an equation as a statement about the equality of two expressions. Equations can be solved to find all values that satisfy the equation. The key properties of equality, including addition/subtraction and multiplication/division properties, allow equivalent equations to be formed in order to solve equations. The document discusses linear equations, absolute value equations, formulas, and using equations to model real-world situations.Linear, quardratic equations



Linear, quardratic equationsRekhaChoudhary24
Ėý
This document provides an introduction to different types of equations including linear equations, simultaneous equations, and quadratic equations. It defines an equation as a statement of equality between two quantities. Linear equations are those where the highest power of the unknown is one. Simultaneous equations contain two or more unknowns and can be solved using substitution or row operations. Quadratic equations contain terms with powers of the unknown up to two and can be solved using factorization, completing the square, or the quadratic formula. Examples are provided for solving each type of equation. The objectives and end questions review solving these different equation types.Equation and Expression_Math foe MBA pro



Equation and Expression_Math foe MBA proTonmoyKabiraj
Ėý
This document discusses equations and expressions. It defines equations as mathematical statements containing two algebraic expressions separated by an equal sign. Equations can be solved to find the value of an unknown variable. The document also discusses the different parts of an equation, how to solve equations by performing the same operations to both sides, and types of equations such as linear, quadratic and cubic equations. It provides examples of solving linear equations in one and two variables.Theory of Equation



Theory of EquationSOMASUNDARAM T
Ėý
1. The document provides an overview of the key concepts in the Theory of Equations unit, including types of equations, methods for solving different types of equations, and properties of roots.
2. It discusses linear equations, simultaneous equations, quadratic equations and their solving methods like elimination, substitution, and factorization.
3. Examples of equation problems from commercial applications are also presented, involving linear, simultaneous and quadratic equations. Worked examples and practice problems are provided for each topic.Maths



Mathsrahul4567567
Ėý
This document discusses linear equations in two variables. It defines linear equations in two variables as equations of the form ax + by = c, where a, b, and c are real numbers and a and b are not both zero. It explains that the graph of any linear equation in two variables is a straight line. It also categorizes different types of systems of linear equations based on the relationship between the lines: intersecting lines have a unique solution; coincident lines have an infinite number of solutions; and parallel lines have no solution. Methods for solving systems of linear equations like substitution, elimination, and graphing are also covered.Ppt spldv kelas viii



Ppt spldv kelas viiiMartiwiFarisa
Ėý
Sistem persamaan linear dua variabel adalah suatu persamaan yang memiliki dua persamaan dan juga dua variabel. Hasil penyelesaian SPLDV adalah berupa titik potong.Regression.pptx



Regression.pptxShivakumar B N
Ėý
Regression analysis is a mathematical measure of the average relationship between two or more variables in terms of the original units of the data.
In regression analysis there are two types of variables. The variable whose value is influenced or is to be predicted is called dependent variable and the variable which influences the values or is used for prediction, is called independent variable.
In regression analysis independent variable is also known as regressor or predictor or explanatory variable while the dependent variable is also known as regressed or explained variable.Calculus ebook



Calculus ebookAllan Mabele Nambafu
Ėý
1. The document discusses differentiation rules including the product rule, quotient rule, chain rule, and implicit differentiation. Examples are provided to illustrate how to use each rule to take derivatives.
2. Trigonometric differentiation rules are also covered, including that the derivative of sine is cosine and the derivative of cosine is the negative of sine. Exponential and logarithmic differentiation formulas are defined.
3. The document also discusses parametric differentiation and provides examples of taking derivatives of parametric equations.Group No 05, calculus.pptx



Group No 05, calculus.pptxEmonKundu
Ėý
1) The document introduces concepts of differential calculus including derivatives, limits, continuity, and fundamental rules of taking derivatives.
2) It provides examples of calculating derivatives using notations like delta f, limits, and various derivative rules including the power rule, product rule, and quotient rule.
3) Methods for finding local maxima and minima are discussed, including using the first derivative test and analyzing stationary points where the first derivative is zero based on whether the derivative is increasing or decreasing on both sides.Class 3.pdf



Class 3.pdfShahidaRashid2125518
Ėý
This document discusses solving simultaneous linear equations through algebraic and graphical methods. It covers:
- Algebraic methods like substitution and elimination to solve 2 equations with 2 unknowns.
- Graphing methods to find the point where two lines intersect, representing the solution.
- Conditions where equations have a unique solution, no solution, or infinitely many solutions.
- Extended examples are provided to demonstrate solving 2 and 3 equations with algebraic elimination.Solving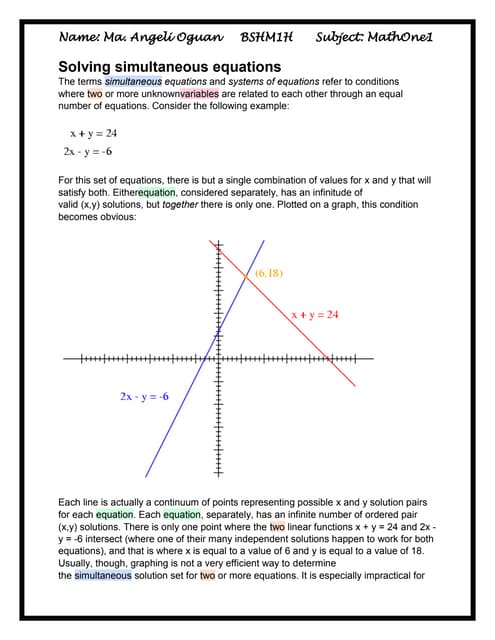



SolvingSozeth Delos Angeles
Ėý
The document discusses the elimination method for solving simultaneous equations. It involves adding or subtracting two equations to eliminate one of the variables. This leaves an equation with only one variable that can then be solved for. Examples are provided to demonstrate how to eliminate variables by adding or subtracting equations. It notes that sometimes equations need to be multiplied by a number first to get equal terms that can cancel out before elimination can occur. The goal is to reduce the simultaneous equations down to one equation with one variable that can then be solved.Consistency of linear equations in two and three variables



Consistency of linear equations in two and three variablesAamlan Saswat Mishra
Ėý
This document discusses solving systems of linear equations with two or three variables. It explains that a system can have one solution, infinitely many solutions, or no solution. For two variables, the solutions are where lines intersect (one solution), coincide (infinitely many), or are parallel (no solution). For three variables, the solutions are where planes intersect (one point), lie on a line (infinitely many), or do not intersect (no solution). It demonstrates solving systems using substitution, elimination, and matrix methods, and discusses cases where a system has infinitely many or no solutions.2.6 Other Types of Equations



2.6 Other Types of Equationssmiller5
Ėý
* Solve equations involving rational exponents
* Solve equations using factoring
* Solve equations with radicals and check the solutions
* Solve absolute value equations
* Solve other types of equations
Linear equations



Linear equationscriss ch
Ėý
The document discusses linear equations, which involve variables raised to the first power. It provides examples of linear equations with one, two, and three variables. Linear equations can be used to solve real-world problems involving costs. The document also discusses representing linear equations graphically and solving systems of linear equations using various methods like substitution. Linear inequalities are also introduced, which involve inequality signs rather than equals signs. An example problem demonstrates solving a linear inequality for the variable.Linear equations



Linear equationscriss ch
Ėý
The document discusses linear equations and their applications. It defines linear equations as equations where variables have a degree of one and do not involve products or roots of variables. Linear equations can be used to solve real-life problems involving costs and quantities. The document discusses different forms of linear equations with one, two, or three variables. It also discusses solving systems of linear equations using various methods like substitution. Graphs of linear equations are shown to be lines or points on a number line. Methods to solve and graph linear equations and inequalities are presented..



.leoscotch
Ėý
This document provides information about solving absolute value equations and inequalities, as well as quadratic equations. It discusses:
1) To solve absolute value equations, you must divide the equation into two equations by treating the expression inside the absolute value bars as both positive and negative.
2) For inequalities, the direction of the inequality sign must be reversed when multiplying or dividing both sides by a negative number.
3) Quadratic equations can be solved by factoring if possible, or using the quadratic formula. The discriminant determines the number of real roots.Linear equations Class 10 by aryan kathuria



Linear equations Class 10 by aryan kathuriaDhiraj Singh
Ėý
This document discusses linear equations and methods to solve systems of linear equations. It defines a linear equation as an equation that can be written in the form ax + by + c = 0, where a, b, and c are real numbers and a and b are not equal to 0. Systems of linear equations can have unique solutions, infinite solutions, or no solutions depending on whether the lines intersect, are coincident, or are parallel. The document describes graphical and algebraic methods to solve systems, including elimination, substitution, and cross-multiplication methods. It provides examples of using each algebraic method to solve systems of two linear equations with two unknowns.Helmholtz equation (Motivations and Solutions)



Helmholtz equation (Motivations and Solutions)Hassaan Saleem
Ėý
Solutions of Helmholtz equation in cartesian, cylindrical and spherical coordinates are discussed and the applications to the problem of a quantum mechanical particle in a cubical box is discussed.CALCULUS 2.pptx



CALCULUS 2.pptxShienaMaeIndac
Ėý
This document provides information about Calculus 2, including lessons on indeterminate forms, Rolle's theorem, the mean value theorem, and differentiation of transcendental functions. It defines Rolle's theorem and the mean value theorem, provides examples of applying each, and discusses how Rolle's theorem can be used to find the value of c. It also defines inverse trigonometric functions and their derivatives. The document is for MATH 09 Calculus 2 and includes exercises for students to practice applying the theorems.Recently uploaded (20)
Functional Muscle Testing of Facial Muscles.pdf



Functional Muscle Testing of Facial Muscles.pdfSamarHosni3
Ėý
Functional Muscle Testing of Facial Muscles.pdfHow to create security group category in Odoo 17



How to create security group category in Odoo 17Celine George
Ėý
This slide will represent the creation of security group category in odoo 17. Security groups are essential for managing user access and permissions across different modules. Creating a security group category helps to organize related user groups and streamline permission settings within a specific module or functionality.Intellectual Honesty & Research Integrity.pptx



Intellectual Honesty & Research Integrity.pptxNidhiSharma495177
Ėý
Research Publication & Ethics contains a chapter on Intellectual Honesty and Research Integrity.
Different case studies of intellectual dishonesty and integrity were discussed.Odoo 18 Accounting Access Rights - Odoo 18 šÝšÝßĢs



Odoo 18 Accounting Access Rights - Odoo 18 šÝšÝßĢsCeline George
Ėý
In this slide, weâll discuss on accounting access rights in odoo 18. To ensure data security and maintain confidentiality, Odoo provides a robust access rights system that allows administrators to control who can access and modify accounting data. Mastering Soft Tissue Therapy & Sports Taping



Mastering Soft Tissue Therapy & Sports TapingKusal Goonewardena
Ėý
Mastering Soft Tissue Therapy & Sports Taping: Pathway to Sports Medicine Excellence
This presentation was delivered in Colombo, Sri Lanka, at the Institute of Sports Medicine to an audience of sports physiotherapists, exercise scientists, athletic trainers, and healthcare professionals. Led by Kusal Goonewardena (PhD Candidate - Muscle Fatigue, APA Titled Sports & Exercise Physiotherapist) and Gayath Jayasinghe (Sports Scientist), the session provided comprehensive training on soft tissue assessment, treatment techniques, and essential sports taping methods.
Key topics covered:
â
Soft Tissue Therapy â The science behind muscle, fascia, and joint assessment for optimal treatment outcomes.
â
Sports Taping Techniques â Practical applications for injury prevention and rehabilitation, including ankle, knee, shoulder, thoracic, and cervical spine taping.
â
Sports Trainer Level 1 Course by Sports Medicine Australia â A gateway to professional development, career opportunities, and working in Australia.
This training mirrors the Elite Akademy Sports Medicine standards, ensuring evidence-based approaches to injury management and athlete care.
If you are a sports professional looking to enhance your clinical skills and open doors to global opportunities, this presentation is for you.Chapter 2. Strategic Management: Corporate Governance.pdf



Chapter 2. Strategic Management: Corporate Governance.pdfRommel Regala
Ėý
This course provides students with a comprehensive understanding of strategic management principles, frameworks, and applications in business. It explores strategic planning, environmental analysis, corporate governance, business ethics, and sustainability. The course integrates Sustainable Development Goals (SDGs) to enhance global and ethical perspectives in decision-making.RRB ALP CBT 2 RAC Question Paper MCQ (Railway Assistant Loco Pilot)



RRB ALP CBT 2 RAC Question Paper MCQ (Railway Assistant Loco Pilot)SONU HEETSON
Ėý
RRB ALP CBT 2 RAC Question Paper MCQ PDF Free Download. Railway Assistant Loco Pilot Mechanic Refrigeration and Air Conditioning Important Questions.Meeting the needs of modern students?, Selina McCoy



Meeting the needs of modern students?, Selina McCoyEconomic and Social Research Institute
Ėý
NAPD Annual Symposium
âEquity in our Schools: Does the system deliver for all young people?âRRB ALP CBT 2 Mechanic Motor Vehicle Question Paper (MMV Exam MCQ)



RRB ALP CBT 2 Mechanic Motor Vehicle Question Paper (MMV Exam MCQ)SONU HEETSON
Ėý
RRB ALP CBT 2 Mechanic Motor Vehicle Question Paper. MMV MCQ PDF Free Download for Railway Assistant Loco Pilot Exam.Báŧ TEST KIáŧM TRA GIáŧŪA KÃ 2 - TIášūNG ANH 10,11,12 - CHUášĻN FORM 2025 - GLOBAL SU...



Báŧ TEST KIáŧM TRA GIáŧŪA KÃ 2 - TIášūNG ANH 10,11,12 - CHUášĻN FORM 2025 - GLOBAL SU...Nguyen Thanh Tu Collection
Ėý
https://app.box.com/s/ij1ty3vm7el9i4qfrr41o756xycbahmgEntity Framework Interview Questions PDF By ScholarHat



Entity Framework Interview Questions PDF By ScholarHatScholarhat
Ėý
Entity Framework Interview Questions PDF By ScholarHatBáŧ TEST KIáŧM TRA GIáŧŪA KÃ 2 - TIášūNG ANH 10,11,12 - CHUášĻN FORM 2025 - GLOBAL SU...



Báŧ TEST KIáŧM TRA GIáŧŪA KÃ 2 - TIášūNG ANH 10,11,12 - CHUášĻN FORM 2025 - GLOBAL SU...Nguyen Thanh Tu Collection
Ėý
Mathematics grade 10
- 2. To solve two simultaneous equations means to use both equations together to find one value for each unkown so that these values satisfy both equations.
- 3. Steps to solve a quadratic equation. ïĩMove all terms to the LHS leaving only a zero on the RHS ïĩFactorise the LSH ïĩUse the zero-factor principle to find the values of variables
- 4. Methods to solve simultaneous equations. ïĩBy elimination of one variable ïĩBy substituting ïĩBy determining the intersection point of two graphs.
- 5. Example. ïĩThe sum of two resistance is 14 and their difference is 6. Determine the two resistances.
- 6. Solution X + y =14....(1) X-y =6 2x=20 x=10
- 7. ïĩSubstitute x =10 into ..... (1) 10 + y = 14 y=14-10 y=4 The resistance are 10 and 4
- 8. Example 2 ïĩ X^2 +Y^2= 25 ïĩ Y= -3X â 5 Solution X^2 + y^2 =25..... (1) Y= -3xâ5...... (2)
- 11. Substitute x=-3xâ5 Y=-3 (-3)â5 Y=4 (0,5) or (-3,4)
- 12. References Larson R, (2014).Precalculus 9th edition, The Pennylvania state University. Cengage Learning.
- 13. Example.










