Maths P.P.T. Connectives
- 2. The words and phrases to form compound statements are called connectives. There are five basic connectives :- 1) Conjunction 2) Disjunction 3) Negation 4) Implication or Conditional 5) Equivalence or Biconditional
- 3. Truth Functions âĒ Declarative sentences (statements) are either true or false but not both. They cannot be neither. âĒ Whether a sentence is true or false determines its truth value. âĒ Functions take input values to unique output values . That is, the input values determine the output values. âĒ There are some ways of combining sentences into longer ones so that the truth value of the longer sentence is determined by the truth value of the parts that were combined to form it. âĒ So, weâll call the connectives , that combine sentences in this way that they form truth functions.
- 4. 1) CONJUNCTION ï Symbol used :- ï Connective word :- and ï Its symbolic form :- p q ï âAndâ is often a truth functional connective . Inserting âandâ between two statements gives a longer sentence , the truth of which is determined by the truth of the parts. ï If p and q are both true then the longer sentence is true. If either of p or q is false ï ï
- 5. p : John passes. h : John is happy ï This symbol replaces the word âANDâ John passes AND John is happy ïp h
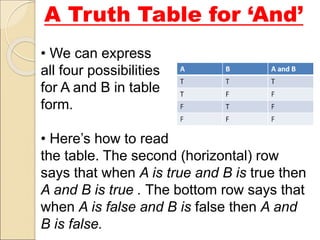
- 6. âĒ We can express all four possibilities for A and B in table form. âĒ Hereâs how to read the table. The second (horizontal) row says that when A is true and B is true then A and B is true . The bottom row says that when A is false and B is false then A and B is false. A Truth Table for âAndâ
- 7. 2) DISJUNCTION ï Symbol used :- V ï Connective word :- or ï Its symbolic form :- p V q Examples :- ïEither Lenny or Manny left for Bermuda. (L=Lenny left for Bermuda. M=Manny left for Bermuda.) Translation : L V M
- 8. Truth Table for Disjunction âĒ The four possibilities For sentences A and B are represented by the left two (vertical) columns. âĒ The top row of Ts and Fs is the possibility where A is true and B is true. On that possibility âA V Bâ is true. âĒ The bottom row is the possibility where A and B are both false. In that case âA V Bâ is also false. âĒ Disjunction differs from conjunction on the middle two rows.
- 9. 3) NEGATION ï Symbol used :- ~ ï Connective word :- not ï Its symbolic form :- ~ p ï Prefixing a statement with âit is not the case thatâ flips the truth value. Examples :- ï Manny left but Lenny did not leave. (L=Lenny left for Bermuda. M=Manny left for Bermuda.) Translation : M ~Lï
- 10. Truth Table for Negation âĒ The symbol to represent that truth function is â ~ â. The symbol is called âtildeâ or just âsquiggleâ. âĒ Unlike the other connectives, tilde doesnât connect two sentences. It just flips the value of a single sentence.
- 11. s : John studies. John does NOT study: s This symbol negates the statement it precedes ~ ~ Example :-
- 12. 4) IMPLICATION ( or CONDITIONAL ) ï Symbol used :- ï Connective word :- if........then ï Its symbolic form :- p q ï Some uses of âif..thenâĶâ are truth functional and some are not . ï Consider: If you whistle loudly then the dog will come. Thereâs really just one scenario that shows the sentence to be false: whistle loudly and have the dog not come. If you whistle and the dog comes then the sentence was true. If you donât whistle then no matter whether the dog comes or not, you didnât show the ïŪ ïŪ
- 13. s : John studies. p : John passes. ïŪ This symbol replaces the connective âif âĶ thenâ IF John studies THEN John passes. ïŪs p Example :-
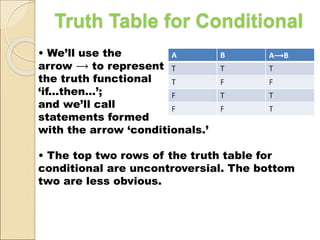
- 14. Truth Table for Conditional âĒ Weâll use the arrow âķ to represent the truth functional âif...thenâĶâ; and weâll call statements formed with the arrow âconditionals.â âĒ The top two rows of the truth table for conditional are uncontroversial. The bottom two are less obvious.
- 15. Order Matters âĒ Notice on the table that the order of A and B matter. A true and B false yields a different value than A false and B true. So, unlike conjunction and disjunction where order doesnât matter, we have a different names for the different parts of the conditional. âĒ For A âķ B, A is called the âantecedentâ and B is called the âconsequentâ. âĒ There are many English expressions that can be translated as conditionals. The trick to symbolizing them correctly is to identify the antecedent and the consequent.
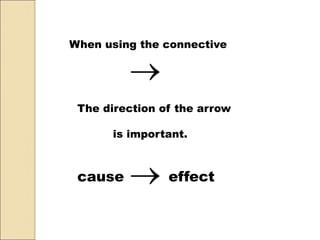
- 16. When using the connective ïŪ The direction of the arrow is important. ïŪcause effect
- 17. 6) EQUIVALENCE ( or BICONDITIONAL ) ï Symbol used :- ï Connective word :- if and only if ï Its symbolic form :- p q ï If we say â A if B and A only if B â or in other words âA if and only if Bâ we could translate that as â(BâķA)&(AâķB)â.Weâll use the double arrow â· (or the triple bar ) as an abbreviation for that. Also, weâll call sentences formed by using the double arrow âbiconditionalsâ. ï Sometimes you see âiffâ between two sentences. Itâs not a typo. Itâs an abbreviation for âif and only if.â So âA iff Bâ would be translated as ïŦ ïŦ
- 18. s : John studies. h : John is happy ïŦ This symbol replaces the words âif and only ifâ John is happy IF AND ONLY IF John studies. ïŦh s Example :-
- 19. Truth Table for Biconditional âĒ Think of the biconditional as saying that two sentences have matching truth value. The longer sentence is true when both parts are true or when both parts are false. âĒ Notice that order doesnât matter ; so we donât have special names for the letter that comes first. Unlike regular conditional, A â· B is equivalent to Bâ·A. âĒ The sentence âAâ·B âis just an abbreviation for the more complicated sentence â(BâķA)&(AâķB)â.
- 20. John is happy ONLY IF he studies. John is happy IF he studies. John is happy IF AND ONLY IF he studies. ïŪ ïŽ ïŽïŪ Example :-